Câu hỏi:
23/07/2024 1,029
Cho các số dương a, b thay đổi luôn thỏa mãn b > a > 1. Tìm giá trị nhỏ nhất của biểu thức P=logab+1logab−1
A. 2√2
B. 134
C. 3
D. 3√2
Trả lời:
Giải bởi Vietjack
Chọn D
Đặt logab=t. Do 1<a<b⇒logab>1⇒t>1. Áp dụng BĐT Co-si cho 2 số dương t−1;1t−1
Ta có: P=t+1t−1=(t−1+1t−1)+1≥2√(t−1).1t−1+1=3.
Dấu ''='' xảy ra ⇔t−1=1t−1⇔t=2. Vậy GTNN của P bằng 3 khi b=a2..
Chọn D
Đặt logab=t. Do 1<a<b⇒logab>1⇒t>1. Áp dụng BĐT Co-si cho 2 số dương t−1;1t−1
Ta có: P=t+1t−1=(t−1+1t−1)+1≥2√(t−1).1t−1+1=3.
Dấu ''='' xảy ra ⇔t−1=1t−1⇔t=2. Vậy GTNN của P bằng 3 khi b=a2..
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên như sau
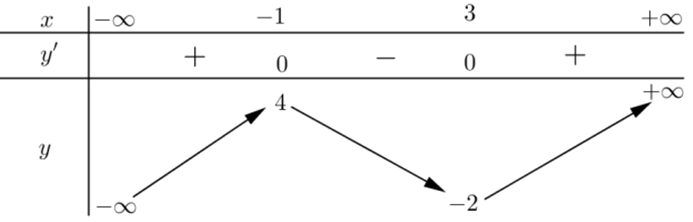
Hỏi phương trình f(x) = 3 có bao nhiêu nghiệm?
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên như sau
Hỏi phương trình f(x) = 3 có bao nhiêu nghiệm?
Câu 2:
Tính bán kính mặt cầu ngoại tiếp lăng trụ tứ giác đều có cạnh đáy bằng a, chiều cao bằng 3a
Câu 3:
Tìm số các số nguyên dương a không vượt quá 10 để phương trình 91−1x2−a.31−1x2+2=0 có hai nghiệm phân biệt.
Câu 4:
Trong không gian Oxyz, cho hai điểm A(9;6;2) và B(-3;4;6). Biết điểm M(a;b;0) thuộc mặt phẳng (Oxy) sao cho |→MA+→MB| nhỏ nhất. Tính a + b
Câu 5:
Biết F(x) là một nguyên hàm của hàm số f(x)=1x trên (0;+∞) sao cho F(1) = 2. Tính F(3)
Câu 6:
Biết đồ thị hàm số y=x3−3x+2 cắt đường thẳng y = 2 - 4x tại điểm M(a;b). Tính a + b
Câu 7:
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;2;-3). Gọi A, B, C lần lượt là hình chiếu vuông góc của M lên các mặt phẳng (Oxy), (Oyz), (Ozx). Tính giá trị biểu thức T=OA2+2OB2−4OC2.
Câu 8:
Cho hàm số f(x) và g(x) cùng liên tục trên R. Khẳng định nào đúng
Câu 9:
Một viên đá hình trụ đặc có bán kính đáy bằng 2cm, chiều cao bằng 4cm được đặt vừa khít vào trong một chiếc ly rỗng có phần chứa nước là một hình nón như hình vẽ. Biết rằng chiều cao của phần chứa nước của ly gấp đôi chiều cao viên đá, miệng ly bằng bề mặt viên đá. Tính thể tích nước (ml) cần đổ vào ly cho đầy, làm tròn đến 2 chữ số thập phân sau dấu phẩy, biết do lực đẩy Archimedes, khi đổ nước vào, có 8% thể tích viên đá nổi lên phía trên mặt nước.
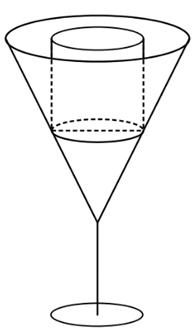
Một viên đá hình trụ đặc có bán kính đáy bằng 2cm, chiều cao bằng 4cm được đặt vừa khít vào trong một chiếc ly rỗng có phần chứa nước là một hình nón như hình vẽ. Biết rằng chiều cao của phần chứa nước của ly gấp đôi chiều cao viên đá, miệng ly bằng bề mặt viên đá. Tính thể tích nước (ml) cần đổ vào ly cho đầy, làm tròn đến 2 chữ số thập phân sau dấu phẩy, biết do lực đẩy Archimedes, khi đổ nước vào, có 8% thể tích viên đá nổi lên phía trên mặt nước.
Câu 10:
Cho hàm số f(x)=x3−3x2+2. Tìm tổng các số nguyên m sao cho phương trình f(x3−3x)=m có 7 nghiệm phân biệt.
Câu 11:
Một nguyên hàm của hàm số f(x)=x2+1x4+2x3−10x2−2x+1 có dạng F(x)=abln|x2−cx−1x2+dx−1|, trong đó a, b, c, d là các số nguyên dương và phân số ab tối giản. Tính a + b + c + d
Câu 12:
Cho hàm số y = f(x) có đạo hàm f' trên R. Hỏi có bao nhiêu giá trị nguyên thuộc [-10;10] của m để hàm số y = f(x) có 4 điểm cực trị?
Câu 14:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B và cạnh bên SA vuông góc với đáy. Gọi M là trung điểm của SC, biết AB = a, AC = 2a, SA = . Tính thể tích khối chóp S.AMB theo a
Câu 15:
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên dưới đây
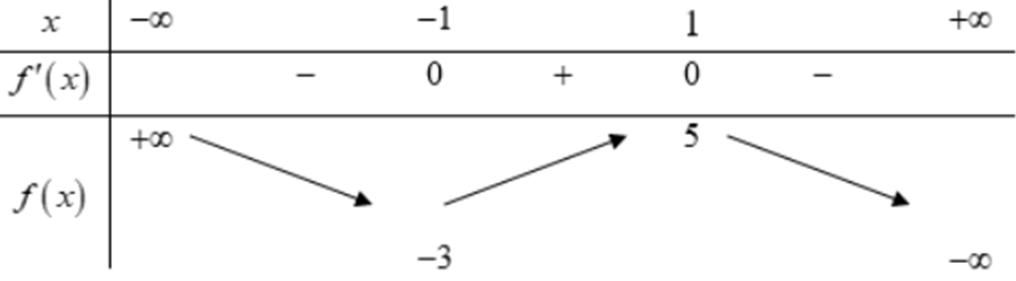Tìm tất cả các giá trị thực của tham số m để phương trình f(x) = m có ba nghiệm phân biệt?
Cho hàm số y = f(x) có đạo hàm trên R và có bảng biến thiên dưới đây
![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)