Câu hỏi:
13/07/2024 189
Cho ∆ABC biết \(\frac{{{{\cos }^2}A + {{\cos }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} = \frac{1}{2}\left( {{{\cot }^2}A + {{\cot }^2}B} \right)\). Khi đó ∆ABC là:
A. Tam giác cân;
B. Tam giác thường;
C. Tam giác đều;
D. Tam giác vuông.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: A
Ta có \(\frac{{{{\cos }^2}A + {{\cos }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} = \frac{1}{2}\left( {{{\cot }^2}A + {{\cot }^2}B} \right)\).
\( \Leftrightarrow \frac{{{{\cos }^2}A + {{\cos }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} + 1 = \frac{1}{2}\left( {1 + {{\cot }^2}A + 1 + {{\cot }^2}B} \right)\)
\( \Leftrightarrow \frac{{{{\cos }^2}A + {{\cos }^2}B + {{\sin }^2}A + {{\sin }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} = \frac{1}{2}\left( {\frac{1}{{{{\sin }^2}A}} + \frac{1}{{{{\sin }^2}B}}} \right)\)
\( \Leftrightarrow \frac{2}{{{{\sin }^2}A + {{\sin }^2}B}} = \frac{1}{2}.\frac{{{{\sin }^2}A + {{\sin }^2}B}}{{{{\sin }^2}A.{{\sin }^2}B}}\)
(Áp dụng kết quả Bài tập 5a và 5d, trang 65, Sách giáo khoa, Toán 10, Tập một).
⇔ (sin2A + sin2B)2 = 4.sin2A.sin2B
⇔ sin4A + 2.sin2A.sin2B + sin4B – 4.sin2A.sin2B = 0
⇔ sin4A – 2.sin2A.sin2B + sin4B = 0
⇔ (sin2A – sin2B)2 = 0
⇔ sin2A = sin2B
Theo hệ quả định lí sin, ta được \({\left( {\frac{a}{{2R}}} \right)^2} = {\left( {\frac{b}{{2R}}} \right)^2}\)
\( \Leftrightarrow \frac{{{a^2}}}{{{{\left( {2R} \right)}^2}}} = \frac{{{b^2}}}{{{{\left( {2R} \right)}^2}}}\)
⇔ a2 = b2
⇔ a = b hay BC = AC.
Vậy ∆ABC cân tại C.
Do đó ta chọn phương án A.
Hướng dẫn giải
Đáp án đúng là: A
Ta có \(\frac{{{{\cos }^2}A + {{\cos }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} = \frac{1}{2}\left( {{{\cot }^2}A + {{\cot }^2}B} \right)\).
\( \Leftrightarrow \frac{{{{\cos }^2}A + {{\cos }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} + 1 = \frac{1}{2}\left( {1 + {{\cot }^2}A + 1 + {{\cot }^2}B} \right)\)
\( \Leftrightarrow \frac{{{{\cos }^2}A + {{\cos }^2}B + {{\sin }^2}A + {{\sin }^2}B}}{{{{\sin }^2}A + {{\sin }^2}B}} = \frac{1}{2}\left( {\frac{1}{{{{\sin }^2}A}} + \frac{1}{{{{\sin }^2}B}}} \right)\)
\( \Leftrightarrow \frac{2}{{{{\sin }^2}A + {{\sin }^2}B}} = \frac{1}{2}.\frac{{{{\sin }^2}A + {{\sin }^2}B}}{{{{\sin }^2}A.{{\sin }^2}B}}\)
(Áp dụng kết quả Bài tập 5a và 5d, trang 65, Sách giáo khoa, Toán 10, Tập một).
⇔ (sin2A + sin2B)2 = 4.sin2A.sin2B
⇔ sin4A + 2.sin2A.sin2B + sin4B – 4.sin2A.sin2B = 0
⇔ sin4A – 2.sin2A.sin2B + sin4B = 0
⇔ (sin2A – sin2B)2 = 0
⇔ sin2A = sin2B
Theo hệ quả định lí sin, ta được \({\left( {\frac{a}{{2R}}} \right)^2} = {\left( {\frac{b}{{2R}}} \right)^2}\)
\( \Leftrightarrow \frac{{{a^2}}}{{{{\left( {2R} \right)}^2}}} = \frac{{{b^2}}}{{{{\left( {2R} \right)}^2}}}\)
⇔ a2 = b2
⇔ a = b hay BC = AC.
Vậy ∆ABC cân tại C.
Do đó ta chọn phương án A.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Khi khai quật một ngôi mộ cổ, người ta tìm được một mảnh của một chiếc đĩa phẳng hình tròn bị vỡ.
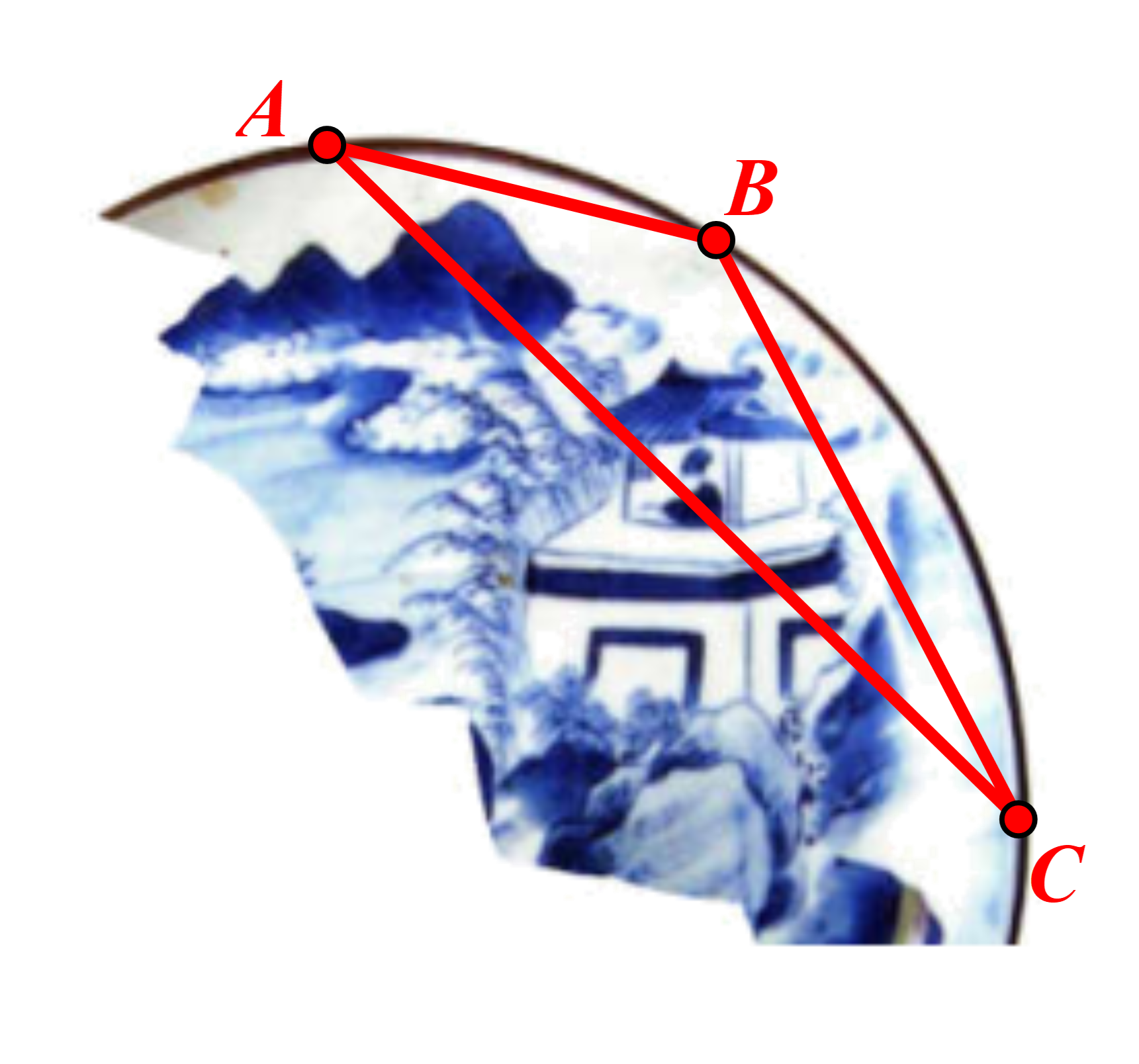
Họ muốn làm một chiếc đĩa mới phỏng theo chiếc đĩa này bằng cách tìm ra bán kính của chiếc đĩa. Khi lấy ba điểm A, B, C bất kì trên cung tròn (mép đĩa) thì họ đo được AB = 2,56 cm; BC = 4,18 cm và AC = 6,17 cm. Khi đó bán kính của chiếc đĩa bằng khoảng:
Câu 2:
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C.
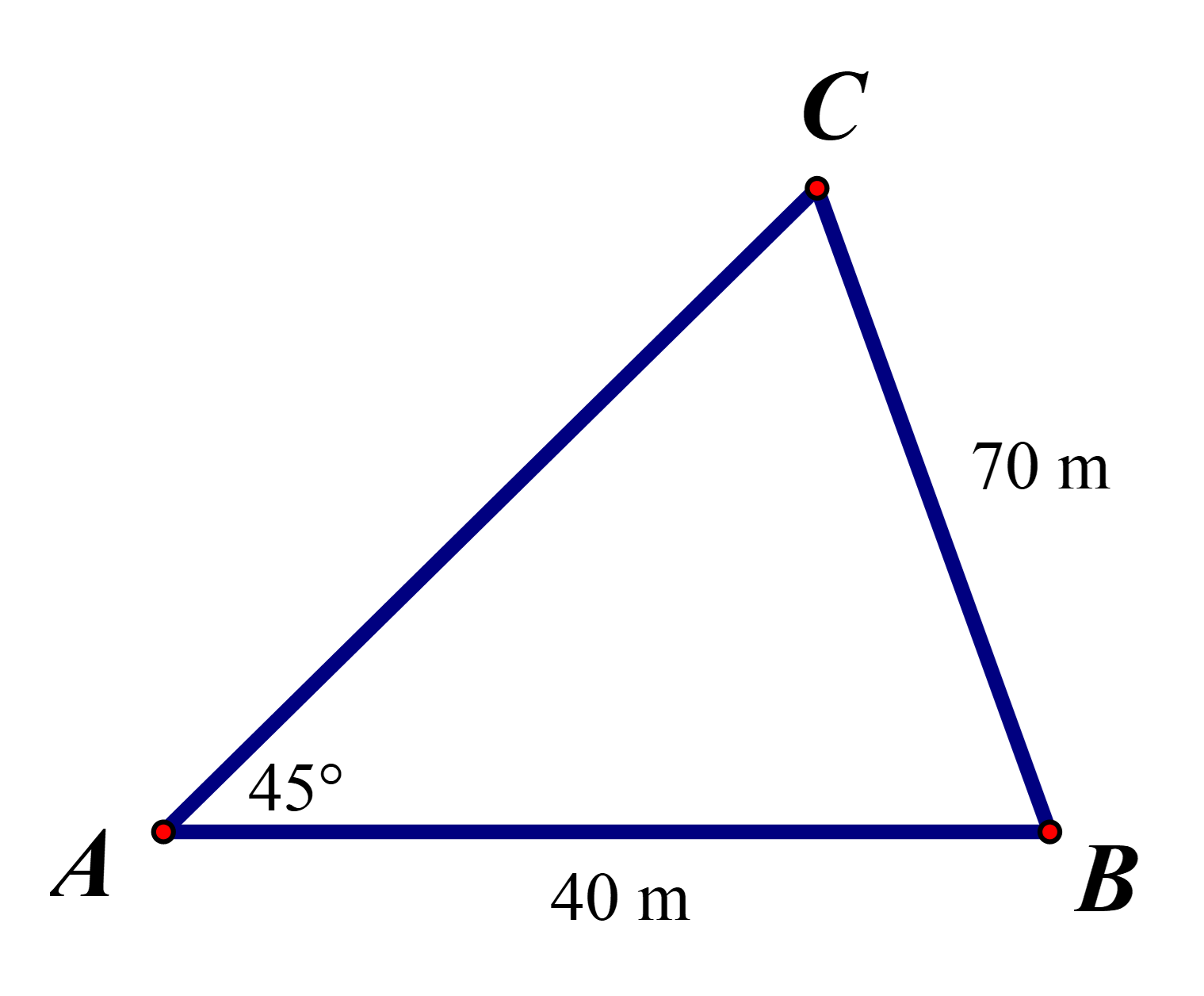
Người ta đo được khoảng cách AB = 40 m, BC = 70 m, \(\widehat {CAB} = 45^\circ \). Vậy sau khi đo đạc và tính toán, ta được khoảng cách AC gần nhất với giá trị nào sau đây?
Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C.

Người ta đo được khoảng cách AB = 40 m, BC = 70 m, \(\widehat {CAB} = 45^\circ \). Vậy sau khi đo đạc và tính toán, ta được khoảng cách AC gần nhất với giá trị nào sau đây?
Câu 3:
Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ.
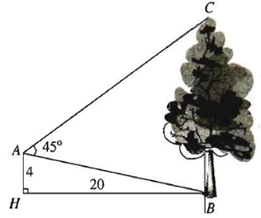
Biết vị trí quan sát cách mặt đất một khoảng AH = 4 m và khoảng cách từ chân đường vuông góc của vị trí quan sát A trên mặt đất tới gốc cây là HB = 20 m, \(\widehat {BAC} = 45^\circ \). Chiều cao của cây gần nhất với giá trị nào sau đây?
Từ vị trí A, người ta quan sát một cái cây cao mọc vuông góc với mặt đất như hình vẽ.

Biết vị trí quan sát cách mặt đất một khoảng AH = 4 m và khoảng cách từ chân đường vuông góc của vị trí quan sát A trên mặt đất tới gốc cây là HB = 20 m, \(\widehat {BAC} = 45^\circ \). Chiều cao của cây gần nhất với giá trị nào sau đây?
Câu 4:
Trên nóc một tòa nhà có một cột ăng-ten cao 5 m. Từ vị trí quan sát A cao 7 m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 50° và 40° so với phương nằm ngang.
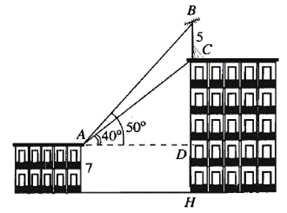
Chiều cao của tòa nhà gần nhất với giá trị nào sau đây?
Câu 5:
Cho ∆ABC thỏa mãn \[\sin A = \frac{{\sin B + \sin C}}{{\cos B + \cos C}}\]. Khi đó ∆ABC là:
Câu 6:
Cho ∆ABC có a.sinA + b.sinB + c.sinC = ha + hb + hc. Khi đó ∆ABC là:
Câu 7:
Từ hai vị trí A và B của một tòa nhà, người ta quan sát được đỉnh C của ngọn núi. Biết rằng độ cao của tòa nhà là AB = 70 m, phương nhìn AC tạo với phương ngang AH một góc bằng 30°, phương nhìn BC tạo với phương ngang BD một góc bằng 15°30’.
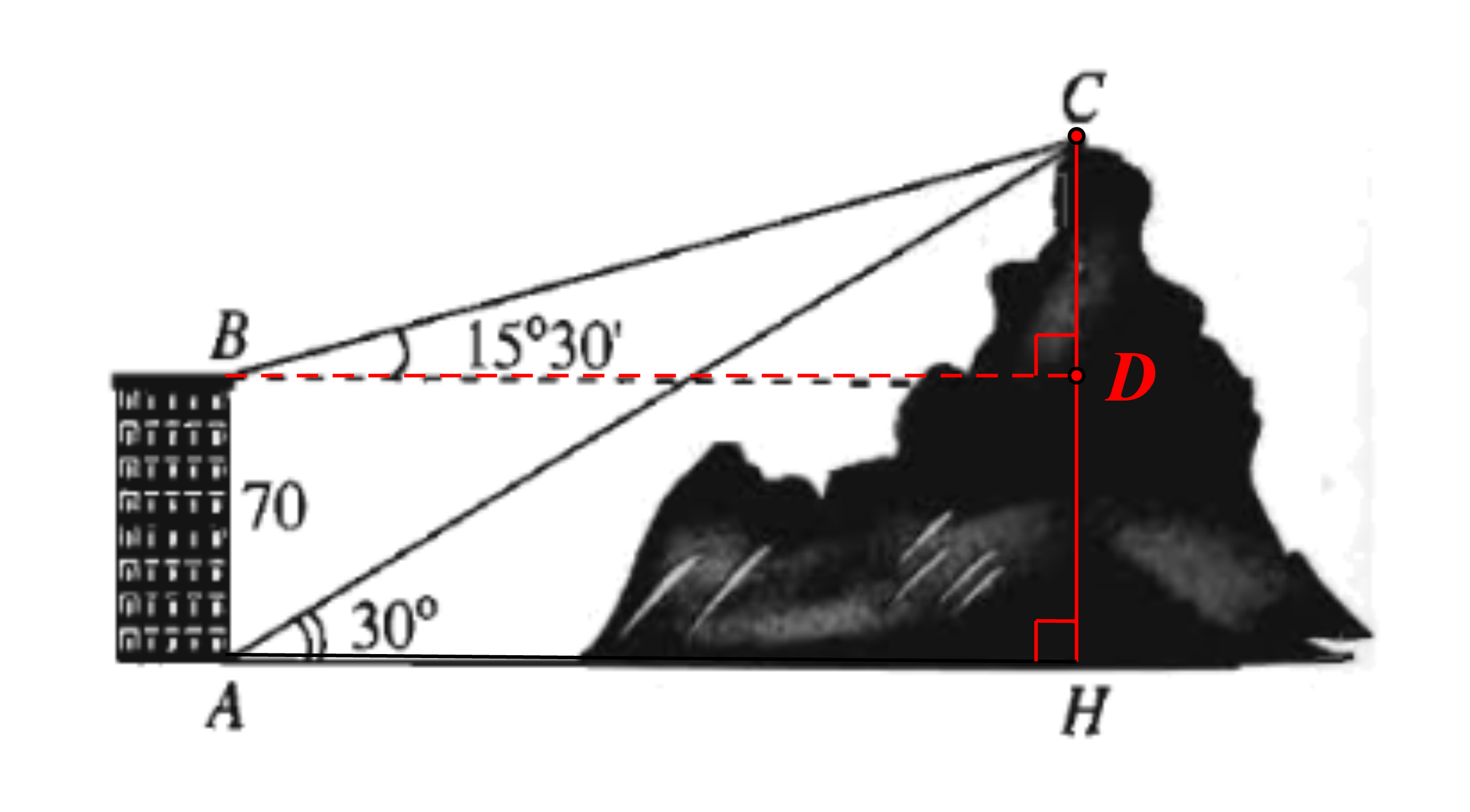
Ngọn núi đó có độ cao so với mặt đất gần nhất với giá trị nào sau đây?
Câu 8:
Cho ∆ABC thỏa mãn sin2A = sinB.sinC. Khẳng định nào sau đây đúng nhất?
Câu 9:
Giả sử CD = h là chiều cao của tháp, trong đó C là chân tháp.
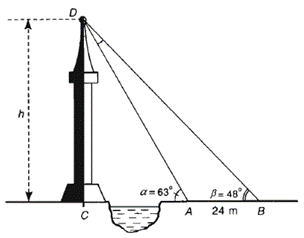
Một người đứng tại vị trí A (\(\widehat {CAD} = 63^\circ ),\) không sang được bờ bên kia để đo chiều cao h của tháp nên chọn thêm một điểm B (ba điểm A, B, C thẳng hàng) cách A một khoảng 24 m và \[\widehat {CBD} = 48^\circ \] để tính toán được chiều cao của tháp. Chiều cao h của tháp gần nhất với:


