Câu hỏi:
26/11/2024 260Các khoảng nghịch biến của hàm số là
A. (-∞;+∞)\{1}
B. (-∞;1)
C. (-∞;1) và (1;+∞)
D. (1;+∞)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án dúng là C
Lời giải
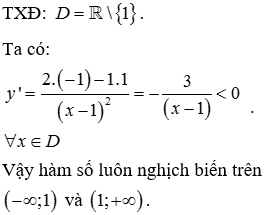
*Phương pháp giải:
1.Tìm tập xác định
2.Tính đạo hàm
3.Xét sự biên thiên
*Lý thuyết:
- Định nghĩa:
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K. Ta nói:
Hàm số y = f(x) đồng biến (tăng) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) nhỏ hơn f(x2), tức là
x1 < x2 f(x1) < f(x2).
Hàm số y = f(x) nghịch biến (giảm) trên K nếu với mọi cặp x1; x2 thuộc K mà x1 nhỏ hơn x2 thì f(x1) lớn hơn f(x2), tức là
x1 < x2 f(x1) > f(x2).
- Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là hàm số đơn điệu trên K.
- Nhận xét: Từ định nghĩa trên ta thấy:
a) f(x) đồng biến trên K
f(x) nghịch biến trên K
b) Nếu hàm số đồng biến trên K thì đồ thị đi lên từ trái sang phải.
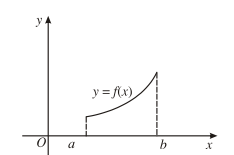
Nếu hàm số nghịch biến trên K thì đồ thị đi xuống từ trái sang phải.
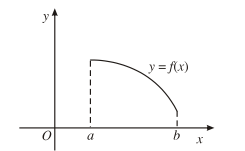
2. Tính đơn điệu và dấu của đạo hàm
- Định lí:
Cho hàm số y = f(x) có đạo hàm trên K.
a) Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K.
b) Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.
- Chú ý:
Nếu f’(x) = 0 với thì f(x) không đổi trên K.
Xem thêm
Lý thuyết Sự đồng biến, nghịch biến của hàm số (mới 2024 + Bài Tập) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có đáy ABC là tam giác vuông tại A và AB=AC=a. Biết góc giữa hai đường thẳng AC’ và BA’ bằng . Thể tích của khối lăng trụ ABC.A’B’C’ bằng
Câu 2:
Cho tam giác đều ABC có cạnh bằng 3a. Điểm H thuộc cạnh AC với HC=a. Dựng đoạn thẳng SH vuông góc với mặt phẳng (ABC) với SH=2a. Khoảng cách từ điểm C đến mặt phẳng (SAB) bằng
Câu 3:
Hình vẽ bên là đồ thị của hàm số y=f(x). Gọi S là tập hợp các giá trị nguyên không âm của tham số m để hàm số y=|f(x-2019)+m-2| có 5 điểm cực trị. Số các phần tử của S bằng
Câu 4:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, . Tính thể tích V của khối chóp S.ABCD
Câu 7:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S có SA=SB=2a nằm trong mặt phẳng vuông góc với đáy ABCD. Gọi α là góc giữa SD và mặt phẳng đáy (ABCD). Mệnh đề nào sau đây đúng
Câu 8:
Cho hình chóp đều S.ABC có đáy là tam giác đều cạnh a. Gọi M, N lần lượt là trung điểm của SB, SC. Biết . Thể tích của khối chóp S.ABC bằng
Câu 9:
Cho hàm số (với m là tham số thực) có bảng biến thiên dưới đây
Mệnh đề nào dưới đây đúng
Câu 10:
Cho hàm số f(x) > 0 với xÎR, f(0)=1 và với mọi xÎR. Mệnh đề nào dưới đây đúng
Câu 11:
Tìm các giá trị thực của tham số m để hàm số đồng biến trên khoảng (0;2)
Câu 12:
Cho hàm số y=f(x) có đạo hàm f’(x) trên R. Hình vẽ bên là đồ thị của hàm số y=f’(x). Hàm số nghịch biến trên khoảng nào trong các khoảng dưới đây
Câu 13:
Cho hàm số y=f(x) có đạo hàm . Tìm khoảng nghịch biến của đồ thị hàm số y=f(x)
Câu 15:
Xác định số thực x để dãy số theo thứ tự đó lập thành một cấp số cộng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)