Nội dung bài viết

    Xem thêm

    TOP 12 câu Trắc nghiệm Công thức lượng giác (Kết nối tri thức 2024) có đáp án - Toán 11

    Bộ 12 câu hỏi trắc nghiệm Toán lớp 11 Bài 2: Công thức lượng giác có đáp án đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 11 Bài 2.

    1 452 02/01/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Trắc nghiệm Toán 11 Bài 2: Công thức lượng giác

    Câu 1. Cho 0<α,β<π2 và thỏa mãn tanα=17, tanβ=34. Góc α+β có giá trị bằng

    A. π3.   B. π4.   C. π6.   D. π2.

    Đáp án đúng là: B

    Ta có tanα+β=tanα+tanβ1−tanα.tanβ=17+341−17.34=1 suy ra a + b = π4.

    Câu 2. Nếu tan(a+b) = 7, tan(a-b) = 4 thì giá trị đúng của tan2a là

    A. −1127.   B. 1127.   C. −1327.    D. 1327

    Đáp án đúng là: A

    Ta có tan2a = tan[(a+b)+(a-b)] = tana+b+tana−b1+tana+b.tana−b=7+41−7.4=−1127.

    Câu 3. Rút gọn biểu thức M = tanx - tany.

    A. M = tan(x-y).   B. M = sinx+ycosx.cosy.

    C. M = sinx−ycosx.cosy.   D. M = tanx−tany1+tanx.tany.

    Đáp án đúng là: C

    Ta có M = tanx - tany = sinxcosx−sinycosy=sinxcosy−cosxsinycosxcosy

    =sinx−ycosxcosy.

    Câu 4. Giá trị của biểu thức P=sin5π18cosπ9−sinπ9cos5π18cosπ4cosπ12−sinπ4sinπ12 là

    A. 1.   B. 12   C. 22    D. 32

    Đáp án đúng là: A

    Áp dụng công thức 12 Bài tập Công thức lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11

    Khi đó sin5π18cosπ9−sinπ9cos5π18=sin5π18−π9=sinπ6=12.

    Và cosπ4cosπ12−sinπ4sinπ12=cosπ4+π12=cosπ3=12.

    Vậy P=12:12=1.

    Câu 5. Trong ∆ABC, nếu sinBsinC= 2cosA thì ∆ABC là tam giác có tính chất nào sau đây?

    A. Cân tại B.   B. Cân tại A.   C. Cân tại C.   D. Vuông tại B.

    Đáp án đúng là: A

    Ta có sinBsinC= 2cosA⇒sinB = 2sinC.cosA = sin(C+A)+sin(C-A)

    Mặt khác A+B+C = π⇒B = π-(A+C) ⇒sinB = sin(A+C).

    Do đó, ta được sin(C-A) = 0⇒A = C.

    Câu 6. Cho góc α thỏa mãn π2<α<π và sinα=45. Tính P = sin2(α+π).

    A. P = -2425.   B. P = 2425.   C. P = -1225   D. P =1225.

    Đáp án đúng là: A

    Ta có P = sin2(α+π) = sin(2α+2π) = sin2α = 2sinαcosα.

    Từ hệ thức sin2α+cos2α=1, suy ra cosα=±1−sin2α=±35.

    Do π2<α<π nên ta chọn cosα=−35 .

    Thay sinα=45 và cosα=−35 vào P , ta được P=2.45.−35=−2425 .

    Câu 7. Cho x, y là các góc nhọn và dương thỏa mãn cotx = 34., coty = 17. Tổng x+y bằng

    A. π4.   B. 3π4.   C. π3.   D. π.

    Đáp án đúng là: B

    Ta có cot(x+y) = cotx.coty−1cotx+coty=34.17−134+17=−1.

    Mặt khác 0<x,y<π2 suy ra 0<x+y<π. Do đó x+y = 3π4.

    Câu 8. Nếu tanα và tanβ là hai nghiệm của phương trình x2+px+q = 0 (q≠1) thì tan(α+β) bằng

    A. pq−1.   B. -pq−1.   C. 2p1−q.   D. −2p1−q.

    Đáp án đúng là: A

    Vì tanα , tanβ là hai nghiệm của phương trình x2+px+q = 0 nên theo định lí Viet, ta có Khi đó

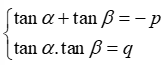
    12 Bài tập Công thức lượng giác (có đáp án) | Kết nối tri thức Trắc nghiệm Toán 11. Khi đó tan(α+β) = tanα+tanβ1−tanαtanβ=pq−1.

    Câu 9. Nếu α+β+γ = π2 và cotα + cotγ = 2cotβ thì cotα.cotγ bằng

    A. 3.   B. - 3 .   C. 3.   D. -3.

    Đáp án đúng là: C

    Từ giả thiết, ta có α+β+γ=π2⇒β=π2−α+γ.

    Suy ra cotα+cotγ=2cotβ=2.cotπ2−α+γ

    =2.tanα+γ=2.tanα+tanγ1−tanα.tanγ

    Mặt khác tanα+tanγ1−tanα.tanγ=1cotα+1cotγ1−1cotα.1cotγ=cotα+cotγcotα.cotγ−1 nên suy ra

    cotα+cotγ=2.cotα+cotγcotα.cotγ−1⇔cotα.cotγ−1=2⇔cotα.cotγ=3.

    Câu 10. Khẳng định nào sau đây đúng?

    A. sin(2018a) = 2018sina.cosa.

    B. sin(2018a) = 2018sin(1009a).cos(1009a).

    C. sin(2018a) = 2sinacosa.

    D. sin(2018a) = 2sin(1009a).cos(1009a).

    Đáp án đúng là: D

    Áp dụng công thức sin2α = 2sinα.cosα ta được

    sin(2018a) = 2sin(1009a).cos(1009a).

    Câu 11. Khẳng định nào sai trong các khẳng định sau?

    A. sin2x=1−cos2x2.   B. cos2x=1+cos2x2.

    C. sinx=2sinx2cosx2.   D. cos3x=cos3x−sin3x.

    Đáp án đúng là: D

    Ta có cos3x = 4cos3x - 3cosx.

    Câu 12. Công thức nào sau đây đúng?

    A. cos3a = 3cosa - 4cos3a.   B. cos3a = 4cos3a - 3cosa.

    C. cos3a = 3cos3a - 4cosa.   D. cos3a = 4cosa - 3cos3a.

    Đáp án đúng là: B

    Xem thêm

    Trắc nghiệm Toán 11 Bài 3: Hàm số lượng giác

    Trắc nghiệm Toán 11 Bài 4: Phương trình lượng giác cơ bản

    Trắc nghiệm Toán 11 Chương 1

    Trắc nghiệm Toán 11 Bài 1: Giá trị lượng giác của góc lượng giác

    Tham khảo các loạt bài Trắc nghiệm lớp 11 - Kết nối tri thức khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 452 02/01/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: