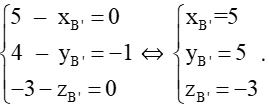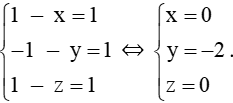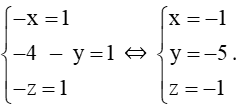Sách bài tập Toán 12 (Cánh diều): Bài tập cuối chương 2

Giải SBT Toán 12 Bài tập cuối chương 2 - Cánh diều

Bài 28 trang 76 SBT Toán 12 Tập 1: Cho điểm M thỏa mãn $\overrightarrow{OM}=\overrightarrow{i}-4\overrightarrow{j}+2\overrightarrow{k}$. Tọa độ của điểm M là:

A. (2; −4; 1).

B. (1; −4; 2).

C. (−4; 2; 1).

D. (−1; 4; −2).

Lời giải:

Đáp án đúng là: B

Ta có: $\overrightarrow{OM}=\overrightarrow{i}-4\overrightarrow{j}+2\overrightarrow{k}$ ⇒ $\overrightarrow{OM}$ = (1; −4; 2).

Vậy M(1; −4; 2).

Bài 29 trang 76 SBT Toán 12 Tập 1: Cho hai điểm M(3; −2; 3) và N(1; −4; 5). Tọa độ của vectơ $\overrightarrow{MN}$ là:

A. (−2; −2; 2).

B. (2; 2; −2).

C. (−2; −6; 2).

D. (2; −6; −2).

Lời giải:

Đáp án đúng là: A

Ta có: $\overrightarrow{MN}$ = (1 – 3; −4 – (−2); 5 – 3) = (−2; −2; 2).

Vậy $\overrightarrow{MN}$ = (−2; −2; 2).

Bài 30 trang 76 SBT Toán 12 Tập 1: Cho hai vectơ $\overrightarrow{u}$ = (3; 4; −5), $\overrightarrow{v}$ = (5; −7; 1). Tọa độ của vectơ $\overrightarrow{u}+\overrightarrow{v}$ là:

A. (8; 11; −4).

B. (−2; 11; −6).

C. (8; −3; −4).

D. (−8; 3; 4).

Lời giải:

Đáp án đúng là: C

Ta có: $\overrightarrow{u}+\overrightarrow{v}$ = (3 + 5; 4 + (−7); −5 + 1) = (8; −3; −4).

Vậy $\overrightarrow{u}+\overrightarrow{v}$ = (8; −3; −4).

Bài 31 trang 76 SBT Toán 12 Tập 1: Cho hai vectơ $\overrightarrow{u}$ = (2; −2; 1), $\overrightarrow{v}$ = (5; −4; −1). Tọa độ của vectơ $\overrightarrow{u}-\overrightarrow{v}$ là:

A. (−3; 2; 2).

B. (7; −6; 0).

C. (3; −2; −2).

D. (−3; −6; 0).

Lời giải:

Đáp án đúng là: A

Ta có: $\overrightarrow{u}-\overrightarrow{v}$ = (2 – 5; −2 – (−4); 1 – (−1)) = (−3; 2; 2).

Vậy $\overrightarrow{u}-\overrightarrow{v}$ = (−3; 2; 2).

Bài 32 trang 76 SBT Toán 12 Tập 1: Cho vectơ $\overrightarrow{u}$ = (1; 2; −3). Tọa độ của vectơ −3$\overrightarrow{u}$ là:

A. (3; 6; −9).

B. (−3; −6; −9).

C. (3; 6; 9).

D. (−3; −6; 9).

Lời giải:

Đáp án đúng là: D

Ta có: $\overrightarrow{u}$ = (1; 2; −3) ⇒ −3$\overrightarrow{u}$ = (−3.1; −3.2; −3.(−3)) = (−3; −6; 9).

Vậy −3$\overrightarrow{u}$ = (−3; −6; 9).

Bài 33 trang 76 SBT Toán 12 Tập 1: Độ dài của vectơ $\overrightarrow{u}$ = (1; 2; 2) là:

A. 9

B. 3.

C. 5.

D. 4.

Lời giải:

Đáp án đúng là: B

Ta có: $\overrightarrow{u}$ = (1; 2; 2) ⇒ |$\overrightarrow{u}$| = $\sqrt{1^2+2^2+2^2}$ = 3.

Vậy độ dài vectơ $\overrightarrow{u}$ là 3.

Bài 34 trang 76 SBT Toán 12 Tập 1: Tích vô hướng của hai vectơ $\overrightarrow{u}$ = (−2; 1; 3) và $\overrightarrow{v}$ = (−3; 2; 5) là:

A. $\sqrt{14}.\sqrt{38}$.

B. $-\sqrt{14}.\sqrt{38}$.

C. 23.

D. −23.

Lời giải:

Đáp án đúng là: C

Ta có: $\overrightarrow{u}$.$\overrightarrow{v}$ = (−2).(−3) + 1.2 + 3.5 = 23.

Vậy tích vô hướng của hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ là 23.

Bài 35 trang 76 SBT Toán 12 Tập 1: Khoảng cách giữa hai điểm I(2; −3; −4) và K(7; −3; 8) là:

A. 169.

B. 13.

C. 26.

D. 17.

Lời giải:

Đáp án đúng là: B

Ta có: $\overrightarrow{IK}$ = (5; 0; 12).

IK = |$\overrightarrow{IK}$| = $\sqrt{5^2+0^2+{12}^2}$ = 13.

Vậy khoảng cách giữa hai điểm I và K là 13.

Bài 36 trang 76 SBT Toán 12 Tập 1: Cho hai điểm M(5; 2; −3) và N(1; −4; 5). Trung điểm của đoạn thẳng MN có tọa độ là:

A. (4; 6; −8).

B. (2; 3; −4).

C. (6; −2; 2).

D. (3; −1; 1).

Lời giải:

Đáp án đúng là: D

Gọi I(x; y; z) là trung điểm đoạn thẳng MN, ta có:

x = $\frac{x_M+x_N}{2}$ = $\frac{5+1}{2}$ = 3.

y = $\frac{y_M+y_N}{2}$ = $\frac{2+(-4)}{2}$ = −1.

z = $\frac{z_M+z_N}{2}$ = $\frac{-3+5}{2}$ = 1.

Vậy trung điểm của đoạn thẳng MN có tọa độ (3; −1; 1).

Bài 37 trang 77 SBT Toán 12 Tập 1: Cho tam giác MNP có M(1; −2; 1), N(−1; −2; 3) và P(3; 1; 2). Trọng tâm của tam giác MNP có tọa độ là:

A. (1; −1; 2).

B. (3; −3; 6).

C. (−1; 1; −2).

D. (−3; 3; −6).

Lời giải:

Đáp án đúng là: A

Gọi G(x; y; z) là trọng tâm tam giác MNP, lúc này ta có:

x = $\frac{x_M+x_N+x_P}{3}$ = $\frac{1+(-1)+3}{3}$ = 1;

y = $\frac{y_M+y_N+y_P}{3}$ = $\frac{-2+(-2)+1}{3}$ = −1;

z = $\frac{z_M+z_N+z_P}{3}$ = $\frac{1+3+2}{3}$ = 2.

Vậy trọng tâm tam giác MNP có tọa độ (1; −1; 2).

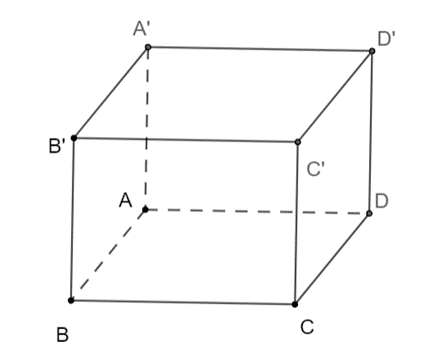
Bài 38 trang 77 SBT Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' có A(2; −1; 3), B(3; 0; 4), D(2; −2; 3), C'(5; 4; −3).

Lời giải:

Ta có: $\overrightarrow{AD}$ = (2 – 2; −2 – (−1); 3 – 3) = (0; −1; 0).

Gọi tọa độ của B' là (x _B'; y _B'; z _B'), ta có tọa độ của vectơ $\overrightarrow{B\text{'}C\text{'}}$ là:

$\overrightarrow{B\text{'}C\text{'}}$ = (5 – x _B'; 4 – y _B'; −3 − z _B').

Trong hình hộp ABCD.A'B'C'D', ta có:

$\overrightarrow{B\text{'}C\text{'}}$ = $\overrightarrow{AD}$ (do hai vectơ cùng hướng và có AD = B'C').

Ta có: $\overrightarrow{B\text{'}C\text{'}}$ = $\overrightarrow{AD}$ ⇔

Vậy tọa độ điểm B' là (5; 5; −3).

Bài 39 trang 77 SBT Toán 12 Tập 1: Trong không gian với hệ trục Oxyz, cho A(1; 0; 1), B(2; 1; 2), C(1; −1; 1).

Lời giải:

Ta có: $\overrightarrow{AB}$ = (1; 1; 1); $\overrightarrow{AC}$ = (0; −1; 0).

Nhận thấy $\overrightarrow{AB}$ ≠ k$\overrightarrow{AC}$ với mọi k ∈ ℝ.

Vậy A, B, C không thẳng hàng.

Gọi D(x; y; z) thỏa mãn $\overrightarrow{AB}=\overrightarrow{DC}$, ta có: $\overrightarrow{DC}$ = (1 – x; −1 – y; 1 – z);

Vì tọa độ điểm D thỏa mãn $\overrightarrow{AB}=\overrightarrow{DC}$ nên

Do đó, tọa độ điểm D(0; −2; 0).

Ta có: $\overrightarrow{BC}$ = (−1; −2; −1) nên BC = |$\overrightarrow{BC}$| = $\sqrt{{(-1)}^2+{(-2)}^2+{(-1)}^2}$ = $\sqrt{6}$.

Ta có: cos$\widehat{BAC}$ = cos($\overrightarrow{AB}$, $\overrightarrow{AC}$) = $\frac{1.0+1.(-1)+1.0}{\sqrt{1^2+1^2+1^2}.\sqrt{0^2+{(-1)}^2+0^2}}$ = $\frac{-1}{\sqrt{3}}$.

Bài 40 trang 77 SBT Toán 12 Tập 1: Cho hai vectơ $\overrightarrow{u}$ = (2; −2; −3) và $\overrightarrow{v}$ = (3; 3; 5). Hãy chỉ ra tọa độ của một vectơ $\overrightarrow{w}$ vuông góc với cả hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$

Lời giải:

Ta có: 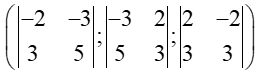$\overrightarrow{w}$ = [$\overrightarrow{u}$,$\overrightarrow{v}$] = = (−1; −19; 12).

Khi đó, vectơ $\overrightarrow{w}$ = (−1; −19; 12) cùng vuông góc với cả hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$

Bài 41 trang 77 SBT Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Tính:

a, $\overrightarrow{A\text{'}B}.\overrightarrow{B\text{'}C\text{'}}$;

b) $\overrightarrow{D\text{'}A}.\overrightarrow{BA\text{'}}$.

Lời giải:

a) Ta có: B'C' ⊥ (ABB'A') nên B'C'⊥ A'B. Vậy $\overrightarrow{A\text{'}B}.\overrightarrow{B\text{'}C\text{'}}$ = 0.

b)

Ta có: $\left(\overrightarrow{D\text{'}A},\overrightarrow{BA\text{'}}\right)$ = $\left(\overrightarrow{D\text{'}A},\overrightarrow{CD\text{'}}\right)$ = 180° − $\widehat{CD\text{'}A}$ = 120°.

Sử dụng định nghĩa tích vô hướng của hai vectơ trong không gian, ta có:

$\overrightarrow{D\text{'}A}.\overrightarrow{BA\text{'}}$ = |$\overrightarrow{D\text{'}A}$| . |$\overrightarrow{BA\text{'}}$| . cos$\left(\overrightarrow{D\text{'}A},\overrightarrow{BA\text{'}}\right)$

   = $a\sqrt{2}.a\sqrt{2}.\cos 120°$

   = −a².

Bài 42 trang 77 SBT Toán 12 Tập 1: Trong không gian với hệ tọa độ Oxyz, cho A(1; 0; 1), B(2; 1; 2) và C(0; −4; 0).

a) Chứng minh rằng ba điểm A, B, C không thẳng hàng.

b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

c) Tìm tọa độ trọng tâm G của tam giác ABC.

d) Tính chu vi tam giác ABC.

e) Tính cos$\widehat{BAC}$.

Lời giải:

a) Ta có: $\overrightarrow{AB}$ = (1; 1; 1); $\overrightarrow{AC}$ = (−1; −4; −1); k$\overrightarrow{AC}$ = (−k; −4k; −k).

Nhận thấy $\overrightarrow{AB}$ ≠ k$\overrightarrow{AC}$ với mọi k ∈ ℝ.

Vậy ba điểm A, B, C không thẳng hàng.

b) Gọi tọa độ điểm D là D(x; y; z). Ta có: $\overrightarrow{DC}$ = (−x; −4 – y; −z).

Tứ giác ABCD là hình bình hành khi và chỉ khi $\overrightarrow{AB}=\overrightarrow{DC}$ ⇔

Vậy D(−1; −5; −1).

c) Gọi G(x_G; y_G; z_G) là trọng tâm tam giác ABC, lúc này ta có:

x_G = $\frac{x_A+x_B+x_C}{3}$ = $\frac{1+2+0}{3}$ = 1;

y_G = $\frac{y_A+y_B+y_C}{3}$ = $\frac{0+1+(-4)}{3}$ = −1;

z_G = $\frac{z_A+z_B+z_C}{3}$ = $\frac{1+2+0}{3}$ = 1.

Vậy tọa độ của điểm G(1; −1; 1).

d) Ta có: AB = |$\overrightarrow{AB}$| = $\sqrt{1^2+1^2+1^2}$ = $\sqrt{3}$;

   AC = |$\overrightarrow{AC}$| = $\sqrt{{(-1)}^2+{(-4)}^2+{(-1)}^2}$ = 3$\sqrt{2}$;

   BC = |$\overrightarrow{BC}$| = $\sqrt{{(0-2)}^2+{(-4-1)}^2+{(0-2)}^2}$ = $\sqrt{33}$.

Vậy chu vi tam giác ABC là: $\sqrt{3}$ + 3$\sqrt{2}$ + $\sqrt{33}$.

e) Trong tam giác ABC, ta có:

cos$\widehat{BAC}$ = $\cos \left(\overrightarrow{AB},\overrightarrow{AC}\right)$ = = $\frac{1.(-1)+1.(-4)+1.(-1)}{\sqrt{3}.3\sqrt{2}}$ = $\frac{-\sqrt{6}}{3}.$

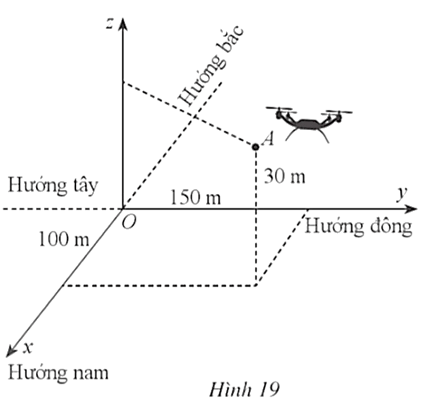
Bài 43 trang 78 SBT Toán 12 Tập 1: Một người điều khiển một flycam để phục vụ trong một chương trình của đài truyền hình. Đầu tiên flycam ở vị trí A cách vị trí điều khiển 100 m về phía nam và 150 m về phía đông, đồng thời cách mặt đất 30 m (Hình 19). Để thực hiện nhiệm vụ tiếp theo, người điều khiển flycam đến vị trí B cách vị trí điều khiển 80 m về phía bắc và 120 m về phía tây, đồng thời cách mặt đất 50 m.

Chọn hệ trục tọa độ Oxyz với gốc O là vị trí người điều khiển, mặt phẳng (Oxy) trùng với mặt đất, trục Ox có hướng trùng với hướng nam, trục Oy có hướng trùng với hướng đông, trục Oz vuông góc với mặt đất hướng lên bầu trời, mỗi đơn vị trên các trục tương ứng với 1 m.

a) Xác định tọa độ của flycam tại mỗi vị trí A, B đối với hệ tọa độ đã chọn.

b) Tính quãng đường flycam bay từ vị trí A đến vị trí B, biết flycam bay từ vị trí A đến vị trí B theo một đường thẳng (làm tròn kết quả đến hàng đơn vị của mét).

Lời giải:

a) Theo giả thiết đề cho, ta có:

Tọa độ của flycam tại vị trí điểm A là (100; 150; 30).

Tọa độ của flycam tại vị trí điểm B là (−80; −120; 50).

b) Quãng đường flycam bay từ vị trí A đến vị trí B bằng khoảng cách giữa hai điểm A và B, ta có:

AB = $\sqrt{{(-80-100)}^2+{(-120-150)}^2+{(50-30)}^2}$ = $\sqrt{105700}$ ≈ 325 (m).

Xem thêm Lời giải bài tập Toán 12 sách Cánh diều hay, chi tiết khác:

Bài 1: Khoảng biến thiên, khoảng tứ phân vị của mẫu số liệu ghép nhóm

Bài 2: Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm

Bài tập cuối chương 3

Bài 1: Nguyên hàm

Bài 2: Nguyên hàm của một số hàm số sơ cấp