Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 12 Bài 4 (Cánh diều): Ứng dụng hình học của tích phân

    Với giải sách bài tập Toán 12 Bài 4: Ứng dụng hình học của tích phân sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 12 Bài 4.

    1 191 15/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 12 Bài 4: Ứng dụng hình học của tích phân - Cánh diều

    Bài 45 trang 26 SBT Toán 12 Tập 2: Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = x3, y = x2 và hai đường thẳng x = 1, x = 3 là:

    A. ∫13(x3−x2)dx

    B. ∫13(x2−x3)dx

    C. ∫13x2dx−∫13x3dx

    D. ∫13x2dx+∫13x3dx

    Lời giải:

    Đáp án đúng là: A

    Diện tích hình phẳng đã cho là: S = ∫13|x3−x2|dx=∫13(x3−x2)dx

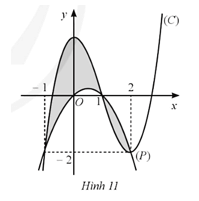
    Bài 46 trang 26 SBT Toán 12 Tập 2: Cho các hàm số y = f(x), y = g(x) có đồ thị hàm số lần lượt là (P), (C) và hình phẳng được tô màu như Hình 11. Công thức tính diện tích hình phẳng được tô màu là:

    Cho các hàm số y = f(x), y = g(x) có đồ thị hàm số lần lượt là (P), (C) và hình phẳng được tô màu như Hình 11

    A. S = ∫−11[g(x)−f(x)]dx+∫12[g(x)−f(x)]dx.

    B. S = ∫−11[g(x)−f(x)]dx−∫12[g(x)−f(x)]dx.

    C. S = ∫−12[g(x)−f(x)]dx.

    D. S = ∫−12[g(x)−f(x)]dx.

    Lời giải:

    Đáp án đúng là: B

    Dựa vào đồ thị, ta có, công thức tính diện tích hình phẳng được tô màu là:

    S = ∫−12f(x)−g(x)dx = ∫−11fx−gxdx+∫12fx−gxdx

    = ∫−11g(x)−f(x)dx+∫12fx−gxdx

    = ∫−11[g(x)−f(x)]dx+∫12−[g(x)−f(x)]dx

    = ∫−11[g(x)−f(x)]dx−∫12[g(x)−f(x)]dx.

    Bài 47 trang 26 SBT Toán 12 Tập 2: Cho hình phẳng giới hạn bởi đồ thị hàm số y = x, trục hoành và hai đường thẳng x = 0, x = 2 quay quanh trục Ox được khối tròn xoay có thể tích tính theo công thức:

    A. ∫02xdx

    B. π∫02x2dx

    C. ∫02x2dx

    D. π∫02xdx

    Lời giải:

    Đáp án đúng là: B

    Thể tích khối tròn xoay đã cho là: V = π∫02x2dx

    Bài 48 trang 27 SBT Toán 12 Tập 2: Trong mỗi ý a), b), c), d), chọn phương án: đúng (Đ) hoặc sai (S).

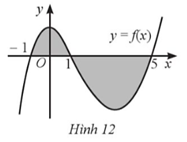
    Cho hình phẳng được tô màu như Hình 12. Diện tích hình phẳng được kí hiệu là S

    Cho hình phẳng được tô màu như Hình 12. Diện tích hình phẳng được kí hiệu là S

    a) Hình phẳng đó được giới hạn bởi đồ thị y = f(x), trục hoành và hai đường thẳng x = −1, x = 5.

    Đ

    S

    b) S = ∫−15|f(x)|dx.

    Đ

    S

    c) S = ∫−11f(x)dx+∫15f(x)dx

    Đ

    S

    d) S = ∫−11f(x)dx−∫15f(x)dx

    Đ

    S

    Lời giải:

    a) Đ

    b) Đ

    c) S

    d) Đ

    Quan sát đồ thị, ta có hình phẳng được tô màu như Hình 12 được giới hạn đồ thị y = f(x), trục hoành và hai đường thẳng x = −1, x = 5.

    Diện tích hình phẳng đó là:

    S = ∫−15|f(x)|dx =∫−11f(x)dx+∫15f(x)dx

    =∫−11f(x)dx+∫15−f(x)dx=∫−11f(x)dx−∫15f(x)dx.

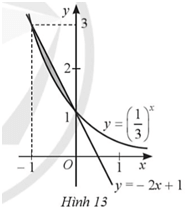
    Bài 49 trang 27 SBT Toán 12 Tập 2: Cho hình phẳng được tô màu như Hình 13.

    Cho hình phẳng được tô màu như Hình 13 trang 27 SBT Toán 12 Tập 2

    a) Hình phẳng đó được giới hạn bởi các đường nào?

    b) Tính diện tích hình phẳng đó.

    Lời giải:

    a) Quan sát đồ thị ta thấy, hình phẳng được tô màu như Hình 13 được giới hạn bởi đồ thị các hàm số y = 13x, y = −2x + 1 và hai đường thẳng x = −1, x = 0.

    b) Diện tích hình phẳng đó là:

    S = ∫−1013x−(−2x+1)dx=∫−10−2x+1−13xdx

    = −x2+x+13xln3−10 = 1ln3−−2+3ln3=2−2ln3.

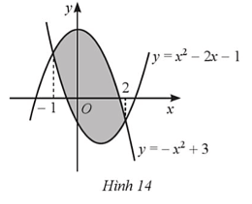
    Bài 50 trang 27 SBT Toán 12 Tập 2: Cho hình phẳng được tô màu như Hình 14.

    Cho hình phẳng được tô màu như Hình 14. Hình phẳng đó được giới hạn bởi các đường nào?

    a) Hình phẳng đó được giới hạn bởi các đường nào?

    b) Tính diện tích hình phẳng đó.

    Lời giải:

    a) Quan sát đồ thị ta thấy, hình phẳng được tô màu trong Hình 14 được hạn bởi đồ thị các hàm số y = −x2 + 3, y = x2 – 2x – 1 và hai đường thẳng x = −1, x = 2.

    b) Diện tích hình phẳng đó là:

    S = ∫−12(−x2+3)−(x2−2x−1)dx

    = ∫−12(−x2+3)−(x2−2x−1)dx

    = ∫−12(−2x2+2x+4)dx

    = −23x3+x2+4x−12

    = 9.

    Vậy diện tích hình phẳng đó bằng 9.

    Bài 51 trang 27 SBT Toán 12 Tập 2: Cho hình phẳng giới hạn bởi đồ thị hàm số y = cosx2, trục hoành và hai đường thẳng x = 0, x = π2. Tính thể tích khối tròn xoay tạo thành khi cho hình phẳng đó quay quanh trục Ox.

    Lời giải:

    Thể tích khối tròn xoay đã cho là:

    V = π∫0π2cos2x2dx=π∫0π21+cosx2dx=π(x+sinx)20π2=π2+2π4.

    Xem thêm Lời giải bài tập Toán 12 sách Cánh diều hay, chi tiết khác:

    Bài tập cuối chương 3

    Bài 1: Nguyên hàm

    Bài 2: Nguyên hàm của một số hàm số sơ cấp

    Bài 3: Tích phân

    Bài tập cuối chương 4

    Tham khảo các loạt bài Toán 12 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 191 15/08/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: