Trắc nghiệm Toán 10 Bài tập ôn tập chương 3 có đáp án
Trắc nghiệm Toán 10 Bài tập ôn tập chương 3 có đáp án
-
298 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Điểm nào sau đây thuộc đồ thị hàm số y = 4x + 1
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
- Thay x = 2; y = 3 vào hàm số ta được: 3 = 4.1 + 1 (vô lí). Do đó, (2; 3) không thuộc đồ thị hàm số.
- Thay x = 0; y = 1 vào hàm số ta được: 1 = 0.1 + 1 (luôn đúng). Do đó, (0; 1) thuộc đồ thị hàm số.
- Thay x = 4; y = 5 vào hàm số ta được: 5 = 4.4 + 1 (vô lí). Do đó, (4; 5) không thuộc đồ thị hàm số.
- Thay x = 0; y = 0 vào hàm số ta được: 0 = 4.0 + 1 (vô lí). Do đó, (0; 0) không thuộc đồ thị hàm số.
Câu 2:
23/07/2024Cho hàm số y = f(x) = . Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Thay lần lượt các giá trị: 3; (-1); (-2); 1 vào biểu thức .
Ta được: Khi x = 3 thay vào hàm số y: . (Chọn A)
Câu 3:
16/07/2024Tập xác định của hàm số y = là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hàm số y = xác định khi 2x - 2 ≠ 0
Như vậy tập xác định của hàm số là
D = \{1}
Câu 4:
22/07/2024Tập xác định của hàm số y = là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hàm số y = xác định
Như vậy tập xác định của hàm số là
D = .
Câu 5:
15/07/2024Tìm tập xác định của hàm số y = f(x) =
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Với x 1 thì f(x) = xác định với mọi x 1 (1)
Với x < 1 thì f(x) = . Khi đó hàm số xác định nếu x + 1 . Kết hợp với điều kiện x < 1 thì f(x) = xác định khi (2)
Kết hợp (1) và (2) ta được f(x) xác định với mọi x -1 hay D = [-1; )
Câu 6:
12/07/2024Tìm tập xác định của y =
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Để hàm số y xác định thì . Tập xác định: D = [1; 2]
Câu 7:
12/07/2024Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây? 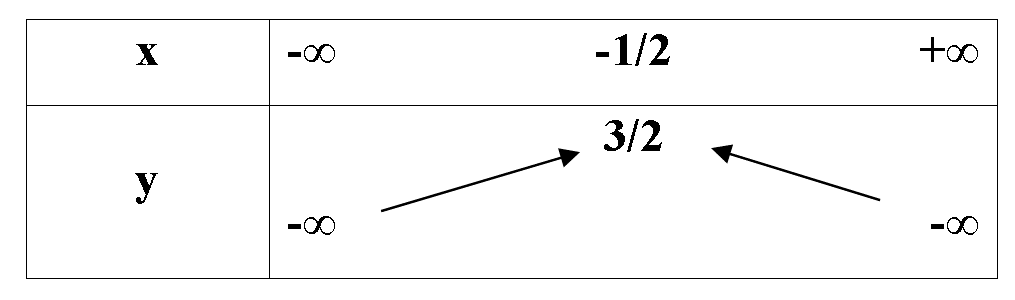
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Bảng biến thiên có bề lõm hướng xuống nên a < 0. Do đó, loại đáp án A và B.
Đỉnh của parabol có tọa độ là . Xét các đáp án còn lại:
- Thay x = ; y = vào phương trình :
.
(Vô lý). Như vậy điểm không thuộc đồ thị của hàm số.
- Thay x = ; y = vào phương trình :
. Như vậy thuộc đồ thị hàm số
Câu 8:
22/07/2024Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?

 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Parabol có bề lõm hướng lên nên a > 0. Loại đáp án A, B.
Parabol cắt trục hoành tại điểm , thay x = 1; y = 0 vào các phương trình:
- Thay x = 1; y = 0 vào :
0 = 2.- 3.1 + 1 = 0 như vậy điểm (1; 0) thuộc đồ thị hàm số.
- Thay x = 1; y = 0 vào :
0 = - 3.1 + 1 = -1 như vậy điểm (1; 0) không thuộc đồ thị hàm số
Câu 9:
23/07/2024Đồ thị sau đây là đồ thị của hàm số nào trong các phương án dưới đây?

 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Bề lõm quay xuống nên a < 0 nên loại C.
Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt nên loại A. Vì phương trình hoành độ giao điểm của hàm số với trục hoành ở đáp án A là vô nghiệm.
Xét phương trình hoành độ giao điểm của hàm số với trục hoành ở đáp án B, ta có
.
Quan sát đồ thị ta thấy đồ thị hàm số không cắt trục hoành tại điểm có hoành độ bằng ![]() Do đó đáp án B không phù hợp. Dùng phương pháp loại trừ, thì D là đáp án đúng.
Do đó đáp án B không phù hợp. Dùng phương pháp loại trừ, thì D là đáp án đúng.
Câu 10:
23/07/2024Cho hàm số có đồ thị như hình sau. Khẳng định nào sau đây đúng?

 Xem đáp án
Xem đáp án
Đáp án đúng là: B
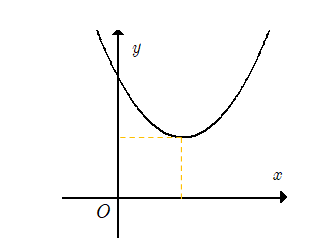
Bề lõm hướng lên nên
Hoành độ đỉnh parabol (vì a > 0) nên
Parabol cắt trục tung tại điểm có tung độ dương nên
Câu 11:
23/07/2024Cho hàm số có đồ thị như hình sau. Khẳng định nào sau đây đúng?
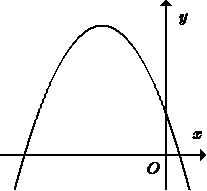
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
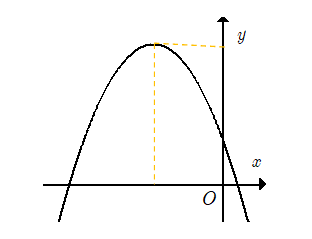
Bề lõm hướng xuống nên
Hoành độ đỉnh parabol (do a < 0) nên
Parabol cắt trục tung tại điểm có tung độ dương nên
Câu 12:
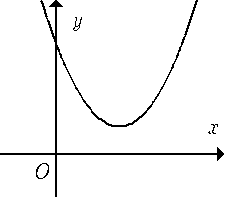
12/07/2024Cho parabol . Xét dấu hệ số a và biệt thức khi (P) hoàn toàn nằm phía trên trục hoành.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
(P) hoàn toàn nằm phía trên trục hoành khi bề lõm hướng lên và đỉnh có tung độ dương (hình vẽ).
Câu 14:
22/07/2024Tam thức bậc hai :
 Xem đáp án
Xem đáp án
Đáp án đúng là : C
Ta có .
Bảng xét dấu
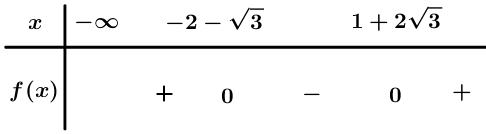
Dựa vào bảng xét dấu .
Câu 15:
22/07/2024Cho có . Khi đó mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì và nên không đổi dấu trên .
Câu 16:
12/07/2024Tam thức bậc hai nhận giá trị dương khi và chỉ khi
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có :
Câu 17:
12/07/2024Dấu của tam thức bậc hai: được xác định như sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là : C
Ta có : .
Bảng xét dấu
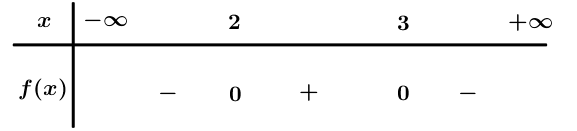
Dựa vào bảng xét dấu ta được
với và với x < 2 hoặc x > 3.
Câu 19:
19/07/2024Tập nghiệm của bất phương trình: là:
 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Ta có : f(x) = .
Bảng xét dấu
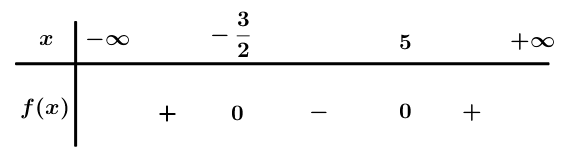
Dựa vào bảng xét dấu
Câu 20:
16/07/2024Tập nghiệm của bất phương trình là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có : .
Bảng xét dấu
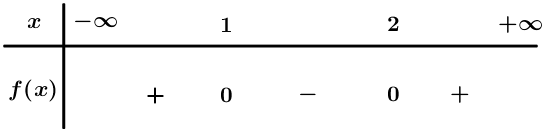
Dựa vào bảng xét dấu .
Câu 21:
22/07/2024Tập nghiệm của bất phương trình là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: .
Bảng xét dấu
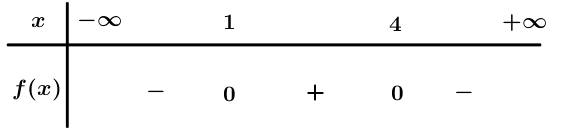
Dựa vào bảng xét dấu .
Câu 22:
12/07/2024Cho bất phương trình . Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: .
Bảng xét dấu
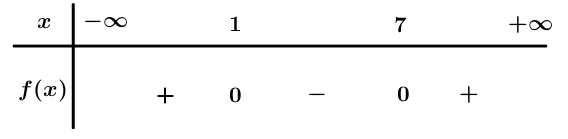
Dựa vào bảng xét dấu .
Tập nghiệm của bất phương trình là .
Vì và nên thỏa yêu cầu bài toán.
Câu 23:
19/07/2024Tập nghiệm của bất phương trình là
 Xem đáp án
Xem đáp án
Đáp án đúng là : A
Ta có: .
Bảng xét dấu
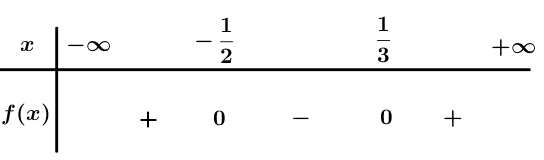
Dựa vào bảng xét dấu .
Câu 24:
19/07/2024Tập nghiệm S của bất phương trình + x - 12 < 0 là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tam thức bậc hai f(x) = + x - 12 có a = 1 > 0 và có hai nghiệm x = -4; x = 3. Ta có bảng xét dấu:
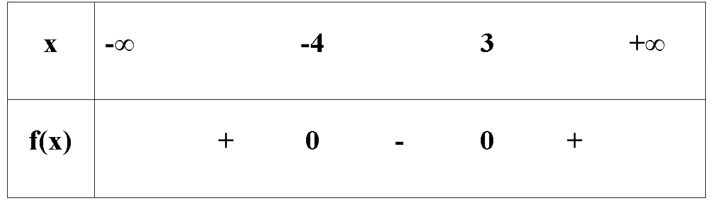
f(x) < 0 suy ra -4 < x < 3.
Câu 26:
12/07/2024Phương trình có tất cả bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Điều kiện xác định của phương trình
Từ phương trình đã cho ta được :
. Đối chiếu với điều kiện bài toán ta kết luận nghiệm của phương trình x =1.
Câu 27:
21/07/2024Tổng các nghiệm của phương trình bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Điều kiện xác định của phương trình
Ta có :
Giải phương trình
Vậy phương trình đã cho có hai nghiệm nên tổng hai nghiệm của phương trình là 1+2=3
Câu 28:
23/07/2024Nghiệm của phương trình là đáp án nào trong số các đáp án sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Điều kiện: x =
Bình phương hai vế của phương trình ta có: 3x - 4 = 4 - 3x6x = 8 x = .
Đối chiếu với điều kiện bài toán và thử lại kết quả suy ra phương trình có nghiệm
x = .
Câu 29:
22/07/2024Nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Điều kiện: x - 1 > 0x > 1.
Phương trình có thể viết lại như sau: = 0
. Xét điều kiện bài toán và thử lại kết quả suy ra phương trình có nghiệm
x = 4.
Câu 30:
22/07/2024Phương trình có nghiệm là?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Điều kiện:
Khi đó phương trình được viết thành:
= 0. Đối chiều với điều kiện bài toán và thử lại giá trị, ta thấy x = 1 là nghiệm của phương trình.
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài tập ôn tập chương 3 có đáp án (297 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Ôn tập chương 3 có đáp án (Phần 2) (528 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 Bài 1. Hàm số và Đồ thị có đáp án (871 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 4. Bất phương trình bậc hai một ẩn có đáp án (Phần 2) (783 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 5. Hai dạng phương trình quy về phương trình bậc hai có đáp án (Phần 2) (738 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng có đáp án (Phần 2) (717 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 1. Hàm số và đồ thị có đáp án (Phần 2) (606 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 3. Dấu của tam thức bậc hai có đáp án (Phần 2) (559 lượt thi)
- Trắc nghiệm Toán 10 Bài 2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng có đáp án (518 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Bất phương trình bậc hai một ẩn có đáp án (465 lượt thi)
- Trắc nghiệm Toán 10 Bài 5. Hai dạng đưa về phương trình bậc hai có đáp án (306 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Dấu của tam thức bậc hai có đáp án (0 lượt thi)
