• Logo VietJack.me
×
Trang chủ Lớp 11 Toán Trắc nghiệm Quy tắc đếm có đáp án (Thông hiểu)

Trắc nghiệm Quy tắc đếm có đáp án (Thông hiểu)

Trắc nghiệm Quy tắc đếm có đáp án (Thông hiểu)

  • 775 lượt thi

  • 15 câu hỏi

  • 30 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

19/07/2024

Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
Xem đáp án

Đáp án cần chọn là: B

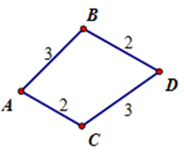
Số cách đi từ A đến D bằng cách đi từ A đến B rồi đến D là 3.2=6.

Số cách đi từ A đến D bằng cách đi từ A đến C rồi đến D là 2.3=6.

Áp dụng quy tắc cộng có : 6+6=12cách.

Câu 2:

21/07/2024

Số điện thoại ở Huyện Củ Chi có 7 chữ số và bắt đầu bởi 3 chữ số đầu tiên là 790. Hỏi ở Huyện Củ Chi có tối đa bao nhiêu máy điện thoại:
Xem đáp án

Đáp án cần chọn là: C

Gọi số điện thoại cần tìm có dạng 790abcd¯ .

Khi đó: a có 10 cách chọn, b có 10 cách chọn, c có 10 cách chọn, d có 10 cách chọn.

Theo quy tắc nhân, có tất cả 10.10.10.10 = 104 số.

Câu 3:

19/07/2024

Từ các chữ số 1,2,3,4,5,6,7 lập được bao nhiêu số tự nhiên gồm 4 chữ số khác nhau và là số chẵn?
Xem đáp án

Đáp án cần chọn là: A

Gọi số tự nhiên có 4 chữ số cần tìm là abcd¯ (a≠0,a≠b≠c≠d)

Vì abcd¯ là số chẵn nên d∈{2;4;6}

⇒ Có 3 cách chọn d.

Vì a≠d nên có 6 cách chọn a

b≠a,d nên có 5 cách chọn b

c≠a,b,d nên có 4 cách chọn c

Áp dụng quy tắc nhân ta có số các số thỏa mãn là: 3.6.5.4=360 (số).

Chú ý

Đối với bài toán này, vì số cần lập là số chẵn nên ta ưu tiên chọn dd trước rồi mới đến các chữ số khác.

Câu 4:

19/07/2024

Có bao nhiêu cách sắp xếp 8 viên bi đỏ khác nhau và 8 viên bi đen khác nhau thành một dãy sao cho hai viên bi cùng màu không được ở cạnh nhau?
Xem đáp án

Đáp án cần chọn là: A

Do hai viên bi cùng màu không được đứng cạnh nhau nên ta có trường hợp sau:

Trường hợp 1: Các viên bi đỏ ở vị trí lẻ.

Có 8  cách chọn viên bi đỏ ở vị trí 1.

Có 7 cách chọn viên bi đỏ ở vị trí 3.

...

Có 11  cách chọn viên bi đỏ ở vị trí 15.

Suy ra có 8.7.6.5.4.3.2.1 =  40320 cách xếp viên bi đỏ.

Tương tự có 8.7.6.5.4.3.2.1= 40320  cách xếp viên bi xanh.

Vậy có 40320. 40320 =  1625 702 400 cách xếp.

Trường hợp 2: Các viên bi đỏ ở vị trí chẵn ta cũng có cách xếp tương tự.

Vậy theo quy tắc cộng ta có: 2. 1625 702 400=3251404800.

Chú ý

Một số em có thể sẽ chọn nhầm đáp án B vì chỉ xét có 1 trường hợp là sai.

Câu 5:

17/07/2024

Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ.
Xem đáp án

Đáp án cần chọn là: B

Chọn vị trí cho hai nhóm 3 nam và 3 nữ có 2 cách chọn (1 nhóm ở vị trí chẵn và nhóm còn lại ở vị trí lẻ)

Xếp 3 nam có: 3.2.1 cách xếp.

Xếp 3 nữ có: 3.2.1 cách xếp.

Vậy có 2. 3.2.12 = 72 cách xếp.

Câu 6:

21/07/2024

Trên giá sách có 10 quyển Văn khác nhau, 8 quyển sách Toán khác nhau và 6 quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?
Xem đáp án

Đáp án cần chọn là: D

Theo quy tắc nhân ta có:

Trường hợp 1: Chọn một quyển Văn và một quyển Toán khác nhau.

Theo quy tắc nhân có: 10.8=80 cách

Trường hợp 2: chọn một quyển Văn và một quyển Tiếng Anh khác nhau.

Theo quy tắc  nhân có:  10.6=60 cách

Trường hợp 3: chọn một quyển Toán và một quyển Tiếng Anh khác nhau.

 Có: 8.6=48 cách

Theo quy tắc cộng ta có số cách chọn hai quyển sách khác môn là:  80+60+48=188 cách.

Chú ý

Sau khi tính xong số cách cho mỗi trường hợp, một số em có thể sẽ áp dụng nhầm công thức nhân dẫn đến chọn nhầm đáp án A.

Câu 7:

19/07/2024

Trên giá sách có 6 quyển Văn khác nhau, 5 quyển sách Toán khác nhau và 9 quyển sách Tiếng Anh khác nhau. Hỏi có bao nhiêu cách chọn hai quyển sách khác môn?
Xem đáp án

Đáp án cần chọn là: D

Trường hợp 1: chọn một quyển Văn và một quyển Toán khác nhau.

Có:  6.5=30 cách

Trường hợp 2; chọn một quyển Văn và một quyển Tiếng Anh khác nhau.

Có 6.9=54 cách

Trường hợp 3: chọn một quyển Toán và một quyển Tiếng Anh khác nhau.

 Có 5.9=45 cách

Theo quy tắc cộng ta có số cách chọn hai quyển sách khác môn là: 30+54+45=129 cách.

Câu 8:

21/07/2024

Biển đăng kí xe ô tô có 6  chữ số và hai chữ cái trong 26  chữ cái (không dùng các chữ I và O ). Chữ số đầu tiên khác 0. Hỏi số ô tô được đăng kí nhiều nhất có thể là bao nhiêu?
Xem đáp án

Đáp án cần chọn là: A

Theo quy tắc nhân ta thực hiện từng bước.

Chữ cái đầu tiên có 24 cách chọn  ( vì không dung chữ I và O).

Chữ cái tiếp theo cũng có 24 cách chọn.

Chữ số đầu tiên có 9 cách chọn.

Chữ số thứ hai có 10 cách chọn.

Chữ số thứ ba có 10 cách chọn.

Chữ số thứ tư có 10 cách chọn.

Chữ số thứ năm có 10 cách chọn.

Chữ số thứ sáu có 10 cách chọn.

Vậy theo quy tắc nhân ta có 24.24.9. 105 =5184.105 là số ô tô nhiều nhất có thể đăng kí.

Câu 9:

19/07/2024

Cho các số 1,2,3,4,5,6,7. Số các số tự nhiên gồm 5 chữ số lấy từ 7 chữ số trên sao cho chữ số đầu tiên bằng 3 là:
Xem đáp án

Đáp án cần chọn là: D

Gọi số cần tìm có dạng : abcde¯

Chọn a : có 1 cách ( vì a=3)

Chọn b: có 7 cách

Chọn c: có 7 cách

Chọn d:  có 7 cách

Theo quy tắc nhân, có 1.7.7.7.7 =2401 (số)

Câu 10:

21/07/2024

Có bao nhiêu số tự nhiên có 5 chữ số trong đó các chữ số cách đều chữ số đứng giữa thì giống nhau?
Xem đáp án

Đáp án cần chọn là: A

Gọi số cần tìm là abcba¯

Có 9  cách chọn a ( vì a khác 0)

Có 10 cách chọn b .

Có 10 cách chọn c .

Vậy có 9.10.10 = 900 số.

Câu 11:

22/07/2024

Một dãy ghế dài có 10 ghế. Xếp một cặp vợ chồng ngồi vào 2 trong 10 ghế sao cho người vợ ngồi bên phải người chồng (không bắt buộc ngồi gần nhau). Số cách xếp là:
Xem đáp án

Đáp án cần chọn là: A

Ta lần lượt đánh số các ghế từ 1 đến 10.

Nếu người chồng ngồi ở vị trí 1 thì có 9 cách xếp người vợ.

Nếu người chồng ngồi ở vị trí 2 thì có 8 cách xếp người vợ.

….

Nếu người chồng ngồi ở vị trí 9 thì có 1 cách xếp người vợ.

Nếu người chồng ngồi ở vị trí 10 thì có 0 cách xếp người vợ.

Vậy có tất cả 9+8+7+6+5+4+3+2+1=45 cách.

Câu 12:

22/07/2024

Cho tập hợp A=2;3;5;8. Từ  tập A có thể lập bao nhiêu số tự nhiên x sao cho 400<x<600?
Xem đáp án

Chọn đáp án D

Số tự nhiên x có dạng abc¯ với a,b,c∈A.

Vì 400<x<600 nên a=5

Chọn  b có 4 cách

Chọn c có 4 cách

Số số tự nhiên thỏa mãn là: 1.4.4 = 16.

Câu 13:

20/07/2024

Cho tập hợp A=0;1;2;3;4;5 . Có thể lập bao nhiêu số tự nhiên có 3 chữ số khác nhau và chia hết cho 5?
Xem đáp án

Chọn đáp án D

Số tự nhiên x có dạng abc¯ với a,b,c∈A và đôi một phân biệt.

Vì số tạo ra chia hết cho 5 nên c∈0;5.

+) Với c= 0

Thì a có 5 cách chọn, b có 4 cách chọn ⇒ 5.4 = 20 số.

+) Với c=5,

Chọn  a có 4 cách (Vì a≠0; a≠c )

Chọn b có 4 cách ( Vì b≠a; b≠c)

Trong trường hợp này có:  1. 4.4 = 16 số

Vậy có tất cả: 20+16=36 số.

Câu 14:

21/07/2024

Có bao nhiêu số tự nhiên chẵn gồm hai chữ số khác nhau được lập từ các chữ số 0, 1, 2, 3, 4, 5?
Xem đáp án

Chọn đáp án C

Số tự nhiên thỏa mãn có dạng ab¯. Vì số cần lập là số chẵn nên b∈0;2;4

+) Với b=0⇒a∈1;2;3;4;5⇒ 5 số.

+) Với b≠0⇒b có 2 cách chọn là 2, 4; a có 4 cách chọn ⇒ 2.4 = 8 số.

Vậy có tất cả: 8 + 5 = 13 số.

Câu 15:

19/07/2024

Cho hai đường thẳng a và b song song với nhau. Trên đường thẳng a có 10 điểm phân biệt, trên đường thẳng b có 8 điểm phân biệt.Hỏi từ các điểm đã cho lập được bao nhiêu tam giác?
Xem đáp án

Chọn đáp án A.

+ Trường hợp 1: Tam giác đươc tạo ra có 2 điểm thuộc đường thẳng a và 1 điểm thuộc đường thẳng b..

Có: 10.9 = 90 cách chọn 2 điểm thuộc đường thẳng a

Và có 8 cách chọn 1 điểm thuộc đường thẳng b

Trong trường hợp này có: 90.8 = 720 cách

+ Trường hợp 2: Tam giác được tạo thành có 1 điểm thuộc a và 2 điểm thuộc đường thẳng b

Có 10 cách chọn 1 điểm thuộc a

Và 8.7 = 56 cách chọn 2 điểm thuộc b

Trong trường hợp này có: 10.56 = 560 cách

Theo quy tắc cộng có:  720+560 = 1280 tam giác

Bắt đầu thi ngay

Có thể bạn quan tâm

Các bài thi hot trong chương