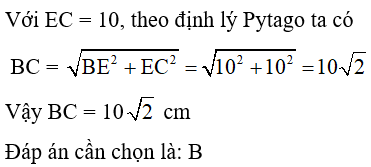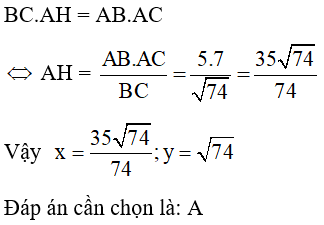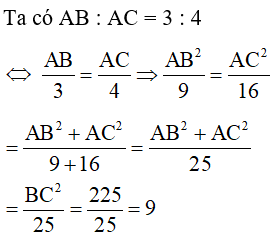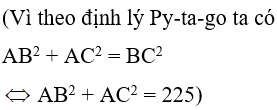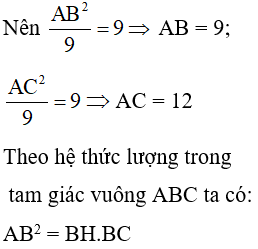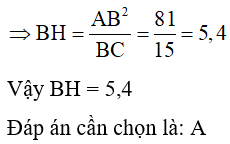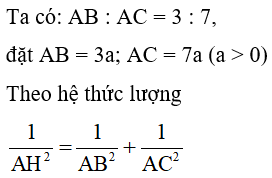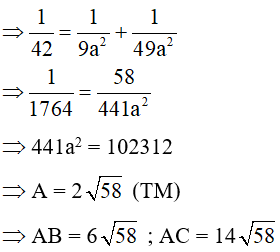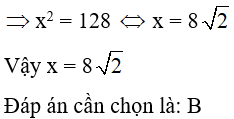Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án)
Trắc nghiệm Toán 9 Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông
-
633 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 2:
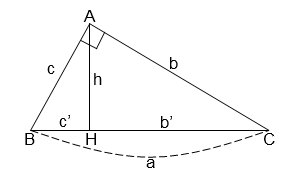
20/07/2024Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
 Xem đáp án
Xem đáp án
Nhận thấy ah = bc nên phương án C là sai
Đáp án cần chọn là: C
Câu 4:
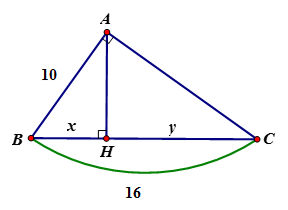
23/07/2024Tìm x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AB2 = BH.BC
CH = BC – BH = 16 – 6,25 = 9,75
Vậy x = 6,25; y = 9,75
Đáp án cần chọn là: B
Câu 5:
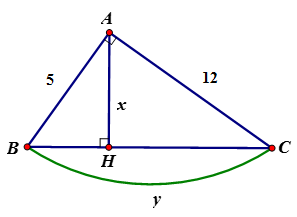
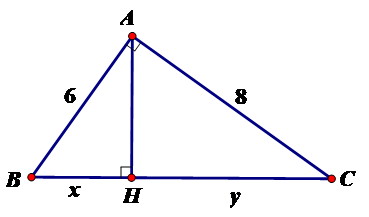
23/07/2024Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Theo định lý Py-ta-go ta có
BC2 = AB2 + AC2
BC2 = 100 BC = 10
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AB2 = BH.BC
hay x = 3,6
CH = BC – BH = 10 – 3,6 = 6,4
Đáp án cần chọn là: A
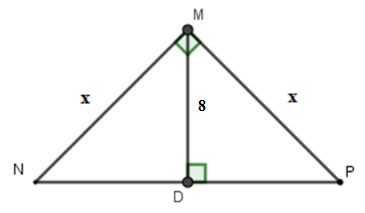
Câu 6:
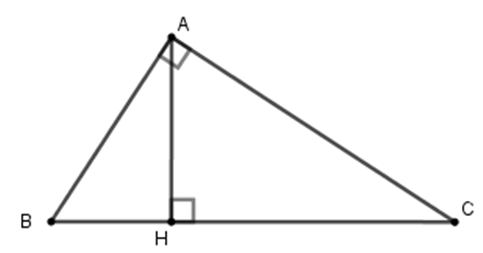
23/07/2024Cho tam giác ABC vuông tại A, AHBC (H thuộc BC).
Cho biết AB : AC = 4 : 5 và BC = cm.
Tính độ dài đoạn thẳng CH (làm tròn đến chữ số thập phân thứ nhất).
 Xem đáp án
Xem đáp án
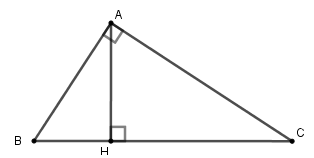
Ta có AB : AC = 4 : 5
(Vì theo định lý Py-ta-go ta có
AB2 + AC2 = BC2
AB2 + AC2 = (√41)2= 41)
Nên AB2 = 16
AB = 4; AC225=1⇒AC = 5
Theo hệ thức lượng trong tam giác vuông ABC ta có:
AC2 = CH.BC
Vậy CH3,9
Đáp án cần chọn là: D
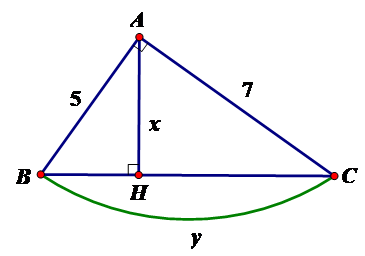
Câu 7:
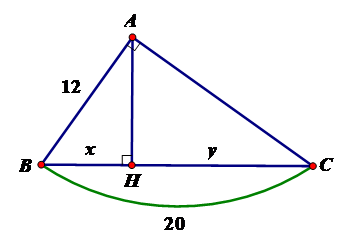
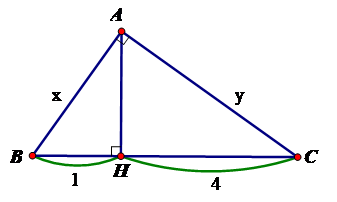
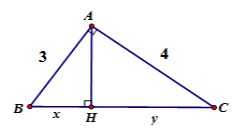
21/07/2024Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Theo định lý Py-ta-go ta có
BC2 = AB2 + AC2
BC2 = 25 BC = 5
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
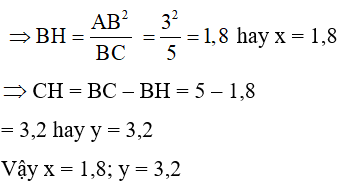
Đáp án B
Câu 8:
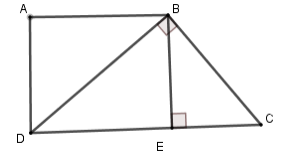
07/12/2024Tính diện tích hình thang ABCD có đường cao bằng 12cm, hai đường chéo AC và BD vuông góc với nhau, BD = 15cm.
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải
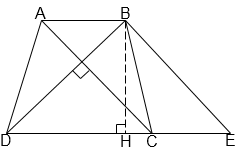
Qua B vẽ đường thẳng song song với AC, cắt DC ở E.
Gọi BH là đường cao của hình thang.
Ta có BE // AC, ACBD nên BEBD
Áp dụng định lý Pytago vào tam giác vuông BDH,
ta có: BH2 + HD2 = BD2
122 + HD2 = 152
HD2 = 81HD = 9cm
Xét tam giác BDE vuông tại B:
BD2 = DE.DH152 = DE.9
DE = 25cm
Ta có: AB = CE nên:
AB + CD = CE + CD = DE = 25cm
Do đó SABCD = 25.12 : 2 = 150(cm2)
*Phương pháp giải:
Sử dụng định lý Pytago tính HD
Sử dụng hệ thức lượng trong tam giác vuông tính DE
Diện tích hình thang bằng tích của tổng hai đáy với chiều cao chia 2.
*Lý thuyết :
a) Định nghĩa
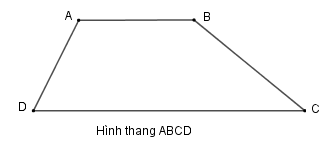
Hình thang ABCD có:
- Cạnh đáy AB và cạnh đáy DC. Cạnh bên AD và cạnh bên BC.
- Hai cạnh đáy là hai cạnh đối diện song song.
Hình thang có một cặp cạnh đối diện song song.
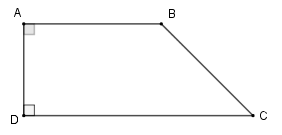
Chú ý: Hình thang có một cạnh bên vuông góc với hai đáy gọi là hình thang vuông.
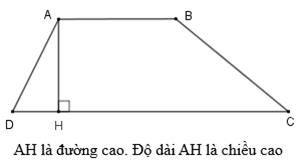
b) Đường cao của hình thang
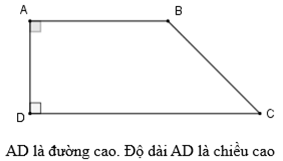
2. Diện tích hình thang
Quy tắc: Diện tích hình thang bằng tổng độ dài hai đáy nhân với chiều cao (cùng một đơn vị đo) rồi chia cho 2.
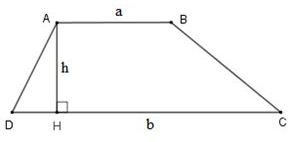
(S là diện tích; a, b là độ dài các cạnh đáy; h là chiều cao)
Xem thêm
35 Bài tập Hình thang. Diện tích hình thang lớp 5 (có đáp án)
Câu 9:
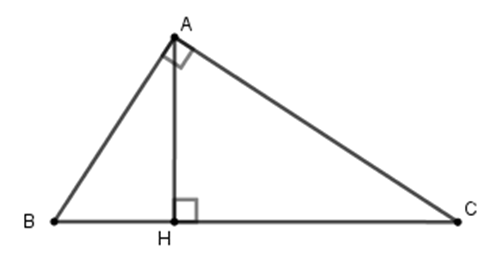
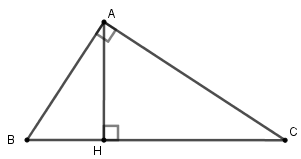
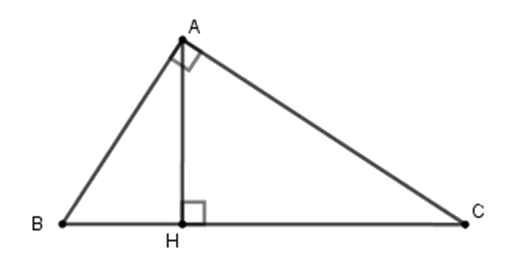
23/07/2024Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức
HA2 = HB.HC
Đáp án cần chọn là: B
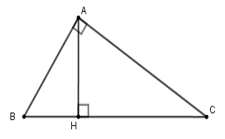
Câu 10:
23/07/2024Cho tam giác ABC vuông tại A, đường cao AH. Biết AB : AC = 3 : 4 và AB + AC = 21
 Xem đáp án
Xem đáp án
Theo giả thiết AB : AC = 3 : 4
Suy ra
Do đó AB = 3.3 = 9 (cm);
AC = 3.4 = 12 (cm)
Tam giác ABC vuông tại A,
theo định lý Pytago ta có:
BC2 = AB2 + AC2 = 92 + 122 = 225,
suy ra BC = 15cm
Đáp án cần chọn là: B
Câu 11:
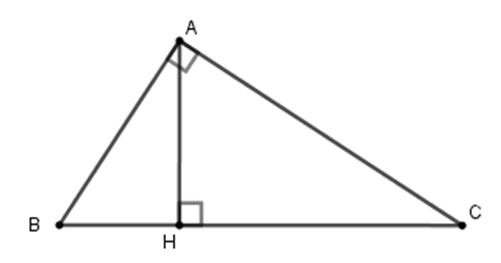
22/07/2024Cho tam giác ABC vuông tại A, đường cao AH (như hình vẽ). Hệ thức nào sau đây là sai?
 Xem đáp án
Xem đáp án
Cho tam giác ABC vuông tại A,
đường cao AH. Khi đó ta có hệ thức

Câu 15:
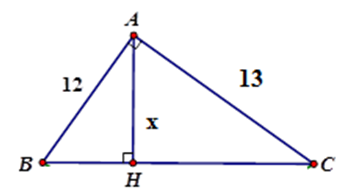
20/07/2024Tìm x trong hình vẽ sau (làm tròn đến chữ số thập phân thứ hai).
 Xem đáp án
Xem đáp án
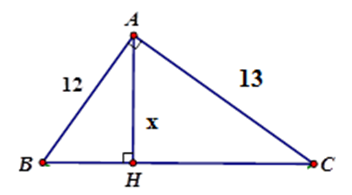
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
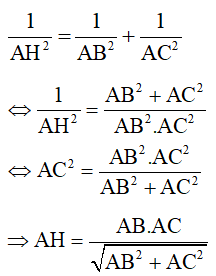
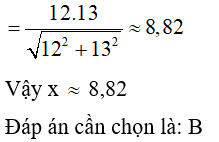
Câu 16:
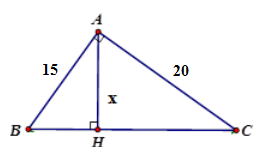
22/07/2024Tính x trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
Vậy x = 12
Đáp án cần chọn là: C
Câu 17:
22/07/2024Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng…”. Cụm từ thích hợp điền vào chỗ trống là:
 Xem đáp án
Xem đáp án
Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có hệ thức
HA2 = HB.HC
Hay “Trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng Tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền”
Đáp án cần chọn là: B
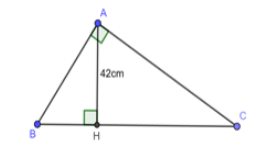
Câu 18:
23/07/2024Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết AH = 4cm, . Tính chu vi tam giác ABC?
 Xem đáp án
Xem đáp án
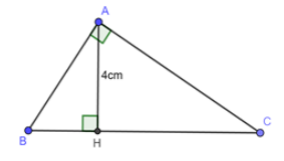
Ta có: HC = 4HB



Câu 21:
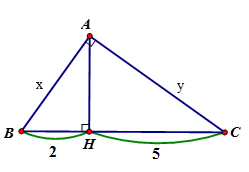
23/07/2024Tính x, y trong hình vẽ sau:
 Xem đáp án
Xem đáp án
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
AH2 = BH.CH
AH2 = 2.5AH =√10
Áp dụng định lý Pytago cho tam giác vuông AHB, AHC ta có
AB = ;
AC =
Vậy x = ; y =√15
Đáp án cần chọn là: A
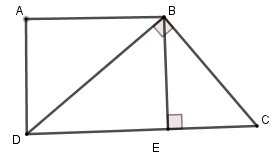
Câu 25:
21/07/2024Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 9cm, CH = 16cm. Gọi D, E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC. Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N (hình vẽ).
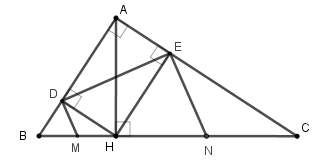
Tính độ dài đoạn thẳng DE.
 Xem đáp án
Xem đáp án

Nên DE = 12cm
Đáp án cần chọn là: A
Có thể bạn quan tâm
- Trắc nghiệm Một số hệ thức về cạnh và đường cao trong tam giác vuông (có đáp án) (632 lượt thi)
- Bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông (928 lượt thi)
Các bài thi hot trong chương
- Bài 2: Tỉ số lượng giác của góc nhọn (2106 lượt thi)
- Bài 4: Một số hệ thức về cạnh và góc trong tam giác vuông (1312 lượt thi)
- Ôn tập chương 1 Hình học (1204 lượt thi)
- Bài 5. Ứng dụng thực tế các tỉ số lượng giác của góc nhọn (772 lượt thi)
- Trắc nghiệm Một số hệ thức về cạnh và góc trong tam giác vuông (có đáp án) (657 lượt thi)
- Trắc nghiệm Ôn tập chương 1 Hình học (có đáp án) (427 lượt thi)
- Trắc nghiệm Tỉ số lượng giác của góc nhọn và Bảng lượng giác (có đáp án) (412 lượt thi)