Top 8 Đề kiểm tra Toán 12 Chương 1 Hình học có đáp án
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 6)
-
3503 lượt thi
-
14 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Có bao nhiêu khối đa diện đều?
 Xem đáp án
Xem đáp án
Chọn B.
Có 5 khối đa diện đều là: tứ diện đều, hình lập phương, khối 8 mặt đều, khối 12 mặt đều, khối 20 mặt đều.
Câu 2:
20/07/2024Khái niệm nào sau đây đúng với khối chóp?
 Xem đáp án
Xem đáp án
Chọn B.
+ Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thoả mãn hai tính chất:
* Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
* Mỗi cạnh của đa giác là cạnh chung của đúng hai đa giác.
+ Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó. Vậy khi đọc vào từng đáp án ở đây thì ta thấy ý A chính là khái niệm của hình chóp. Ý B là khái niệm của khối chóp. Ý C là mệnh đề bị thiếu, ý D sai.
Câu 4:
23/07/2024Hình chóp tứ giác đều có mấy trục đối xứng?
 Xem đáp án
Xem đáp án
Chọn B
Hình chóp tứ giác đều có 1 trục đối xứng đó là trục của đường tròn ngoại tiếp đáy.
Câu 6:
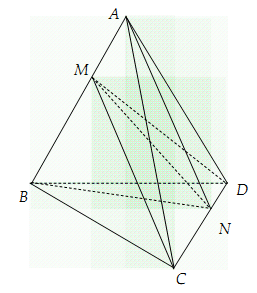
21/07/2024Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành 4 khối tứ diện:
 Xem đáp án
Xem đáp án
Chọn A.
Nhìn vào hình vẽ ta thấy MN là giao tuyến của hai mặt phẳng (MCD) và (NAB), khi đó ta thấy tứ diện đã cho được chia thành bốn tứ diện ACMN,AMND,BMNC,BMND.
Câu 7:
14/07/2024Số mặt phẳng đối xứng của tứ diện đều là:
 Xem đáp án
Xem đáp án
Chọn C.
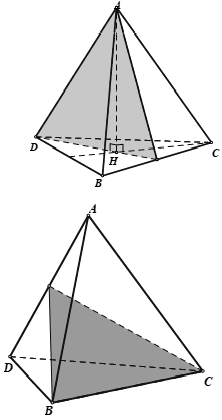
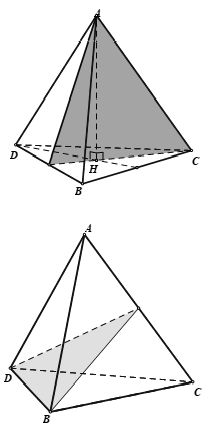
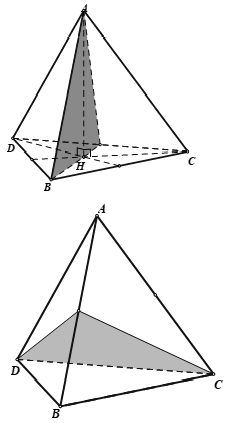
Tứ diện đều có mặt phẳng đối xứng là mặt phẳng tạo bởi một cạnh với trung điểm của cạnh đối diện của nó.
Câu 8:
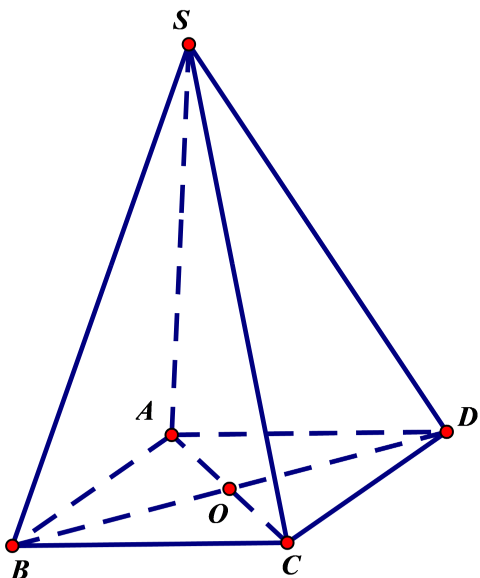
20/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có 1 mặt phẳng đối xứng là?
 Xem đáp án
Xem đáp án
Chọn A.
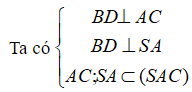
![]()
Suy ra (SAC) là mặt phẳng trung trực của BD.
Suy ra (SAC) là mặt đối xứng của hình chóp, và đây là mặt phẳng duy nhất.
Câu 9:
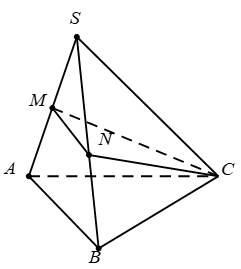
14/07/2024Cho hình chóp S.ABC, gọi M; N lần lượt là trung điểm của SA; SB. Tính tỉ số
 Xem đáp án
Xem đáp án
Chọn B
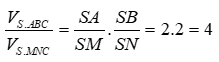
Câu 10:
27/11/2024Tính thể tích khối tứ diện đều cạnh a?
 Xem đáp án
Xem đáp án
Đáp án đúng: A.
*Lời giải:
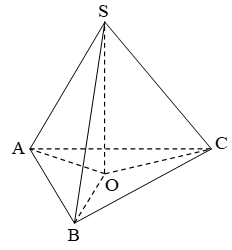
Gọi tứ diện SABC đều cạnh a.
Gọi O là hình chiếu của S lên (ABC).
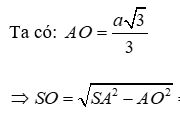
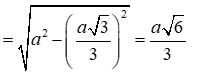
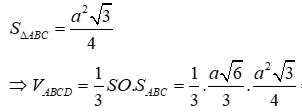
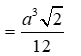
*Phương pháp giải:
Thể tích: V = 1/3. B .h
( B là diện tích tam giác đáy )
*Lý thuyết nắm thêm về khối đa diện
Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
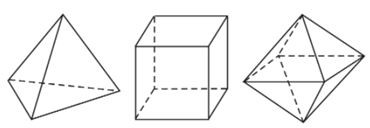
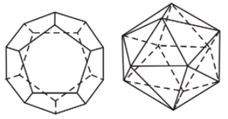
Bảng tóm tắt của năm loại khối đa diện đều.

Thể tích của khối lăng trụ.
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
Thể tích khối chóp.
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: V=13B.hV=13B.h.
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Khối đa diện lồi và khối đa diện đều (mới 2024 + Bài Tập) – Toán 12
50 Bài tập Khối đa diện lồi và khối đa diện đều Toán 12 mới nhất
Câu 11:
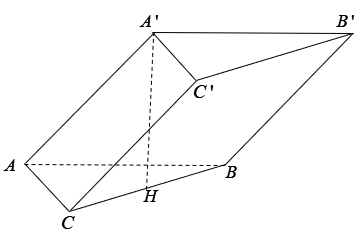
22/07/2024Cho lăng trụ ABC.A'B'C' có ABC là tam giác vuông tại A. Hình chiếu của A’ lên (ABC) là trung điểm của BC. Tính thể tích khối lăng trụ ABC.A'B'C' biết
 Xem đáp án
Xem đáp án
Chọn B.
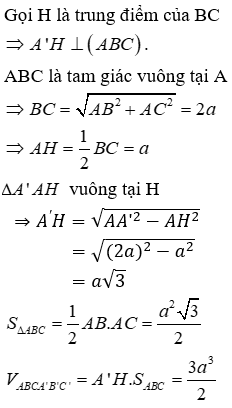
Câu 12:
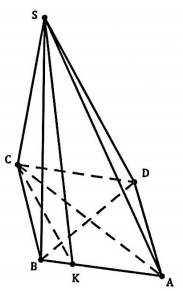
17/07/2024Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chop S.ABCD.
 Xem đáp án
Xem đáp án
Chọn D.
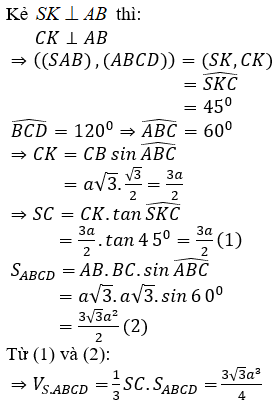
Câu 13:
21/07/2024Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
 Xem đáp án
Xem đáp án
Chọn A.
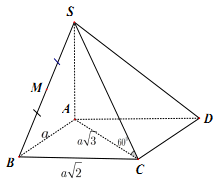
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD)
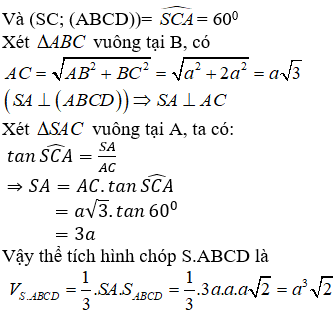
Câu 14:
23/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.
 Xem đáp án
Xem đáp án
Chọn A.
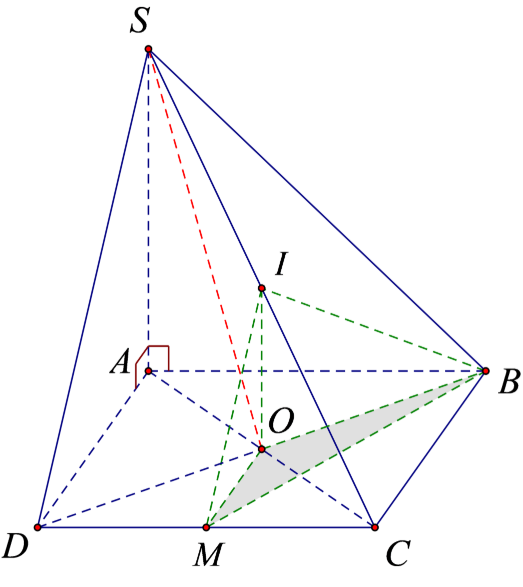
Do IO là đường trung bình của tam giác SAC nên:
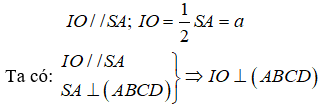
* OM là đường trung bình tam giác ACD nên:
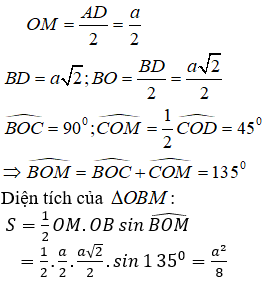
Tính thể tích của khối chóp I.OBM:
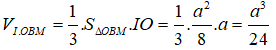
Bài thi liên quan
-
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 1)
-
10 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 2)
-
15 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 3)
-
3 câu hỏi
-
30 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 4)
-
3 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 5)
-
14 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 7)
-
12 câu hỏi
-
20 phút
-
-
Đề kiểm tra 15 phút Toán 12 Chương 1 Hình học có đáp án (Đề 8)
-
11 câu hỏi
-
20 phút
-
Có thể bạn quan tâm
- Đề kiểm tra 1 tiết Giải tích 12 Chương 1 có đáp án (419 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 1 Giải tích có đáp án (2249 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 chương 2 có đáp án (290 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 2 Giải tích có đáp án (2256 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 1 Hình học có đáp án (3502 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 2 Hình học có đáp án (2485 lượt thi)
- Top 4 Đề thi Toán lớp 12 Học kì 1 chọn lọc, có đáp án (2897 lượt thi)
Các bài thi hot trong chương
- Top 8 Đề kiểm tra Toán 12 Chương 3 Hình học có đáp án (2228 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 3 Giải tích có đáp án (2107 lượt thi)
- Top 8 Đề kiểm tra Toán 12 Chương 4 Giải tích có đáp án (1689 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 Chương 3 có đáp án (387 lượt thi)
- Đề thi Học kì 2 Giải tích 12 có đáp án (319 lượt thi)
- Đề kiểm tra 1 tiết Giải tích 12 Chương 4 có đáp án (299 lượt thi)
