Câu hỏi:
27/11/2024 181Tính thể tích khối tứ diện đều cạnh a?
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A.
*Lời giải:
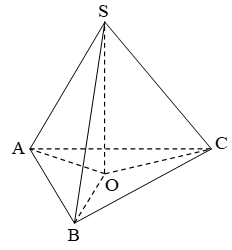
Gọi tứ diện SABC đều cạnh a.
Gọi O là hình chiếu của S lên (ABC).
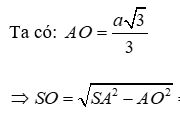
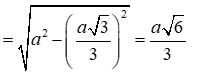
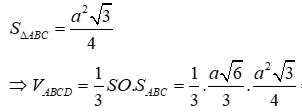
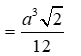
*Phương pháp giải:
Thể tích: V = 1/3. B .h
( B là diện tích tam giác đáy )
*Lý thuyết nắm thêm về khối đa diện
Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
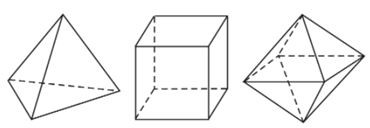
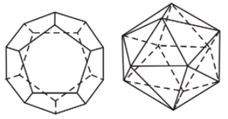
Bảng tóm tắt của năm loại khối đa diện đều.

Thể tích của khối lăng trụ.
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
Thể tích khối chóp.
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: .
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Khối đa diện lồi và khối đa diện đều (mới 2024 + Bài Tập) – Toán 12
50 Bài tập Khối đa diện lồi và khối đa diện đều Toán 12 mới nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
Câu 3:
Cho khối tứ diện ABCD. Lấy một điểm M nằm giữa A và B, một điểm N nằm giữa C và D bằng hai mặt phẳng (MCD) và (NAB) ta chia khối tứ diện đã cho thành 4 khối tứ diện:
Câu 4:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a, SA vuông góc với (ABCD) và SA = 2a. Gọi I là trung điểm của SC và M là trung điểm của DC. Tính thể tích của khối chóp I.OBM.
Câu 6:
Cho hình chóp S.ABCD có SC ⊥ (ABCD), đáy ABCD là hình thoi có cạnh bằng . Biết rằng góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 45°. Tính theo a thể tích khối chop S.ABCD.
Câu 10:
Cho hình chóp S.ABC, gọi M; N lần lượt là trung điểm của SA; SB. Tính tỉ số
Câu 11:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA vuông góc với (ABCD). Hình chóp này có 1 mặt phẳng đối xứng là?
Câu 12:
Cho lăng trụ ABC.A'B'C' có ABC là tam giác vuông tại A. Hình chiếu của A’ lên (ABC) là trung điểm của BC. Tính thể tích khối lăng trụ ABC.A'B'C' biết


