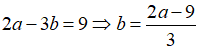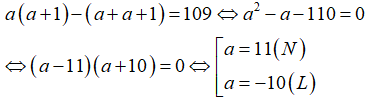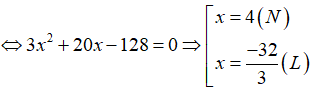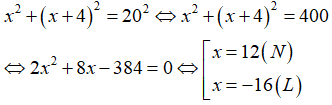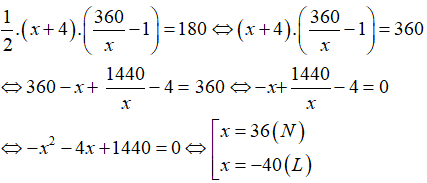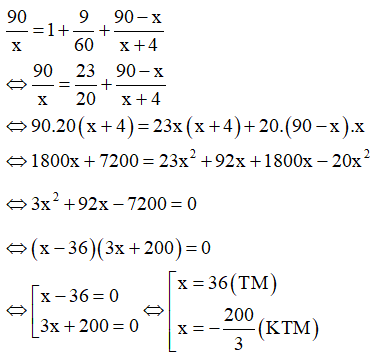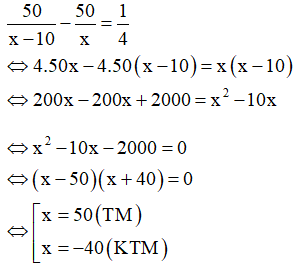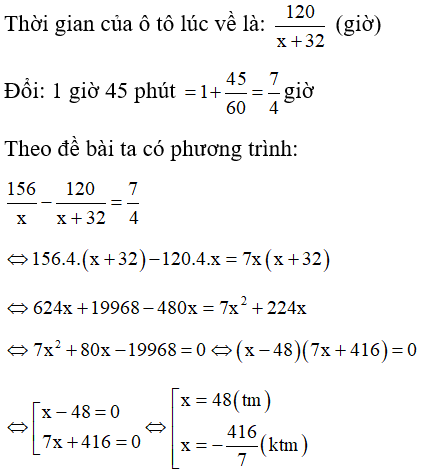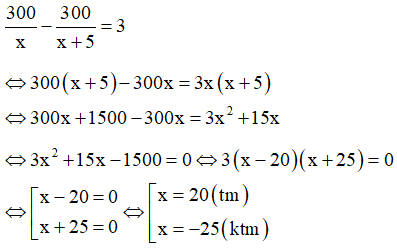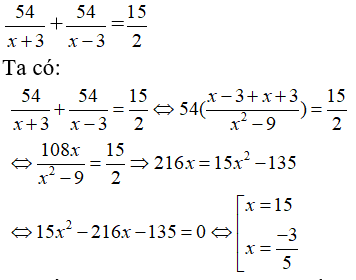Trắc nghiệm Toán 9 Bài 8 (có đáp án): Giải bài toán bằng cách lập phương trình
-
1122 lượt thi
-
10 câu hỏi
-
20 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho hai số tự nhiên biết rằng hai lần số thứ nhất hơn ba lần số thứ hai là 9 và hiệu các bình phương của chúng bằng 119. Tìm số lớn hơn.
Xem đáp án
Đáp án A
Gọi số thứ nhất là a; a N , số thứ hai là b; b N
Vì hai lần số thứ nhất hơn ba lần số thứ hai là 9 nên ta có:
Vì hiệu các bình phương của chúng bằng 119 nên ta có phương trình:
hay
Nên phương trình có hai nghiệm
Câu 2:
23/07/2024Tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109. Tìm số bé hơn.
Xem đáp án
Đáp án D
Gọi số bé hơn là a; a N thì số lớn hơn là a + 1
Vì tích của hai số tự nhiên liên tiếp lớn hơn tổng của chúng là 109 nên ta có phương trình:
Vậy số bé hơn là 11.
Câu 3:
03/11/2024Một hình chữ nhật có chiều dài gấp 3 lần chiều rộng. Nếu cả chiều dài và chiều rộng cùng tăng thêm 5cm thì được một hình chữ nhật mới có diện tích bằng 153 . Tìm chu vi hình chữ nhật ban đầu.
Xem đáp án
Đáp án đúng: B
*Lời giải
Gọi x là chiều rộng hình chữ nhật lúc đầu (x > 0) (cm)
Chiều dài hình chữ nhật lúc đầu: 3x (cm)
Chiều rộng hình chữ nhật lúc sau: x + 5 (cm)
Chiều dài hình chữ nhật lúc sau: 3x + 5 (cm)
Theo đề bài ta có phương trình: (x + 5)(3x + 5) = 153
Vậy chiều dài và chiều rộng hình chữ nhật ban đầu là: 12 cm và 4 cm
Suy ra chu vi hình chữ nhật ban đầu là: (12 + 4).2 = 32 (cm)
*Phương pháp giải
Bài toán về diện tích hình học
Bước 1: Lập phương trình.
- Chọn ẩn và đặt điều kiện cho ẩn (nếu có).
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: So sánh với điều kiện và kết luận.
*Lý thuyến cần nắm và các dạng bài về giải bài toán bằng cách lập phương trình:
Các bước giải bài toán bằng cách lập phương trình
Bước 1: Lập phương trình
- Chọn ẩn và đặt điều kiện thích hợp cho chúng
- Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình nói trên.
Bước 3: Trả lời: Kiểm tra xem trong các nghiệm của phương trình, nghiệm nào thỏa mãn điều kiện và kết luận.
Bài toán năng suất
Bước 1: Lập phương trình.
- Chọn ẩn và đặt điều kiện cho ẩn (nếu có).
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: So sánh với điều kiện và kết luận.
Công việc = Năng xuất x Thời gian
Bài toán chuyển động
Bước 1: Lập phương trình.
- Chọn ẩn và đặt điều kiện cho ẩn (nếu có).
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: So sánh với điều kiện và kết luận.
Quãng đường = Vận tốc x Thời gian
Bài toán về diện tích hình học
Bước 1: Lập phương trình.
- Chọn ẩn và đặt điều kiện cho ẩn (nếu có).
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: So sánh với điều kiện và kết luận.
Một số công thức tính diện tích thường gặp:
Diện tích tam giác: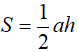 
(a là độ dài cạnh đáy, h là độ dài đường cao ứng với cạnh đáy).
Diện tích hình vuông: S = a2 (a là độ dài cạnh góc vuông).
Diện tích hình chữ nhật: S = ab (a, b là chiều dài, chiều rộng của hình chữ nhật).
Diện tích hình tròn: S = πR2 (R là bán kính của hình tròn).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giải bài toán bằng cách lập phương trình (mới 2024 + Bài Tập) – Toán 9
50 Bài tập Giải bài toán bằng cách lập phương trình Toán 9 mới nhất
Câu 4:
18/07/2024Cho tam giác vuông có cạnh huyền bằng 20 cm. Hai cạnh góc vuông có độ dài hơn kém nhau 4 cm. Một trong hai cạnh góc vuông của tam giác vuông có độ dài là:
Xem đáp án
Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm
Câu 5:
23/07/2024Một thửa ruộng hình tam giác có diện tích 180 . Tính chiều dài cạnh đáy thửa ruộng, biết rằng nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm đi 1m thì diện tích không đổi.
Xem đáp án
Đáp án C
Gọi độ dài cạnh đáy là x (cm) (x > 0)
Chiều cao của thửa ruộng có độ dài là: 360/x (cm)
Vì nếu tăng cạnh đáy lên 4m và chiều cao tương ứng giảm 1m đi thì diện tích không đổi nên ta có phương trình:
Vậy chiều dài cạnh đáy của thửa ruộng có độ dài là: 36 cm
Câu 6:
23/07/2024Một người dự định đi xe máy từ tỉnh A đến tỉnh B cách nhau 90 km trong một thời gian đã định. Sau khi đi được 1 giờ, người đó nghỉ 9 phút. Do đó, để đến tỉnh B đúng hẹn, người ấy phải tăng vận tốc thêm 4 km/h. Tính vận tốc lúc đầu của người đó.
Xem đáp án
Đáp án A
Gọi vận tốc ban đầu của người đó là x (km/h) (x > 0).
Thời gian dự định người đó đi hết quãng đường là 90/x (h).
Quãng đường người đó đi được sau 1 giờ là x (km).
Quãng đường còn lại người đó phải tăng tốc là 90 – x (km).
Vận tốc của người đó sau khi tăng tốc là x + 4 (km/h).
Thời gian người đó đi hết quãng đường còn lại là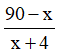 
(h).
Theo đề bài ta có phương trình:
Vậy vận tốc lúc đầu của người đó là 36 km/h.
Câu 7:
23/07/2024Quãng đường AB dài 50 km. Hai xe máy khởi hành cùng một lúc từ A đến B. Vận tốc xe thứ nhất lớn hơn vận tốc xe thứ hai 10 km/h, nên xe thứ nhất đến B trước xe thứ hai 15 phút. Tính vận tốc mỗi xe.
Xem đáp án
Đáp án B
Gọi vận tốc của xe thứ nhất là x (km/h) (x > 10).
Vận tốc của xe thứ hai là x – 10 (km/h).
Thời gian xe thứ nhất đi từ A đến B là 50/x (h).
Thời gian xe thứ hai đi từ A đến B là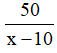 
(h).
Vì xe thứ nhất đến B trước xe thứ hai 15 phút = 1/4 h nên ta có phương trình:
Vậy vận tốc của xe thứ nhất là 50 km/h, vận tốc của xe thứ hai là 40 km/h.
Câu 8:
19/11/2024Một xe ô tô đi từ A đến B theo đường quốc lộ cũ dài 156km với vận tốc không đổi. Khi từ B về A, xe đi đường cao tốc mới nên quãng đường giảm được 36km so với lúc đi và vận tốc tăng so với lúc đi là 32km/h. Tính vận tốc ô tô khi đi từ A đến B, biết thời gian đi nhiều hơn thời gian về là 1 giờ 45 phút.
Xem đáp án
Đáp án đúng là D
Lời giải
Gọi vận tốc của ô tô khi đi từ A đến B là x (km/h) (x > 0)
Thời gian ô tô đi từ A đến B là: 156/x (giờ)
Vận tốc của ô tô lúc về là: x + 32 (km) .
Quãng đường về là: 156 - 36 = 120 km.
Vậy vận tốc của ô tô lúc đi từ A đến B là 48km/h
*Phương pháp giải:
Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.
Bước 2: Biểu diễn các đại lượng chưa biết qua ẩn và đại lượng đã biết.
Bước 3: Lập phương trình và giải phương trình.
Bước 4: Kiểm tra điều kiện và kết luận.
*Lý thuyết:
Bước 1: Lập phương trình
- Chọn ẩn số và đặt điều kiện thích hợp cho ẩn số.
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
- Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải hệ phương trình
Bước 3: Trả lời
Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thoả mãn điều kiện của ẩn, nghiệm nào không, rồi kết luận.
2. Lưu ý về chọn ẩn và điều kiện thích hợp của ẩn
- Thông thường thì bài toán hỏi về đại lượng gì thì chọn ẩn là đại lượng đó.
- Về điều kiện thích hợp của ẩn
+ Nếu x biểu thị một chữ số thì , .
+ Nếu x biểu thị tuổi, sản phẩm, người thì x nguyên dương.
+ Nếu x biểu thị vận tốc của chuyển động thì x > 0.
Xem thêm
Lý thuyết Giải bài toán bằng cách lập hệ phương trình (mới 2024 + Bài Tập) – Toán 9
Câu 9:
18/07/2024Để phục vụ cho Festival Huế 2018, một cơ sở sản xuất nón lá dự kiến làm ra 300 chiếc nón lá trong một thời gian đã định. Do được bổ sung thêm nhân công nên mỗi ngày cơ sở đó làm ra được nhiều hơn 5 chiếc nón lá so với dự kiến ban đầu, vì vậy cơ sở sản xuất đã hoàn thành 300 chiếc nón lá sớm hơn 3 ngày so với thời gian đã định. Hỏi theo dự kiến ban đầu, mỗi ngày cơ sở đó làm được ra bao nhiêu chiếc nón lá? Biết rằng số chiếc nón lá làm ra mỗi ngày là bằng nhau và nguyên chiếc.
Xem đáp án
Đáp án C
Gọi số chiếc nón lá mỗi ngày cơ sở đó làm được theo dự kiến là x (chiếc)
Số ngày cơ sở đó dự kiến làm hết 300 chiếc nón lá là: 300/x (ngày)
Sau khi làm tăng thêm 5 chiếc nón lá một ngày thì thời gian cơ sở đó làm hết 300 chiếc nón lá là: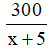 
(ngày).
Theo đề bài ta có phương trình:
Vậy theo dự kiến, mỗi ngày cơ sở đó làm được 20 chiếc nón lá.
Câu 10:
23/07/2024Một ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút. Tính vận tốc thực của ca nô biết quãng đường sông AB dài 54 km và vận tốc dòng nước là 3 km/h.
Xem đáp án
Đáp án A
Đổi 7 giờ 30 phút= 15/2 (h)
Gọi vận tốc thực của ca nô là x (km/h; x > 3).
vận tốc của ca nô khi xuôi dòng sông từ A đến B là: x + 3 (km/h)
Vận tốc của ca nô khi ngược dòng sông từ B về A là: x – 3 (km/h)
Thời gian của ca nô khi xuôi dòng sông từ A đến B là: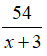 
(h)
Thời gian của ca nô khi ngược dòng sông từ B về A là: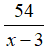 
(h)
Do ca nô chạy xuôi dòng sông từ A đến B rồi chạy ngược dòng từ B về A hết tất cả 7 giờ 30 phút nên ta có phương trình:
Ta thấy chỉ có x = 15 thỏa mãn điều kiện x > 3.
Vậy vận tốc thực của ca nô là 15 (km/h).