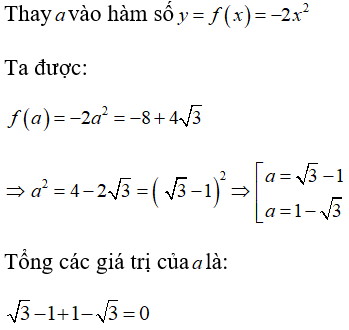Trắc nghiệm Toán 9 Bài 1 (có đáp án): Hàm số y = ax^2 (a khác 0)
-
573 lượt thi
-
22 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
19/07/2024Cho hàm số y = ax2 với . Kết luận nào sau đây là đúng:
 Xem đáp án
Xem đáp án
Đáp án C
Cho hàm số y
• Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
• Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0
Câu 2:
13/07/2024Kết luận nào sau đây sai khi nói về đồ thị hàm số y = a với a 0
 Xem đáp án
Xem đáp án
Đáp án B
Đồ thị hàm số là một parabol đi qua gốc tọa độ O, nhận Oy làm trục đối xứng (O là đỉnh của parabol).
• Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhất của đồ thị
• Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhất của đồ thị
Câu 3:
08/07/2024Giá trị của hàm số y = f(x) = -7 tại = -2 là:
 Xem đáp án
Xem đáp án
Đáp án D
Thay vào hàm số y = f(x) = -7 ta được: f(-2) = -7. = -28
Câu 4:
22/07/2024Cho hàm số y = f(x) = (-2m + 1) . Tính giá trị của m để đồ thị đi qua điểm A(-2; 4)
 Xem đáp án
Xem đáp án
Đáp án A
Thay tọa độ điểm A(-2; 4) vào hàm số y = f(x) = (-2m + 1) ta được:
(-2m + 1). = 4 ⇔ -2m + 1 = 1 ⇔ m = 0
Vậy m = 0 là giá trị cần tìm.
Câu 5:
17/07/2024Cho hàm số y = f(x) = -2. Tổng các giá trị a của thỏa mãn f(a) = là:
 Xem đáp án
Xem đáp án
Đáp án B
Câu 6:
23/07/2024Cho hàm số y = (m + 1) + 2. Tìm m biết rằng với x = 1 thì y = 5.
 Xem đáp án
Xem đáp án
Đáp án A
Thay x = 1 và y = 5 vào ta được:
5 = (m +1).1 + 2
⇔ m + 1 + 2 = 5 ⇔ m = 2
Câu 7:
22/07/2024Cho hàm số y= 2 . Tìm x khi y = 32 ?
 Xem đáp án
Xem đáp án
Đáp án D
Thay y = 32 vào y = 2 ta được:
⇔ x = ±4
Câu 8:
23/07/2024Diện tích hình tròn bán kính R được cho bởi công thức: S = π..
Hỏi nếu bán kính tăng lên 6 lần thì diện tích tăng hay giảm bao nhiêu lần?
 Xem đáp án
Xem đáp án
Đáp án C
Diện tích hình tròn ban đầu là: S =
Khi tăng bán kính lên 6 lần thì bán kính mới là R’ = 6R.
Diện tích hình tròn mới là: S =
Do đó, diện tích hình tròn mới tăng lên 36 lần.
Câu 9:
15/07/2024Cho các hàm số y = 2 và y = . Hỏi hàm số nào đồng biến khi x > 0
 Xem đáp án
Xem đáp án
Đáp án A
Xét hàm số y = ax2 (a ≠ 0)
* Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
* Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Do đó,chỉ có hàm số y = 2x2 đồng biến khi x> 0.
Câu 10:
21/07/2024Cho các hàm số:
(1): y = 3
(2): y = - 4
(3) y = 3x
(4): y = - 4x .
Hỏi có bao nhiều hàm số đồng biến với x < 0?
 Xem đáp án
Xem đáp án
Đáp án B
* Hàm số bậc nhất y = ax + b đồng biến khi a > 0 và hàm số này nghịch biến khi a < 0 .
Do đó, hàm số y = 3x đồng biến trên R nên cũng đồng biến khi x < 0 .
Hàm số y = -4x nghịch biến trên R.
* Xét hàm số y = ax2 (a ≠ 0)
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Trong hai hàm số y = 3x2 và y = -4x2 chỉ có hàm số y = -4x2 đồng biến khi x < 0
Vậy trong các hàm số đã cho chỉ có hàm số y = 3x và y = -4x2 đồng biến x < 0.
Câu 11:
23/07/2024Cho parabol (P): và đường thẳng (d): y = 5x + 4. Tìm m để đường thẳng d cắt (P) tại điểm có tung độ y = 9
 Xem đáp án
Xem đáp án
ĐK:
Thay y = 9 vào phương trình đường thẳng d ta được 9 = 5x + 4x = 1
nên tọa độ giao điểm của đường thẳng d và parabol (P) là (1; 9)
Thay x = 1; y = 9 vào hàm số y =.x2 ta được
5m + 1 = 815m = 80m = 16 (TM)
Vậy m = 16 là giá trị cần tìm
Đáp án cần chọn là: D
Câu 12:
22/07/2024Cho parabol (P):và đường thẳng (d): y = 2x + 2. Biết đường thẳng d cắt (P) tại một điểm có tung độ y = 4. Tìm hoành độ giao điểm còn lại của d và parabol (P)
 Xem đáp án
Xem đáp án
Thay y = 4 vào phương trình đường thẳng d ta được 2x + 2 = 4x = 1
Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (1; 4)
Thay x = 1; y = 4 vào hàm số ta được:
1 – 2m = 8
Khi đó (P): y = 4
Xét phương trình hoành độ giao điểm của d và (P):
4x2 = 2x + 22x2 – x – 1 = 0
(2x + 1) (x – 1) = 0
Vậy hoành độ giao điểm còn lại là
Đáp án cần chọn là: A
Câu 13:
07/07/2024Cho parabol (P): và đường thẳng (d): y = 3x – 5. Biết đường thẳng d cắt (P) tại một điểm có tung độ y = 1. Tìm m và hoành độ giao điểm còn lại của d và parabol (P)
 Xem đáp án
Xem đáp án
ĐKXĐ: m
Thay y = 1 vào phương trình đường thẳng d ta được 3x – 5 = 1x = 2
Nên tọa độ giao điểm của đường thẳng d và parabol (P) là (2; 1)
Thay x = 2; y = 1 vào hàm số x22
ta được:
3m + 4 = 4
3m = 0m = 0 (tm)(P):
Xét phương trình hoành độ giao điểm của d và (P):
x2 – 12x + 20 = 0
(x – 2) (x – 10) = 0
Vậy hoành độ giao điểm còn lại là x = 10
Đáp án cần chọn là: D
Câu 14:
21/07/2024Cho đồ thị hàm số (P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình có hai nghiệm phân biệt.
 Xem đáp án
Xem đáp án
Ta có 2x2 – m – 5 = 0 (*)
2x2 = m + 5
Số nghiệm của phương trình (*) là số giao điểm của
parabol (P): y = 2x2và đường thẳng d: y = m + 5
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại
hai điểm phân biệt.Từ đồ thị hàm số ta thấy:
Với m + 5 > 0m > −5 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > −5
Đáp án cần chọn là: D
Câu 15:
21/07/2024Cho đồ thị hàm số(P) như hình vẽ. Dựa vào đồ thị, tìm m để phương trình có hai nghiệm phân biệt
 Xem đáp án
Xem đáp án
Xét phương trình x2 – 2m + 4 = 0 (*)
x2 = 2m – 4
Số nghiệm của phương trình (*) là
số giao điểm của parabol (P):
và đường thẳng d: y = m – 2
Để (*) có hai nghiệm phân biệt thì d cắt (P) tại hai điểm phân biệt
Từ đồ thị hàm số ta thấy:
Với m – 2 > 0m > 2 thì d cắt (P)
tại hai điểm phân biệt hay phương trình (*)
có hai nghiệm phân biệt khi m > 2
Đáp án cần chọn là: A
Câu 16:
12/07/2024Trong các điểm: A (1; 2); B (−1; −1); C (10; −200); D có bao nhiêu điểm thuộc đồ thị hàm số (P) 222222222222222222222222222222sdvvfbzdfbdsscx2sdsgvd
 Xem đáp án
Xem đáp án
Thay tọa độ điểm A (1; 2) vào hàm số y = −x2
ta được 2 = −12 (vô lý) nên A (P)
Thay tọa độ điểm C (10; −200) vào hàm số y = −x2
ta được – 200 = − (10)2
−200 = −100 (vô lý) nên C (P)
Thay tọa độ điểm D vào hàm số y = −x2
ta được −10 = −10 = −10 (luôn đúng) nên D(P)
Thay tọa độ điểm B (−1; −1) vào hàm số y = −x2
ta được −1 = − (−1)2
−1 = −1 (luôn đúng) nên B (P)
Vậy có hai điểm thỏa mãn.
Đáp án cần chọn là: D
Câu 17:
21/07/2024Trong các điểm A (5; 5); B (−5; −5); C (10; 20); D ( ; 2) có bao nhiêu điểm không thuộc đồ thị hàm số (P)
 Xem đáp án
Xem đáp án
Thay tọa độ điểm A (5; 5) vào hàm số
ta được (luôn đúng) nên A (P)
+) Thay tọa độ điểm B (−5; −5) vào hàm số
ta được −5 = 5 (vô lý) nên B (P)
+) Thay tọa độ điểm D ( ; 2) vào hàm số
ta được 2 = 2 (luôn đúng) nên D (P)
+) Thay tọa độ điểm C (10; 20) vào hàm số
ta được 20 = 20 (luôn đúng) nên C (P)
Vậy có 1 điểm không thuộc (P): là điểm B (−5; −5)
Đáp án cần chọn là: A
Câu 18:
21/07/2024Cho (P): ; (d): y = . Tìm tọa độ giao điểm của (P) và (d)
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d
x2 – 2x + 1 = 0
(x – 1)2 = 0x − 1 = 0x = 1
Thay x = 1 vào hàm số
ta được
Nên tọa độ giao điểm cần tìm là
Đáp án cần chọn là: A
Câu 19:
20/07/2024Cho parabol. Xác định m để điểm A (; m) nằm trên parabol
 Xem đáp án
Xem đáp án
Thay x = ; y = m vào hàm số
ta được
Vậy
Đáp án cần chọn là: A
Câu 20:
20/07/2024Cho parabol (P). Xác định m để điểm A (m; −2) nằm trên parabol
 Xem đáp án
Xem đáp án
Thay x = m ; y = −2 vào hàm số ta được
Vậy
Đáp án cần chọn là: D
Câu 21:
20/07/2024Cho parabol (P): và đường thẳng (d): y = x + 1. Số giao điểm của đường thẳng d và parabol (P) là
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d
2x2 = x + 12x2 – x – 1 = 02x2 – 2x + x – 1 = 0
2x(x – 1) + (x− 1) = 0
(2x + 1) (x – 1) = 0
Vậy có hai giao điểm của đường thẳng d và parabol (P)
Đáp án cần chọn là: D
Câu 22:
20/07/2024Cho parabol (P): và đường thẳng (d): y = −4x – 4. Số giao điểm của đường thẳng d và parabol (P) là:
 Xem đáp án
Xem đáp án
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d
5x2 = −4x – 45x2 + 4x + 4 = 0
4x2 + x2 + 4x + 4 = 0
x2 + (x + 2)2 = 0(*)
Xét x2 + (x + 2)2 0; x và dấu “=” xảy ra khi
(vô lý)
nên x2 + (x + 2)2> 0, x
Hay phương trình (*) vô nghiệm
Vậy không có giao điểm của đường thẳng (d) và parabol (P)
Đáp án cần chọn là: B
Bài thi liên quan
-
Trắc nghiệm Toán 9 Bài 1 (có đáp án): Hàm số y = ax^2 (a ≠ 0) (phần 2)
-
24 câu hỏi
-
50 phút
-
Có thể bạn quan tâm
- Toán 9: Bài 1: Hàm số y = ax2 (a ≠ 0) (572 lượt thi)
Các bài thi hot trong chương
- Toán 9: Bài 6: Hệ thức Vi-ét và ứng dụng (1389 lượt thi)
- Toán 9: Bài 5: Công thức nghiệm thu gọn (1336 lượt thi)
- Toán 9: Bài 8: Giải bài toán bằng cách lập phương trình (1311 lượt thi)
- Toán 9: Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0) (1188 lượt thi)
- Ôn tập chương 4 (1074 lượt thi)
- Toán 9: Bài 4: Công thức nghiệm của phương trình bậc hai (952 lượt thi)
- Toán 9: Bài 7: Phương trình quy về phương trình bậc hai (497 lượt thi)
- Toán 9: Bài 3: Phương trình bậc hai một ẩn (365 lượt thi)