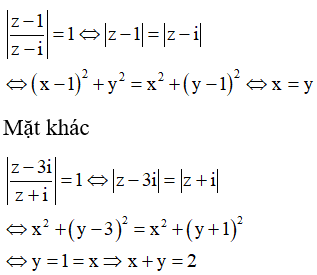30 câu hỏi trắc nghiệm thuộc Bài tập số phức mức độ cơ bản, nâng cao cực hay có lời giải chi tiết(P1) (Đề 1)

Cho hai số phức $z_{1} = - 1 + 2 i, z_{2} = - 1 - 2 i$ . Giá trị của biểu thức ${|z_{1}|}^{2} + {|z_{2}|}^{2}$ bằng

A. $\sqrt{10}$

B. 10

C. -6

D. 4

Xem đáp án

Đáp án B

$z_{1} = - 1 + 2 i \Rightarrow |z_{1}| = \sqrt{{(- 1)}^{2} + 2^{2}} = \sqrt{5} z_{2} = - 1 - 2 i \Rightarrow |z_{2}| = \sqrt{{(- 1)}^{2} + {(- 2)}^{2}} = \sqrt{5} \Rightarrow {|z_{1}|}^{2} + {|z_{2}|}^{2} = 5 + 5 = 10$

Câu 3:

17/07/2024

Biết phương trình $z^{2} + a z + b = 0 (a, b \in ℝ)$ có một nghiệm là z = -2 + i. Tính a + b

A. 9.

B. 1.

C. 4

D. -1

Xem đáp án

Đáp án A

$Ta dễ dàng suy ra nghiệm còn lại của phương trình là z_{2} = - 2 - i Áp dụng hệ thức Vi - ét : \{\begin{cases} z_{1} + z_{2} = - 2 + i - 2 - i = - a \Rightarrow a = 4 \\ z_{1} z_{2} = (- 2 + i) (- 2 - i) = {(- 2)}^{2} - i^{2} = 4 + 1 = 5 = b \end{cases} \Rightarrow a + b = 4 + 5 = 9$

Câu 4:

Cho số phức z thỏa mãn phương trình 4|z+i| + 3|z-i| = 10. Tính giá trị nhỏ nhất của |z|

A. $\frac{1}{2}$

B. $\frac{5}{7}$

C. $\frac{3}{2}$

D. 1

Xem đáp án

Đáp án D

$Đặt z = a + bi (a; b \in ℝ) Ta có : |z + i| = \sqrt{a^{2} + {(b + 1)}^{2}} = \sqrt{a^{2} + b^{2} + 2 b + 1} = \sqrt{{|z|}^{2} + 2 b + 1} Tương tự : |z - i| = \sqrt{{|z|}^{2} - 2 b + 1} Áp dụng BĐT bunhiacopski dạng (a^{2} + b^{2}) (c^{2} + d^{2}) \leq {(ac + bd)}^{2} \Rightarrow 4 |z + i| + 3 |z - i| \leq \sqrt{4^{2} + 3^{2}} . \sqrt{{|z + i|}^{2} + {|z - i|}^{2}} \Leftrightarrow 10 \leq 5 \sqrt{{|z|}^{2} + 2 b + 1 + {|z|}^{2} - 2 b + 1} = 5 \sqrt{2 {|z|}^{2} + 2} \Leftrightarrow 4 \leq 2 {|z|}^{2} + 2 \Leftrightarrow {|z|}^{2} \geq 1 \Leftrightarrow |z| \geq 1 KL : {|z|}_{\min} = 1$

Câu 5:

16/07/2024

Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức z = (1+i)(2-i)?

A. P

B. M

C. N

D. Q

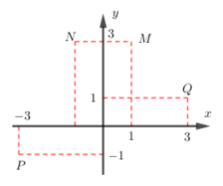
Xem đáp án

Đáp án D

$z = (1 + i) (2 - i) = 2 - i + 2 i - i^{2} = 2 + i + 1 = 3 + i \Rightarrow Điểm biểu diễn số phức z là Q (3; 1)$

Câu 6:

Tập hợp tất cả các điểm biểu diễn các số phức z thỏa mãn | $\bar{z}$ +2-i| = 4 là đường tròn có tâm I và bán kính R lần lượt là

A. I(-2;-1), R = 4

B. I(-2;-1), R = 2

C. I(2;-1), R = 4

D. I(2;-1), R = 2

Xem đáp án

Đáp án A

$Gọi z = a + bi (a; b \in ℝ) \Rightarrow \bar{z} = a - bi \Rightarrow |\bar{z} + 2 - i| = |a + 2 - (b + 1) i| = \sqrt{{(a + 2)}^{2} + {(b + 1)}^{2}} = 4 \Rightarrow {(a + 2)}^{2} + {(b + 1)}^{2} = 16 KL : Tập hợp tất cả các điểm biểu diễn số phức z thỏa mãn đề bài nằm trên đường tròn tâm I (- 2; - 1), bán kính R = 4$

Câu 7:

Cho số phức z = x + yi (a,b $\in ℝ$ ) thỏa mãn $|\frac{z - 1}{z - i}| = 1 và |\frac{z - 3 i}{z + i}| = 1$ . Tính P = x + y.

A. P = 7

B. P = -1

C. P = 1

D. P = 2

Xem đáp án

Đáp án D

Câu 8:

Điểm M trong hình vẽ là biểu diễn hình học của số phức nào dưới đây?

A. z = 2 - i

B. z = 2 + i

C. z = -1 + 2i

D. z = -1 - 2i

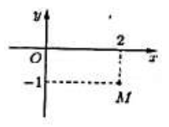
Xem đáp án

Đáp án A

Điểm M(2;-1) biểu diễn số phức z = 2-i

Câu 9:

16/07/2024

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z-1+i| = 2 là đường tròn có tâm và bán kính lần lượt là

A. I(-1;1), R = 4

B. I(-1;1), R = 2

C. I(1;-1), R = 2

D. I(1;-1), R = 4

Xem đáp án

Đáp án C

Gọi z = x+yi (x;y $\in ℝ$ )

$\Rightarrow |z - 1 + i| = |x - 1 + (y + 1) i| = \sqrt{{(x - 1)}^{2} + {(y + 1)}^{2}} = 2 \Rightarrow {(x - 1)}^{2} + {(y + 1)}^{2} = 4 KL : Tập hợp các điểm biểu diễn số phức z thỏa mãn yêu cầu bài toán năm trên đường tròn tâm I (1; - 1) có bán kính R = 2 Tổng quát : Nếu số phức z thỏa mãn |z - a + bi| = c thì tập hợp các điểm thỏa mãn nằm trên đường tròn tâm I (a; - b) có bán kính R = c$

Câu 10:

Gọi $z_{1} v à z_{2}$ là hai nghiệm phức của phương trình $z^{2}$ + 2z + 10 = 0. Giá trị của $|z_{1}^{2}| + |z_{2}^{2}|$ bằng

A. $\sqrt{10}$

B. 20

C. 2 $\sqrt{10}$

D. 10

Xem đáp án

Đáp án B

$Giải PT : z^{2} + 2 z + 10 = 0 \Leftrightarrow \{\begin{cases} z_{1} = - 1 + 3 i \\ z_{2} = - 1 - 3 i \end{cases} \Rightarrow |z_{1}^{2}| = |{(- 1 + 3 i)}^{2}| = |1 - 6 i + 9 i^{2}| = |- 8 - 6 i| = 10 tương tự : |z_{2}^{2}| = |{(- 1 - 3 i)}^{2}| = |1 + 6 i + 9 i^{2}| = |- 8 + 6 i| = 10 \Rightarrow |z_{1}^{2}| + |z_{2}^{2}| = 10 + 10 = 20$

Câu 11:

15/07/2024

Cho hai số thực x,y thỏa mãn x(3+2i) + y(1-4i) = 11+12i. Giá trị của x + y bằng

A. 3.

B. -7.

C. –3.

D. 7.

Xem đáp án

Đáp án A

$Ta có : x (3 + 2 i) + y (1 - 4 i) = 3 x + y + (2 x - 4 y) i = 11 + 12 i \Rightarrow \{\begin{array}{l} 3 x + y = 11 \\ 2 x - 4 y = 12 \end{array} \Leftrightarrow \{\begin{cases} x = 4 \\ y = - 1 \end{cases} \Rightarrow x + y = 4 - 1 = 3$

Câu 12:

Tìm hai số thực x và y thỏa mãn (2x-3yi) + (1-3i) = x + 6i với i là đơn vị ảo.

A. x = -1; y = -3

B. x = -1; y = -1

C. x = 1; y = -1

D. x = 1; y = -3

Xem đáp án

Đáp án A

$(2 x - 3 yi) + 1 - 3 i = 2 x + 1 - (3 y + 3) i = x + 6 i \Rightarrow \{\begin{array}{l} 2 x + 1 = x \\ 3 y + 3 = - 6 \end{array} \Leftrightarrow \{\begin{cases} x = - 1 \\ y = - 3 \end{cases}$

Câu 13:

Lý thuyết Số phức hay, chi tiết

Xét các số phức z thỏa mãn ( $\bar{z}$ +i)(z+2) là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn các số phức z là một đường tròn có bán kính bằng

A. 1

B. $\frac{5}{4}$

C. $\frac{\sqrt{5}}{2}$

D. $\frac{\sqrt{3}}{2}$

Xem đáp án

Đáp án C

$Gọi z = a + bi (a; b \in ℝ) \Rightarrow \bar{z} = a - bi \Rightarrow (\bar{z} + i) (z + 2) = (a - bi + i) (a + bi + 2) = [a + (1 - b) i] [a + 2 + bi] = a (a + 2) + abi + (a + 2) (1 - b) i + b (1 - b) i^{2} = a^{2} + 2 a - b (1 - b) + [ab + (a + 2) (1 - b)] i = a^{2} + 2 a + b^{2} - b + (a + 2 - 2 b) i (*) Để (*) là số thuần ảo thì a^{2} + 2 a + b^{2} - b = 0 \Leftrightarrow {(a + 1)}^{2} + {(b - \frac{1}{2})}^{2} - \frac{1}{4} - 1 = 0 \Leftrightarrow {(a + 1)}^{2} + {(b - \frac{1}{2})}^{2} = \frac{5}{4} \Rightarrow Tập hợp các điểm biểu diễn các số phức z là đường tròn tâm I (- 1; \frac{1}{2}), bán kính R = \frac{\sqrt{5}}{2}$

Câu 14:

10/12/2024

Có bao nhiêu số phức z thỏa mãn |z|(z-4-i) + 2i = (5-i)z?

A. 2

B. 3

C. 1

D. 4

Xem đáp án

Đáp án đúng là B

Lời giải

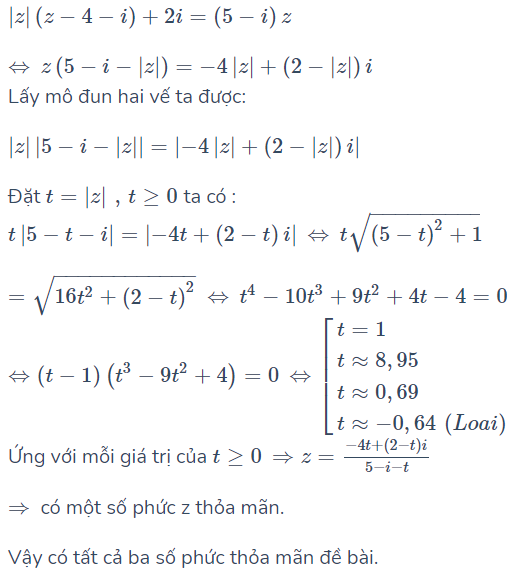
*Phương pháp giải:

Áp dụng phương pháp modul 2 vế

*Lý thuyết:

1. Số i.

Số i là số thỏa mãn: i² = –1.

2. Định nghĩa số phức

Mỗi biểu thức dạng a + bi , trong đó $a; b \in R$ ; i² = –1 được gọi là một số phức.

Đối với số phức z = a + bi, ta nói: a là phần thực, b là phần ảo của z.

Tập hợp các số phức kí hiệu là C.

Ví dụ 1. Các số sau là những số phức: 2 – 3i; –8 + 4i; $5 - i \sqrt{2};$ $\sqrt{3} + 2 i$

Ví dụ 2. Số phức 6 – i có phần thực là 6, phần ảo là – 1.

3. Số phức bằng nhau

– Định nghĩa : Hai số phức bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau :

a + bi = c + di a = c và b = d.

– Chú ý :

a) Mỗi số thực a được coi là một số phức với phần ảo bằng 0: a = a + 0i.

Như vậy, mỗi số thực cũng là một số phức. Ta có : $R \subset C$ .

b) Số phức 0 + bi được gọi là số thuần ảo và viết đơn giản là bi : bi = 0 + bi

Đặc biệt : i = 0 + 1.i

Số i được gọi là đơn vị ảo.

Xem thêm

TOP 40 câu Trắc nghiệm Số phức (có đáp án 2024) - Toán 12

Câu 15:

Số phức -3 + 7i có phần ảo bằng

A. 3.

B. -7.

C. –3.

D. 7.

Xem đáp án

Đáp án D

Số phức z = a+bi có phần thực là a, phần ảo là b nên

Số phức z = -3+7i có phần ảo là 7

Câu 16:

Phần ảo của số phức z = 5 + 2i bằng:

A. 5

B. 5i

C. 2

D. 2i

Xem đáp án

Đáp án C

Số phức z = a+bi có phần thực là a, phần ảo là b nên

Số phức z = 5+2i có phần ảo là 2

Câu 17:

Tập hợp các điểm biểu diễn số phức z thỏa mãn |z+2| = |z-i| là một đường thẳng có phương trình

A. 4x + 2y + 3 = 0

B. 2x + 4y + 13 = 0

C. 2x - 4y + 13 = 0

D. $\{\begin{cases} x = 4 + t \\ y = - 2 + t \\ z = 1 + t \end{cases}$

Xem đáp án

Đáp án A

$Đặt z = a + bi (a; b \in ℝ) |z + 2| = |z - i| \Leftrightarrow |a + 2 + bi| = |a + (b - 1) i| \Leftrightarrow {(a + 2)}^{2} + b^{2} = a^{2} + {(b - 1)}^{2} \Leftrightarrow 4 a + 4 = - 2 b + 1 \Leftrightarrow 4 a + 2 b + 3 = 0 KL : Tập hợp các điểm biểu diễn số phức z thoả mãn yêu cầu đề bài nằm trên đường thẳng 4 x + 2 y + 3 = 0$

Câu 18:

Cho z là số phức thỏa mãn | $\bar{z}$ | = |z+2i|. Giá trị nhỏ nhất của |z-1+2i| + |z+1+3i| là

$A . \sqrt{5}$

$B . 5 \sqrt{2}$

$C . \sqrt{13}$

$D . \sqrt{29}$

Xem đáp án

Đáp án C

Câu 19:

Cho số phức z = 6 + 7i. Số phức liên hợp của z là

A. $\bar{z}$ = 6 + 7i

B. $\bar{z}$ = -6 + 7i

C. $\bar{z}$ = -6 - 7i

D. $\bar{z}$ = 6 - 7i

Xem đáp án

Đáp án D

Số phức z = 6+7i có số phức liên hợp là $\bar{z} = 6 - 7 i$

Câu 20:

Tính mô đun của số phức z, biết (1-2i)z + 2 - i = -12i

A. 5

B. $\sqrt{7}$

C. $\frac{1}{5}$

D. $2 \sqrt{2}$

Xem đáp án

Đáp án A

$(1 - 2 i) z + 2 - i = - 12 i \Leftrightarrow (1 - 2 i) z = - 2 - 11 i \Leftrightarrow z = \frac{- 2 - 11 i}{1 - 2 i} = \frac{(- 2 - 11 i) (1 + 2 i)}{1^{2} - 4 i^{2}} = \frac{20 - 15 i}{5} = 4 - 3 i \Rightarrow |z| = \sqrt{4^{2} + {(- 3)}^{2}} = 5$

Câu 21:

Cho số phức z thỏa mãn $3 |z + \bar{z}| + 2 |z - \bar{z}| \leq 12$ . Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của |z-4+3i|. Giá trị M.m bằng

A. 20

B. 24

C. 26

D. 28

Xem đáp án

Đáp án B

Câu 22:

Tập hợp các điểm M biểu diễn số phức z sao cho $z^{2} = {(\bar{z})}^{2}$ là

A. Trục tung và trục hoành.

B. Trục tung.

C. Trục hoành.

D. Gốc tọa độ.

Xem đáp án

Đáp án A

$Đặt z = x + yi (x; y \in ℝ) \Rightarrow \bar{z} = x - yi Theo đề bài : z^{2} = {(\bar{z})}^{2} \Leftrightarrow {(x + yi)}^{2} = {(x - yi)}^{2} \Leftrightarrow x^{2} + 2 xyi - y^{2} = x^{2} - 2 xyi - y^{2} \Leftrightarrow 4 xyi = 0 \Leftrightarrow x = 0 hoặc y = 0 KL : Tập hợp các điểm M biểu diễn số phức z thỏa mãn yêu cầu bài toán nằm trên trục hoành hoặc nằm trên trục tung$

Câu 23:

Gọi $z_{1}; z_{2}$ là hai nghiệm phức của phương trình $z^{2} - 4 z + 5 = 0$ . Khi đó phần thực của $z_{1}^{2} + z_{2}^{2}$ là

A. 7.

B. 5.

C. 4.

D. 6.

Xem đáp án

Đáp án D

Giải PT:

$z^{2} - 4 z + 5 = 0 \Leftrightarrow \{\begin{cases} z_{1} = 2 + i \\ z_{2} = 2 - i \end{cases} \Rightarrow z_{1}^{2} + z_{2}^{2} = {(2 + i)}^{2} + {(2 - i)}^{2} = 6$

Câu 24:

Cho hai số phức z, w thỏa mãn $\{\begin{cases} | z - 3 - 2 i | \leq 1 \\ | w + 1 + 2 i | \leq | w - 2 - i | \end{cases}$ . Tìm gía trị nhỏ nhất $P_{m i n}$ của biểu thức P = |z-w|.

$A . P_{m i n} = \frac{3 \sqrt{2} - 2}{2}$

$B . P_{m i n} = \sqrt{2} + 1$

$C . P_{m i n} = \frac{5 \sqrt{2} - 2}{2}$

$D . P_{m i n} = \frac{2 \sqrt{2} + 1}{2}$

Xem đáp án

Đáp án C

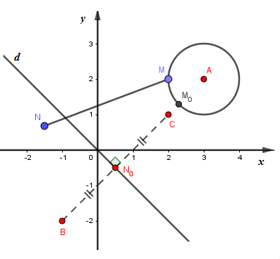
Đặt $A (3; 2), B (- 1; - 2), C (2; 1)$ . Gọi M, N lần lượt là điểm biểu diến của z, w.

Vì $| z - 3 - 2 i | \leq 1$ nên tập hợp điểm biểu diễn của z trên hệ trục Oxy là hình tròn tâm A bán kính 1.

Vì $| w + 1 + 2 i | \leq | w - 2 - i |$ nên tập hợp điểm biểu diễn của w trên hệ trục Oxy là nửa mặt phẳng bờ d chứa B và đường thẳng d. Trong đó d là trung trực của đoạn thẳng BC.

$P = | z - w | = M N$ , $P_{\min} = {MN}_{\min}$

Dễ dàng kiểm tra được A, B, C thẳng hàng và MN ngắn nhất khi MN trùng với $M_{0} N_{0}$

Trong đó, $N_{0}$ : trung điểm của BC, $M_{0}$ : giao của AB và đường tròn $(A; 1)$

Độ dài đoạn $M_{0} N_{0} = d (A; d) - R = d (A; d) - 1$

Phương trình đường thẳng d có:

$N_{0}$ là trung điểm BC $\Rightarrow N_{0} (\frac{1}{2}; \frac{- 1}{2})$

$\vec{B C} = (3; 3) \Rightarrow d$ $d có 1 VTPT là (1; 1)$

Phương trình đường thẳng d: $1 (x - \frac{1}{2}) + 1 (y - \frac{- 1}{2}) = 0 \Leftrightarrow x + y = 0$

$d (A; d) = \frac{| 3 + 2 |}{\sqrt{1^{2} + 1^{2}}} = \frac{5}{\sqrt{2}} \Rightarrow M_{o} N_{0} = \frac{5}{\sqrt{2}} - 1 = \frac{5 \sqrt{2} - 2}{2}$

Vậy, $P_{min} = \frac{5 \sqrt{2} - 2}{2}$

Câu 25:

Cho các góc $α, β$ và có số phức z = cos $α$ + i.sin $β$ . Khi đó x = z.w thì:

$A . x = \cos (α - β) + i . \sin (α + β)$

$B . x = \cos (α + β) + i . \sin (α + β)$

$C . x = \cos (α β) + i . \sin (α β)$

$D . x = \sin (α - β) + i . \cos (α + β)$

Xem đáp án

Đáp án B

Câu 26:

15/07/2024

Biết các số phức z,w khác 0 thỏa mãn: $z^{2} + w^{2}$ = zw Khi đó:

$A . z^{6} = w^{6}$

$B . z^{5} = w^{5}$

$C . z^{4} = i w^{4}$

$D . z^{3} + i w^{3} = 0$

Xem đáp án

Đáp án A

Câu 27:

15/07/2024

Biết số phức z thỏa mãn: $\frac{z + 1}{z - 1}$ là số thuần ảo. Khi đó ta phải có:

$A . i z \notin ℝ$

$B . | z | = 4$

$C . | z | = 1$

$D . z = \frac{1}{2} - i . \frac{\sqrt{3}}{2}$

Xem đáp án

Đáp án C

$Đặt z = a + bi (a; b \in ℝ) \Rightarrow \frac{z + 1}{z - 1} = 1 + \frac{2}{z - 1} = 1 + \frac{2}{a - 1 + bi} = 1 + \frac{2 (a - 1 - bi)}{{(a - 1)}^{2} + b^{2}} = 1 + \frac{2 (a - 1)}{{(a - 1)}^{2} + b^{2}} - \frac{2 b}{{(a - 1)}^{2} + b^{2}} i Để \frac{z + 1}{z - 1} là số thuần ảo thì \{\begin{cases} 1 + \frac{2 (a - 1)}{{(a - 1)}^{2} + b^{2}} = 0 \\ \frac{- 2 b}{{(a - 1)}^{2} + b^{2}} \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} b \neq 0 \\ {(a - 1)}^{2} + b^{2} + 2 (a - 1) = 0 \end{cases} \Leftrightarrow \{\begin{cases} b \neq 0 \\ a^{2} + b^{2} = 1 \end{cases} \Rightarrow |z| = 1$

Câu 28:

Biết $1 + i + i^{2} + . . . . + i^{100} = a + b i (a, b \in ℝ)$ . Tìm a,b.

$A . \{\begin{cases} a = 0 \\ b = 1 \end{cases}$

$B . \{\begin{cases} a = 1 \\ b = 0 \end{cases}$

$C . \{\begin{cases} a = 1 \\ b = 1 \end{cases}$

$D . \{\begin{cases} a = - 1 \\ b = - 1 \end{cases}$

Xem đáp án

Đáp án B

$Ta có i^{2 k} + i^{2 k + 2} = i^{2 k} (1 + i^{2}) = 0 và i^{2 k + 1} + i^{2 k + 3} = i^{2 k + 1} (1 + i^{2}) = 0 \Rightarrow 1 + i + i^{2} + . . . + i^{100} = 1 + (i + i^{3}) + (i^{2} + i^{4}) + . . . + (i^{97} + i^{99}) + (i^{98} + i^{100}) = 1 + 0 + 0 + . . . + 0 + 0 = 1 = a + bi \Rightarrow \{\begin{cases} a = 1 \\ b = 0 \end{cases}$

Câu 29:

Tìm phần thực a của số phức $z = \frac{1 - i . \tan \frac{π}{7}}{1 + i . \tan \frac{π}{7}}$

A. a = 1

B. a = $\sin \frac{2 π}{7}$

C. a = $\tan \frac{π}{7}$

D. a = $\cos \frac{2 π}{7}$

Xem đáp án

Đáp án D

$z = \frac{1 - i . \tan \frac{π}{7}}{1 + i . \tan \frac{π}{7}} = \frac{(1 - i . \tan \frac{π}{7}) (1 - i . \tan \frac{π}{7})}{1 - i^{2} . \tan^{2} \frac{π}{7}} = \frac{1 - \tan^{2} \frac{π}{7} - 2 i . \tan \frac{π}{7}}{1 + \tan^{2} \frac{π}{7}} \Rightarrow Phần thực của số phức z là : a = \frac{1 - \tan^{2} \frac{π}{7}}{1 + \tan^{2} \frac{π}{7}} = \frac{\cos^{2} \frac{π}{7} - \sin^{2} \frac{π}{7}}{\cos^{2} \frac{π}{7} + \sin^{2} \frac{π}{7}} = \cos \frac{2 π}{7}$

Câu 30: