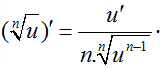30 câu hỏi trắc nghiệm thuộc Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 5)

Câu 1:

17/06/2026

Cho a là số thực dương khác . Mệnh đề nào dưới đây đúng với mọi số dương x, y

Đáp án C

Theo quy tắc tính lôgarit ta có: $\log_{a} (\frac{x}{y}) = \log_{a} x - \log_{a} y$ ( giả sử các biểu thức đều có nghĩa )

Câu 2:

17/06/2026

Giải bất phương trình sau $\log_{\frac{1}{5}} (3 x - 5) > \log_{\frac{1}{5}} (x + 1)$

Xem đáp án

Đáp án A

Câu 3:

17/06/2026

Tập xác định của hàm số y = ln(-x² + 5x - 6) là

Xem đáp án

Đáp án B

Hàm số đã cho xác định

Câu 4:

17/06/2026

Tìm n biết $\frac{1}{\log_{2} x} + \frac{1}{\log_{2^{2}} x} + \frac{1}{\log_{2^{3}} x} + . . . + \frac{1}{\log_{2^{n}} x} = \frac{465}{\log_{2} x}$ luôn đúng với mọi $x > 0, x \neq 1$ .

Xem đáp án

Đáp án C

Ta có

Câu 5:

17/06/2026

Tính tổng S = x₁ + x₂ biết x₁, x₂ là các giá trị thực thỏa mãn đẳng thức $2^{x^{2} - 6 x + 1} = {(\frac{1}{4})}^{x - 3}$ ?

A. S = 4

B. S = 8

C. S = -5

D. S = 2

Xem đáp án

Đáp án A

Phương trình

Câu 6:

17/06/2026

Biết log₆2 = a, log₆5 = b. Tính I = log₃5 theo a, b.

Xem đáp án

Đáp án B

Ta có

Câu 7:

17/06/2026

Trên hình 2.13, đồ thị của ba hàm số y = a^x, y = b^x, y = c^x (a, b, c là ba số dương khác 1 cho trước) được vẽ trong cùng một mặt phẳng tọa độ. Dựa vào đồ thị và các tính chất của lũy thừa, hãy so sánh ba số a, b và c

Xem đáp án

Đáp án C

Dựa vào hình vẽ, ta thấy rằng:

Hàm số y = a^x là hàm số đồng biến; hàm số y = b^x, y = c^x là hàm số nghịch biến.

Suy ra a > 1 và $\{\begin{cases} 0 < b < 1 \\ 0 < c < 1 \end{cases}$ $\to a > \{b; c\}$

Gọi B(-1; y_B) thuộc đồ thị hàm số $y = b^{x} \Rightarrow y_{B} = \frac{1}{b}$

Và C(-1;y_c) thuộc đồ thị hàm số $y = c^{x} \Rightarrow y_{C} = \frac{1}{c}$

Dựa vào đồ thị, ta có $y_{B} > y_{c} \Rightarrow \frac{1}{b} > \frac{1}{c} \Rightarrow c > b$

Câu 8:

17/06/2026

Xét các mệnh đề sau

(1) log₂(x - 1)² + 2log₂(x+1) = 6

<=> 2log₂(x-1) + 2log₂(x+1) = 6

(2) log₂(x²+1) $\geq$ 1 + log₂|x|; $\forall x \in R$

(3) x^lny = y^lnx; $\forall x > y > 2$

$(4) \log_{2}^{2} 2 x - 4 \log_{2} x - 4 = 0 \Leftrightarrow \log_{2}^{2} x - 4 \log_{2} x - 3 = 0$

Số mệnh đề đúng là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Dựa vào giả thiết, ta thấy rằng:

đúng.

=> (4) sai. Vậy có 2 mệnh đề đúng.

Câu 9:

17/06/2026

Giả sử x, y là những số thực dương thỏa mãn: log₁₆(x+y) = log₉x = log₁₂y. Tính giá trị của biểu thức $P = 1 + \frac{x}{y} + {(\frac{x}{y})}^{2}$

Xem đáp án

Đáp án B

Đặt

Câu 10:

17/06/2026

Cho các số thực x, y, z thỏa mãn $3^{x} = 5^{x} = 15^{\frac{2017}{x + y} - z}$ . Gọi S = xy + yz + zx. Khẳng định nào đúng?

Xem đáp án

Đáp án C

Đặt

Đồng thời :

Câu 11:

17/06/2026

Tìm tập hợp các giá trị thực của m sao cho bất phương trình log₂x + m $\geq \frac{1}{2} x^{2}$ có nghiệm $x \in [1; 3]$

Xem đáp án

Đáp án D

Bất phương trình

Xét hàm số

Phương trình

Tính các giá trị

Suy ra giá trị nhỏ nhất của hàm số f(x) là

Khi đó, bất phương trình (*) có nghiệm

Câu 12:

17/06/2026

Cho hai đường cong (C₁): y = 3^x(3^x - m + 2) + m² - 3m và (C₂): y = 3^x + 1. Để (C₁) và (C₂) tiếp xúc nhau thì giá trị của tham số m bằng

Xem đáp án

Đáp án C

Xét đường cong (C₁): f(x) = 3^x(3^x - m + 2) + m² - 3m

Và đường cong (C₂): g(x) = 3^x + 1

Để (C₁) tiếp xúc với (C₂) $\Leftrightarrow \{\begin{cases} f' (x) = g' (x) \\ f (x) = g (x) \end{cases}$

Câu 13:

17/06/2026

Xét các số thực a, b thỏa mãn $a \geq b > 1$ . Biết rằng biểu thức $P = \frac{1}{\log_{a b} a} + \sqrt{\log_{a} \frac{a}{b}}$ đạt giá trị lớn nhất khi b = a^k. Khẳng định nào sau đây đúng?

Xem đáp án

Đáp án D

Dựa vào bảng biến thiên,

Khi đó

Câu 14:

17/06/2026

Biết phương trình $9^{x} - 2^{x + \frac{1}{2}} = 2^{x + \frac{3}{2}} - 3^{2 x - 1}$ có nghiệm là a. Tính giá trị biểu thức $P = a + \frac{1}{2} \log_{\frac{9}{2}} 2$

Xem đáp án

Đáp án B

Câu 15:

17/06/2026

Số nguyên tố dạng M_p = 2^P - 1, trong đó p là một số nguyên tố được gọi là số nguyên tố Mecxen. Số M_6972593 được phát hiện năm 1999. Hỏi rằng nếu viết số đó trong hệ thập phân thì có bao nhiêu chữ số?

A. 2098960 chữ số.

B. 2098961 chữ số

C. 6972593 chữ số

D. 6972592 chữ số

Xem đáp án

Đáp án A

Ta có

Do đó số chữ số của số đó là 2098959 + 1 = 2098960

Câu 16:

17/06/2026

Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?

Xem đáp án

Đáp án đúng: C.

*Lời giải:

Ta có:

+ log (3a) = log 3 + log a nên đáp án A và D sai

+) log a³ = 3loga. nên đáp án C đúng

*Phương pháp giải:

- Áp dụng logarit của một tích: Log_a(b₁. b₂) = log_ab₁ + log_ab₂

_-Áp dụng logarit của một lũy thừa: Log_ab = b loga

* Lý thuyết cần nắm và dạng toán về hàm số logarit và hàm số mũ:

HÀM SỐ LOGARIT:

Định nghĩa logarit

Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.

$α = \log_{a} b \Leftrightarrow a^{α} = b$

– Chú ý: Không có logarit của số âm và số 0.

Tính chất của logarit

Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:

loga1 = 0; logaa = 1

$a^{\log_{a} b} = b; \log_{a} (a^{α}) = α$

Quy tắc tính logarit

Logarit của một tích

– Định lí 1. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:

$\log_{a} (b_{1} . b {}_{2}) = \log_{a} b_{1} + \log_{a} b {}_{2}$

Logarit của một tích bằng tổng các logarit.

– Chú ý:

Định lí 1 có thể mở rộng cho tích n số dương:

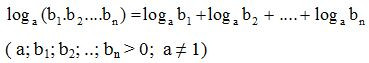
Logarit của một thương

– Định lí 2. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:

$\log_{a} \frac{b_{1}}{b_{2}} = \log_{a} b_{1} - \log_{a} b {}_{2}$

Logarit của một thương bằng hiệu các logarit.

Đặc biệt: $\log_{a} \frac{1}{b} = - \log_{a} b$ ( a > 0; b > 0; a ≠ 1)

Logarit của một lũy thừa

– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:

$\log_{a} b^{α} = α \log_{a} b$

Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.

– Đặc biệt: $\log_{a} \sqrt[n]{b} = \frac{1}{n} \log_{a} b$

Đổi cơ số logarit

– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:

$\log_{a} b = \frac{\log_{c} b}{\log_{c} a}$

– Đặc biệt:

$\begin{array}{l} \log_{a} b = \frac{1}{\log_{b} a} ( b \neq 1) \\ \log_{a^{α}} b = \frac{1}{α} \log_{a} b (α \neq 0) \end{array}$

Logarit thập phân. Logarit tự nhiên

Logarit thập phân

Logarit thập phân là logarit cơ số 10.

log10b thường được viết là logb hoặc lgb.

Logarit tự nhiên

– Logarit tự nhiên là logarit cơ số e. Logeb được viết là lnb.

HÀM SỐ MŨ:

y = a^x, (a > 0, a ≠ 1)

Tập xác định: D = R

Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = a^f(x) thì t > 0

Tính đơn điệu:

+ Khi a > 1 thì hàm số y = a^x đồng biến, khi đó ta luôn có: a^f(x) > a^g(x) ⇔ f(x) > g(x).

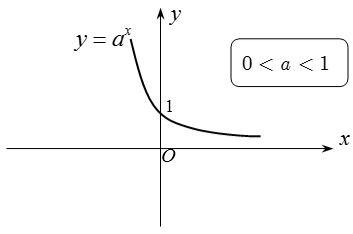
+ Khi 0 < a < 1 thì hàm số y = a^x nghịch biến, khi đó ta luôn có: a^f(x) > a^g(x) ⇔ f(x) < g(x).

Đạo hàm:

(a^x)' = a^x.ln a ⇒ (a^u)' = u'.a^u.ln a

(e^x)' = e^x ⇒ (e^u)' = e^u.u'

Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải

Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.

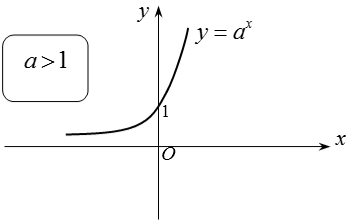
Các dạng bài tập Toán lớp 12 ôn thi THPT Quốc gia có lời giải

Xem thêm các bài viết liên quan hay, chi tiết

Hàm số mũ và hàm số lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải

Toán 12 Bài 4: Hàm số mũ. Hàm số lôgarit

50 Bài tập Lôgarit Toán 12 mới nhất

Câu 17:

17/06/2026

Tập nghiệm của bất phương trình 2^2x < 2^x+6 là:

Xem đáp án

Đáp án B.

Ta có

Câu 18:

17/06/2026

Tổng giá trị tất cả các nghiệm của phương trình log₃x.log₉x.log₂₇x.log₈₁x $= \frac{2}{3}$ bằng

Xem đáp án

Đáp án A.

Điều kiện: x > 0. Ta có

Câu 19:

17/06/2026

Có bao nhiêu giá trị nguyên dương của tham số m để phương trình 16^x – 2.12^x + (m – 2).9^x = 0 có nghiệm dương?

A. 1.

B. 2.

C. 4.

D. 3.

Xem đáp án

Đáp án B.

<=> t² – 2t – 2 = –m

Dựa vào đồ thị ta thấy PT có nghiệm lớn hơn 1 <=> –m > –3 <=> m < 3

Vậy có 2 giá trị nguyên của m là m = l; m = 2 thỏa mãn yêu cầu bài toán.

Câu 20:

17/06/2026

Cho dãy số (u_n) thỏa mãn $\log u_{1} + \sqrt{2 + \log u_{1} - 2 \log u_{10}} = 2 \log u_{10}$ và u_n+1 = 2u_n với mọi $n \geq 1$ . Giá trị nhỏ nhất của n để u_n > 5¹⁰⁰ bằng

A. 247.

B. 248.

C. 229.

D. 290.

Xem đáp án

Đáp án B.

Đặt $t = \sqrt{2 + \log u_{1} - 2 \log u_{10}} \geq 0$

$\Leftrightarrow \log u_{1} - 2 \log u_{10} = t^{2} - 2$ ,

khi đó giả thiết trở thành:

$\log u_{1} - 2 \log u_{10} + \sqrt{2 + \log u_{1} - 2 \log u_{10}} = 0$

$\Leftrightarrow t^{2} + t - 2 = 0$

<=> t = 1 hoặc t = -2

$\Rightarrow \log u_{1} - 2 \log u_{10} = - 1$

$\Leftrightarrow \log u_{1} + 1 = 2 \log u_{10}$

$\Leftrightarrow \log (10 u_{1}) = \log {(u_{10})}^{2} \Leftrightarrow 10 u_{1} = {(u_{10})}^{2} (1)$

Mà u_n+1 = 2u_n => u_n là cấp số nhân với công bội q = 2

=> u₁₀ = 2⁹ u₁ (2)

Từ (1), (2) suy ra

$10 u_{1} = {(9^{9} u_{1})}^{2} \Leftrightarrow 2^{18} u_{1}^{2} = 10 u_{1} \Leftrightarrow u_{1} = \frac{10}{2^{18}}$

$\Rightarrow u_{n} = 2^{n - 1} . \frac{10}{2^{18}} = \frac{2^{n} . 10}{2^{19}} .$

Do đó $u_{n} > 5^{100} \Leftrightarrow \frac{2^{n} . 10}{2^{19}} > 5^{100}$

$\Leftrightarrow n > \log_{2} (\frac{5^{100} . 2^{19}}{10}) = - \log_{2} 10 + 100 \log_{2} 5 + 19 \approx 247, 87$

Vậy giá trị n nhỏ nhất thỏa mãn là n = 248.

Câu 21:

17/06/2026

Hàm số y = log₂ (4^x – 2^x + m) có tập xác định là $ℝ$ thì

A. $m < \frac{1}{4}$

B. $m > 0$

C. $m \geq \frac{1}{4}$

D. $m > \frac{1}{4}$

Xem đáp án

Đáp án D

Hàm số có tập xác định là R <=> 4^x – 2^x + m > 0, $\forall x \in ℝ$

$\Leftrightarrow m > 2^{x} - 4^{x} (\forall x \in ℝ)$

Đặt t = 2^x > 0 => m > t – t² $(\forall t > 0)$

$\Leftrightarrow m > \underset{t > 0}{m a x} f (t) \Leftrightarrow m > \frac{1}{4}$ .

Câu 22:

17/06/2026

Bất phương trình log₄ (x + 7) > log₂ (x + 1) có bao nhiêu nghiệm nguyên?

A. 1

B. 2

C. 4

D. 3

Xem đáp án

Đáp án C

ĐK: x > –1

Khi đó PT

$\Leftrightarrow \log_{2^{2}} (x + 7) > \log_{2} (x + 1)$

$\Leftrightarrow \frac{1}{2} \log_{2} (x + 7) > \log_{2} (x + 1)$

$\Leftrightarrow \log_{2} (x + 7) > \log_{2} {(x + 1)}^{2}$

$\Leftrightarrow (x + 7) > {(x + 1)}^{2} \Leftrightarrow x^{2} + x - 6 < 0$

$\Leftrightarrow - 3 < x < 2$

Kết hợp dk => -1<x<2 => x=0; x=1.

Câu 23:

17/06/2026

Cho a > 1. Mệnh đề nào sau đây là đúng?

Xem đáp án

Đáp án B

Do a > 1 => với m > n thì a^m > aⁿ

^{$D o - \sqrt{3} > - \sqrt{5} \Rightarrow a^{- \sqrt{3}} > a^{- \sqrt{5}} = \frac{1}{a^{\sqrt{5}}}$ .}

Câu 24:

17/06/2026

Tìm tất cả các giá trị của m để hàm số y = log₃ (–x² + mx + 2m + 1) xác định với mọi $x \in (1; 2)$

A. $m \geq - \frac{1}{3}$

B. $m \geq \frac{3}{4}$

C. $m > \frac{3}{4}$

D. $m < - \frac{1}{3}$

Xem đáp án

Đáp án B

Hàm số xác định với mọi $x \in (1; 2)$

<=> –x² + mx + 2m + 1 > 0 $(\forall x \in (1; 2))$

$X é t g (x) = \frac{x^{2} - 1}{x + 2} v ớ i x \in (1; 2) c ó :$

$g (x) = \frac{x^{2} - 1}{x + 2} = x - 2 + \frac{3}{x + 2}$

$\Rightarrow g^{'} (x) = 1 - \frac{3}{{(x + 2)}^{2}} > 0 (\forall x \in (1; 2))$

Do đó g(x) đồng biến trên khoảng (1;2)

$\Rightarrow m \geq g (2) = \frac{3}{4}$ là giá trị cần tìm.

Câu 25:

17/06/2026

Đạo hàm của hàm số $y = \frac{x + 1}{2^{x}}$ là:

Xem đáp án

Đáp án B

Câu 26:

17/06/2026

Cho a, b là các số dương phân biệt khác 1 và thỏa mãn ab = 1. Khẳng định nào sau đây đúng?

A. log_a b = 1

B. log_a (b+1) < 0

C. log_a b = –1

D. log_a (b+1) > 0

Xem đáp án

Đáp án C

log_a ab = log_a 1 <=> 1 + log_a b = 0 <=> log_a b = –1.

Câu 27:

17/06/2026

Trong mặt phẳng tọa độ Oxy xét hai hình H₁, H₂ được xác định như sau:

$H_{1} = \{M (x; y) | \log (1 + x^{2} + y^{2}) \leq 1 + \log (x + y)\}$

$H_{2} = \{M (x; y) | \log (2 + x^{2} + y^{2}) \leq 2 + \log (x + y)\}$

Gọi S₁, S₂ lần lượt là diện tích của các hình H₁, H₂. Tính tỉ số $\frac{S_{1}}{S_{2}}$

A. 99

B. 101

C. 102

D. 100

Xem đáp án

Đáp án C

Điều kiện x + y > 0

Ta có

$\log (1 + x^{2} + y^{2}) \leq 1 + \log (x + y) = \log [10 (x + y)]$

$\Leftrightarrow 1 + x^{2} + y^{2} \leq 10 (x + y)$

$\Leftrightarrow {(x - 5)}^{2} + {(y - 5)}^{2} \leq 49$

Xét riêng ${(x - 5)}^{2} + {(y - 5)}^{2} \leq 49$ là hình tròn tâm I(5;5) bán kính R=7, diện tích H₁ là diện tích của hình tròn tâm I(5;5) bán kinh R=7, nằm phía trên đường thẳng $∆ : x + y = 0$

$V ì d (I, ∆) = 5 \sqrt{2} > R \Rightarrow S_{1} = 49 π$

Tương tự

$\log (2 + x^{2} + y^{2}) \leq 2 + \log (x + y) = \log [100 (x + y)]$

$\Leftrightarrow 2 + x^{2} + y^{2} \leq 100 (x + y)$

$\Leftrightarrow {(x - 50)}^{2} + {(y - 50)}^{2} \leq 4998$

Xét riêng ${(x - 50)}^{2} + {(y - 50)}^{2} \leq 4998$ là hình tròn tâm I^’(50;50) bán kinh $R = 7 \sqrt{102}$ diện tích H₂ là diện tích của hình tròn tâm I^’(50;50) bán kính $R = 7 \sqrt{102}$ nằm phía trên đường thẳng $∆ : x + y = 0$

$V ì d^{'} (I^{'}; ∆) = 50 \sqrt{2} > R^{'} \Rightarrow S_{2} = 4998 π$

$\Rightarrow \frac{S_{2}}{S_{1}} = 102$ .

Câu 28:

17/06/2026

Cho các số thực x, y, z thỏa mãn $y = 10^{\frac{1}{1 - \log x}}, z = 10^{\frac{1}{1 - \log y}}$ . Mệnh đề nào sau đây đúng?

Xem đáp án

Đáp án D

$\Leftrightarrow \frac{\log z - 1}{\log z} = \frac{1}{1 - \log x}$

$\Leftrightarrow 1 - \log x = \frac{\log z}{\log z - 1}$

$\Leftrightarrow \log x = \frac{- 1}{\log z - 1} \Leftrightarrow x = 10^{\frac{1}{1 - \log z}}$ .

Câu 29:

17/06/2026

Cho x, y là các số thực dương thỏa mãn $\ln x + \ln y \geq \ln (x^{2} + y)$ . Tính giá trị nhỏ nhất của P = x + y.

Xem đáp án

Đáp án B

Ta có $\ln x y = \ln x + \ln y \geq \ln (x^{2} + y)$

$\Leftrightarrow x y \geq x^{2} + y \Leftrightarrow y (x - 1) \geq x^{2}$

Vì x = 1 không thỏa và y > 0 => x > 1

$\Rightarrow P = x y \geq \frac{x^{2}}{x - 1} + x = f (x)$

$X é t h à m s ố f (x) = \frac{x^{2}}{x - 1} + x v ớ i x > 1$

$\Rightarrow f^{'} (x) = \frac{x^{2} - 2 x}{{(x - 1)}^{2}} + x = \frac{2 x^{2} - 4 x + 1}{{(x - 1)}^{2}}$

$\Rightarrow f^{'} (x) = 0 \Leftrightarrow x = \frac{2 + \sqrt{2}}{2} v ì x > 1$

Dựa vào bảng biến thiên của hàm số f(x) suy ra

$\Rightarrow M i n P = \underset{x > 1}{M i n} f (x) = f (1) = 3 + 2 \sqrt{2}$ .

Câu 30:

17/06/2026

Cho biểu thức $P = \sqrt[4]{x^{5}}$ , với x > 0. Mệnh đề nào dưới đây là mệnh đề đúng?

A. $P = x^{20}$

B. $P = x^{\frac{4}{5}}$

C. $P = x^{9}$

D. $P = x^{\frac{5}{4}}$

Xem đáp án

Đáp án D.

$T a c ó : P = \sqrt[4]{x^{5}} = x^{\frac{5}{4}}$ .

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3