Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 2)
-
1564 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
14/07/2024Cho hai số thực dương x,y thỏa mãn 2x + 2y = 4. Tìm giá trị lớn nhất Pmax của biểu thức
P = (2x2 + y)(2y2 + x) + 9xy.
 Xem đáp án
Xem đáp án
Đáp án B.
Ta có
Suy ra
Khi đó
Vậy Pmax = 18 khi x = y = 1.
Câu 2:
16/07/2024Số nghiệm của phương trình
là:
 Xem đáp án
Xem đáp án
Đáp án D.
Điều kiện x > 0. Phương trình đã cho tương đương với:
Câu 4:
13/07/2024Cho ; với a,b là các số thực lớn hơn 1. Khi đó logab c là:
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có
.
Câu 5:
13/07/2024Hàm số y = ln(x2 – 2x + m) có tập xác định là khi:
 Xem đáp án
Xem đáp án
Đáp án A.
Hàm số xác định trên R
Câu 6:
20/07/2024Số nghiệm của phương trình 9x + 2(x – 2).3x + 2x – 5 = 0 là:
 Xem đáp án
Xem đáp án
Đáp án B.
Đặt 3x = t > 0.
Phương trình <=> t2 + 2(x – 2)t + 2x – 5 = 0
Có f(x) = 3x là hàm số đồng biến trên
g(x) = –2x + 5 là hàm số nghịch biến trên
=> Phương trình (*) ó f(x) = g(x) có nhiều nhất l nghiệm
Có f(1) = g(1) => x = 1 là nghiệm của phương trình.
Câu 7:
22/07/2024Số nghiệm nghiệm nguyên nhỏ hơn 2018 của bất phương trình: là:
 Xem đáp án
Xem đáp án
Đáp án A.
+ Điều kiện: x > 0
Bất phương trình
=> Bất phương trình
Từ (1) và (2) => Tập nghiệm của bất phương trình là
S = .
Vậy có 2016 nghiệm nguyên thỏa mãn.
Câu 8:
21/07/2024Tập xác định D của hàm số là:
 Xem đáp án
Xem đáp án
Đáp án C.
Do hàm có là mũ không nguyên nên hàm số xác định khi x > 0
Câu 9:
15/07/2024Cho a, b là các số thực dương thỏa mãn . Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án D
.
Câu 11:
21/07/2024Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD có diện tích là 36, đường thẳng chứa cạnh AB song song với Ox, các đỉnh A, B, C lần lượt nằm trên các đồ thị hàm số y = loga x, , với a là số thực lớn hơn 1. Tìm a.
 Xem đáp án
Xem đáp án
Đáp án D.
Do AB//Ox => A, B nằm trên đường thẳng y = m
Do SABCD = 36
.
Câu 12:
14/07/2024Cho hàm số . Gọi m là giá trị thực để y’(2) = 6mln5. Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án B.
Câu 13:
17/07/2024Cho phương trình . Tìm tham số m để phương trình có 2 nghiệm x1, x2 thỏa mãn x1.x2 = 3.
 Xem đáp án
Xem đáp án
Đáp án C.
Phương trình viết lại:
Đặt t = log3 x => t1 + t2 = log3 x1 + log3 x2 = log3 (x1x2 )= 1
thỏa mãn điều kiện có nghiệm.
Câu 14:
16/07/2024Cho log9 x = log12 y=log16 (x+y). Giá trị của tỉ số là:
 Xem đáp án
Xem đáp án
Đáp án A.
Đặt log9 x = log12 y = log16 (x+y) = a => x = 9a; y = 12a; x + y = 16a
=> 9a + 12a = 16a
Câu 16:
16/07/2024Cho bất phương trình . Đặt ta được bất phương trình nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án C.
Bất phương trình
.
Câu 17:
19/07/2024Giải bất phương trình log4(x2 – x – 8) < 1 + log3 x được tập nghiệm là một khoảng trên trục số có độ dài là:
 Xem đáp án
Xem đáp án
Đáp án B.
Điều kiện
Đặt t = log3x <=> x = 3t
Ta có bất phương trình: 9t < 4.4t + + 8
Hàm số nghịch biến và f(2) = 1 nên ta có t < 2 tìm được tập nghiệm là có độ dài trên trục số là .
Câu 18:
21/07/2024Khẳng định nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án C.
Hàm số đồng biến do cơ số
nên C sai.
Câu 19:
19/07/2024Giá trị của m để phương trình có nghiệm duy nhất là:
 Xem đáp án
Xem đáp án
Đáp án D.
Điều kiện cần để phương trình có nghiệm duy nhất là m
Do thay x bởi –x thì phương trình không đổi nên điều kiện cần để phương trình có nghiệm duy nhất là x = 0 => m = –1
Thử lại với m = –1 thỏa mãn nên D đúng.
Câu 20:
22/07/2024Tập nghiệm của bất phương trình là thì a + b + c là:
 Xem đáp án
Xem đáp án
Đáp án C.
Đặt log x = t, bất phương trình
=> a + b + c =110.
Câu 22:
16/07/2024Số nghiệm nguyên của bất phương trình là:
 Xem đáp án
Xem đáp án
Đáp án A.
Bất phương trình
.
Câu 23:
23/07/2024Cho a, b, c dương thỏa mãn 2a = 3b = 18c. Khi đó biểu thức có giá trị là:
 Xem đáp án
Xem đáp án
Đáp án C
Đặt 2a = 3b = 18c = t
=> a = log2t, b = log3t, c = log18t
Câu 24:
19/07/2024Trong các hàm số dưới đây, hàm số nào đồng biến trên .
 Xem đáp án
Xem đáp án
Đáp án D
Tính đạo hàm và tìm tấp xác định của 3 hàm số trong đáp án A, B, C đều sai.
Ta có .
Câu 25:
13/07/2024Cho các số thực dương a, b, c với . Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án D.
Ta có
=> D sai.
Câu 26:
15/07/2024Cho n > 1 là một số nguyên. Giá trị biểu thức bằng:
 Xem đáp án
Xem đáp án
Đáp án D
= logn! (2.3....n) = logn! n! = 1.
Câu 28:
22/07/2024Cho 9x + 9–x = 23. Tính 3x + 3–x.
 Xem đáp án
Xem đáp án
Đáp án A.
Ta có (3x + 3–x)2 = 9x + 9–x + 2= 23 + 2 = 25
=> 3x + 3–x = 5 vì 3x + 3–x > 0.
Câu 29:
10/11/2024Cho x, y là các số thực lớn hơn 1 thỏa mãn x2 + 9y2 = 6xy. Tính .
 Xem đáp án
Xem đáp án
Đáp án đúng là A.
Lời giải
Ta có x2 + 9y2 = 6xy <=> (x – 3y)2 = 0 <=> x = 3y.
.
*Phương pháp giải:
Biển đổi điều kiện đề bài và sử dụng công thức logarit rút gọn biểu thức cần tìm
*Lý thuyết :
Hàm số logarit
- Hàm số logarit cơ số là hàm số có dạng .
- Hàm số logarit có đạo hàm tại và
(đặc biệt )
- Giới hạn liên quan .
- Đạo hàm:
(đặc biệt )
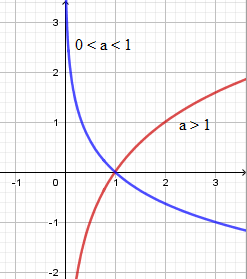
Khảo sát :
- TXĐ:
- Chiều biến thiên:
+ Nếu thì hàm đồng biến trên .
+ Nếu thì hàm nghịch biến trên .
- Đồ thị:
+ Đồ thị hàm số có tiệm cận đứng .
+ Đồ thị hàm số luôn đi qua các điểm và .
+ Đồ thị nằm hoàn toàn phía bên phải trục tung vì .
+ Dáng đồ thị:
Xem thêm
Điều kiện logarit | Lý thuyết, công thức, các dạng bài tập và cách giải
TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12
Câu 30:
19/07/2024Phương trình log2 (x – 1) = 2 có nghiệm là:
 Xem đáp án
Xem đáp án
Đáp án C.
log2 (x – 1) = 2
Bài thi liên quan
-
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 1)
-
30 câu hỏi
-
30 phút
-
-
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 3)
-
30 câu hỏi
-
30 phút
-
-
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 4)
-
30 câu hỏi
-
30 phút
-
-
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 5)
-
30 câu hỏi
-
30 phút
-
-
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 6)
-
30 câu hỏi
-
30 phút
-
-
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 7)
-
30 câu hỏi
-
30 phút
-
-
Bài tập Hàm số mũ, logarit ôn thi THPT Quốc gia có lời giải (P1) (Đề 8)
-
30 câu hỏi
-
30 phút
-
