27 câu hỏi trắc nghiệm thuộc 244 Bài trắc nghiệm mũ và hàm số lũy thừa cực hay có lời giải (P1) (Đề 2)

Câu 1:

14/07/2024

Tập xác định của hàm số $y = {(x^{2} - 3 x + 2)}^{- 3}$ là

A. R \ {1; 2}

B. $(- \infty; 1) \cup (2; + \infty)$

C. (1; 2)

D. R

Xem đáp án

Câu 2:

22/07/2024

Tập xác định của hàm số $y = {(- 2 x^{2} - x + 3)}^{2 e - 1}$

A. R \ ${- \frac{3}{2}; 1}$

B. $(- \infty; - \frac{3}{2}) \cup (1; + \infty)$

C. $(- \frac{3}{2}; 1)$

D. R

Xem đáp án

Câu 3:

21/07/2024

Tập xác định của hàm số $y = {(x - 2)}^{- 5}$ là

A. $(- \infty; 2)$

B. $(2; + \infty)$

C. R

D. R \ {2}

Xem đáp án

Câu 4:

14/07/2024

Tập xác định của hàm số $y = {(2 x - x^{2})}^{\frac{2}{3}}$ là

A. R \ {0; 2}

B. (0; 2)

C. R

D. $(- \infty; 0) \cup (2; + \infty)$

Xem đáp án

Câu 5:

06/11/2024

Trong các hàm số sau, hàm số nào là hàm lũy thừa?

A. $f (x) = \sqrt[3]{x}$

B. $f (x) = 4^{x}$

C. $f (x) = e^{x}$

D. $f (x) = x^{\frac{1}{3}}$

Xem đáp án

Đáp án đúng là D

*Lời giải:

*Phương pháp giải:

- căn cứ vào khái niệm hàm lũy thừa để xác định

* Các lý thuyết thêm và các dạng bài toán về hàm số lũy thừa:

Hàm số lũy thừa

+ Khái niệm: Hàm số $y = x^{α}$ , với $α \in ℝ$ , được gọi là hàm số lũy thừa.

+ Tập xác định: Tập xác định của hàm số lũy thừa $y = x^{α}$ tùy thuộc vào giá trị của $α$ .

Cụ thể:

- Với $α$ nguyên dương, tập xác định là R.

- Với $α$ nguyên âm hoặc bằng 0, tập xác định là $ℝ \ \{0\}$ .

- Với không nguyên, tập xác định .

+ Đạo hàm:

${(x^{α})}^{'} = α . x^{α - 1}$

u = u(x) $\Rightarrow {(u^{α})}^{'} = α . u^{'} . u^{α - 1}$

+ Sự biến thiên của hàm số $y = x^{α}$ trong khoảng $(0; + \infty)$

Với > 0: Hàm số đồng biến trong khoảng $(0; + \infty)$

Với < 0: Hàm số nghịch biến trong khoảng $(0; + \infty)$

+ Đồ thị hàm số $y = x^{α}$ trong khoảng $(0; + \infty)$

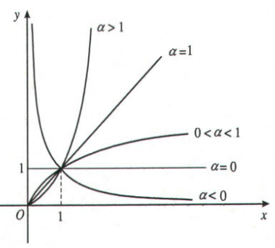
Đồ thị của hàm số lũy thừa $y = x^{α}$ luôn đi qua điểm I(1,1).

2. Hàm số mũ

Hàm số có dạng $y = a^{x}$ , $0 < a \neq 1$ được gọi là hàm số mũ.

+ Tập xác định: $D = ℝ$ .

+ Tập giá trị: $T = (0; + \infty)$ .

+ Sự biến thiên:

Khi a > 1 hàm số đồng biến trên khoảng $(- \infty; + \infty)$

Khi 0 < a < 1 hàm số nghịch biến trên khoảng $(- \infty; + \infty)$

+ Đồ thị nhận trục hoành làm tiệm cận ngang.

+ Đạo hàm:

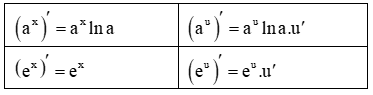
3. Hàm số logarit

Hàm số có dạng $y = \log_{a} x$ $(0 < a \neq 1)$

Tập xác định: $D = (0; + \infty)$

Tập giá trị: $T = ℝ$ .

Đạo hàm:

Sự biến thiên: Khi a > 1 hàm số đồng biến trên khoảng $(0; + \infty)$ ,

Khi 0 < a < 1 hàm số nghịch biến trên khoảng $(0; + \infty)$ .

CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1: Tìm tập xác định của hàm số.

- Tìm tập xác định của hàm số lũy thừa: $y = u {(x)}^{α}, \forall α \in ℝ$

Nếu $α \in ℤ^{+}$ , hàm số xác định khi u(x)xác định.

Nếu $[\begin{array}{l} α \in ℤ^{-} \\ α = 0 \end{array}$ , hàm số xác định khi $u (x) \neq 0$ .

Nếu $α \notin ℤ$ , hàm số xác định khi u(x) > 0.

- Tìm tập xác định của hàm số logarit:

Dựa vào định nghĩa logarit logab xác định $\Leftrightarrow \{\begin{cases} a > 0, a \neq 1 \\ b > 0 \end{cases}$

Dạng 2: Tính đạo hàm của hàm số.

Dạng 3: Khảo sát sự biến thiên và đồ thị của hàm số.

- Sự biến thiên của các hàm số: Áp dụng tính chất:

a) Hàm số lũy thừa $y = x^{α}$ trong khoảng $(0; + \infty)$

Với > 0: Hàm số đồng biến trong khoảng $(0; + \infty)$

Với < 0: Hàm số nghịch biến trong khoảng $(0; + \infty)$

b) Hàm số mũ: $y = a^{x} (a > 0, a \neq 1)$ . Tập xác định: R.

Nếu a > 1: hàm số luôn đồng biến.

Nếu 0 < a < 1: hàm số luôn nghịch biến.

c) Hàm số logarit $y = \log_{a} x (a > 0, a \neq 1)$ . Tập xác định: $(0; + \infty)$

Nếu a > 1: hàm số đồng biến $(0; + \infty)$

Nếu 0 < a < 1: hàm số nghịch biến $(0; + \infty)$

- Đồ thị của các hàm số.

B1: Dựa vào tính đơn điệu của hàm số.

B2: Đồ thị của hàm số lũy thừa $y = x^{α}$ luôn đi qua điểm I(1,1).

Đồ thị hàm số mũ $y = a^{x}$ đi qua điểm $A (1; a)$ .

Đồ thị hàm số đi $y = \log_{a} x$ qua điểm $B (a; 1)$ .

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hàm số lũy thừa (mới 2024 + Bài Tập) – Toán 12

TOP 40 câu Trắc nghiệm Hàm lũy thừa (có đáp án 2024) - Toán 12

50 bài toán về hàm số lũy thừa, hàm số mũ, hàm số logarit và cách giải (có đáp án 2024) – Toán 12

Câu 6:

23/07/2024

Tập xác định của hàm số $y = {(x - 1)}^{- 4}$ là

A. $[1; + \infty)$

B. R

C. $(1; + \infty)$

D. R \ {1}

Xem đáp án

Câu 7:

22/07/2024

Tìm tập xác định D của hàm số $y = \log_{2019} (4 - x^{2}) + {(2 x - 3)}^{- 2019}$

A. $[- 2; \frac{3}{2}) \cup (\frac{3}{2}; 2]$

B. $(- 2; \frac{3}{2}) \cup (\frac{3}{2}; 2)$

C. $(\frac{3}{2}; 2)$

D. (-2; 2)

Xem đáp án

Câu 8:

14/07/2024

Tập xác định của hàm số $y = {(- x^{2} + 3 x + 4)}^{\frac{1}{3}} + \sqrt{2 - x}$ là

A. (-1; 2]

B. (-1; 2)

C. $(- \infty; 2]$

D. [-1; 2]

Xem đáp án

Câu 9:

14/07/2024

Tập xác định của hàm số $y = {(x - 1)}^{\frac{1}{5}}$ là

A. $(1; + \infty)$

B. $[1; + \infty)$

C. $(0; + \infty)$

D. R \ {1}

Xem đáp án

Câu 10:

23/07/2024

Tìm tập xác định D của hàm số $y = {(x^{2} - 3 x - 4)}^{\sqrt{2 - \sqrt{3}}}$

A. D = R \ {-1; 4}

B. D = $(- \infty; - 1] \cup [4; + \infty)$

C. D = R

D. D = $(- \infty; - 1) \cup (4; + \infty)$

Xem đáp án

Câu 11:

22/07/2024

Tìm tập xác định D của hàm số y $y = {(4 - x^{2})}^{\frac{1}{5}}$

A. D = [-2; 2]

B. D = R \ { $\pm 2$ }

C. D = (-2; 2)

D. D = $(- \infty; + \infty)$

Xem đáp án

Câu 12:

14/07/2024

Tập xác định của hàm số $y = {(3 x - 5)}^{\frac{1}{3}}$ là

A. R \ ${\frac{5}{3}}$

B. R

C. $(\frac{5}{3}; + \infty)$

D. $[\frac{5}{3}; + \infty)$

Xem đáp án

Câu 13:

14/07/2024

Có bao nhiêu giá trị m nguyên để hàm số $y = {(2 x^{2} + m x + 2)}^{\frac{3}{2}}$ xác định với mọi $x \in R$ ?

A. 5

B. 4

C. 7

D. 9

Xem đáp án

Câu 14:

21/07/2024

Cho biết phương trình $\log_{9} x + \sqrt{\log_{9} x + 4} = 26$ có nghiệm dạng $x = 3^{n}$ , với n là số tự nhiên. Tổng tất cả các chữ số của n bằng

A. 9

B. 5

C. 6

D. 3

Xem đáp án

Câu 15:

14/07/2024

Tập xác định của hàm số $y = {(x + 3)}^{\frac{3}{2}} - \sqrt[4]{5 - x}$ là

A. D = (-3; 5]

B. D = $(- 3; + \infty) \ {5}$

C. D = (-3; 5)

D. D = $(- 3; + \infty)$

Xem đáp án

Câu 16:

14/07/2024

Tập xác định của hàm số $y = {(x^{2} - 3 x + 2)}^{\frac{3}{5}} + {(x - 3)}^{- 2}$ là

A. D= $(- \infty; + \infty) \ {3}$

B. D = $(- \infty; 1) \cup (2; + \infty) \ {3}$

C. D = $(- \infty; + \infty) \ (1; 2)$

D. D = $(- \infty; 1) \cup (2; + \infty)$

Xem đáp án

Câu 17:

23/07/2024

Tập xác định của hàm số $y = {(x^{2} - 4 x)}^{e}$ là

A. R

B. R \ {0; 4}

C. $(- \infty; 0) \cup (4; + \infty)$

D. $(3; + \infty)$

Xem đáp án

Câu 18:

12/10/2024

Hàm số nào sau đây có tập xác định là R ?

A. y = $x^{\frac{1}{3}}$

B. y = $\ln |x|$

C. y = $2^{\frac{1}{x}}$

D. y = $\frac{1}{e^{x}}$

Xem đáp án

*Phương pháp giải:

- Hàm số y = a^x (a > 0, a ≠ 1) có tập xác định D = ℝ.

- Hàm số mũ y = a^f(x) (a > 0, a ≠ 1) xác định khi f(x) xác định.

*Lời giải:

* Một số lý thuyết liên quan:

Hàm số lôgarit

- Hàm số y = log_af(x) xác định $\Leftrightarrow \{\begin{cases} 0 < a \neq 1 \\ f(x) > 0 \end{cases}$

- Hàm số y = log_g(x)f(x) xác định $\Leftrightarrow \{\begin{cases} 0 < g(x) \neq 1 \\ f(x) > 0 \end{cases}$

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hàm số mũ. Hàm số logarit (năm 2024 + Bài Tập)– Toán 12

Tìm tập xác định của các hàm số

100 bài tập về tìm tập xác định của hàm số mũ và cách giải (2024)

Câu 19:

22/07/2024

Cho a > 0, $a \neq 1$ . Tìm mệnh đề đúng trong các mệnh đề sau

A. Tập giá trị của hàm số $y = a^{x}$ là tập R

B. Tập giá trị của hàm số $y = \log_{a} x$ là tập R

C. Tập xác định của hàm số $y = \log_{a} x$ là tập R

D. Tập xác định của hàm số $y = \log_{a} x$ là khoảng $(0; + \infty)$

Xem đáp án

Câu 20:

20/07/2024

Tập xác định của hàm số $y = \log_{2} (x^{2} - 7 x + 10)$ là

A. (2; 5)

B. $(- \infty; 2) \cup (5; + \infty)$

C. $(- \infty; 2] \cup [5; + \infty)$

D. [2; 5]

Xem đáp án

Câu 21:

22/07/2024

Hàm số $y = \log_{2} (2 x - 3)$ có tập xác định là

A. D = R

B. D = $[\frac{3}{2}; + \infty)$

C. D = $R \ {\frac{3}{2}}$

D. D = $(\frac{3}{2}; + \infty)$

Xem đáp án

Câu 22:

21/07/2024

Tập xác định của hàm số $y = \log_{\frac{1}{3}} (4 - 2 x)$ là

A. $(- \infty; 2)$

B. $[2; + \infty)$

C. $(- \infty; 2]$

D. $(2; + \infty)$

Xem đáp án

Câu 23:

22/07/2024

Với giá trị nào của x thì biểu thức $B = \log_{2} (2 x - 1)$ xác định?

A. $x \in (- 1; + \infty)$

B. $x \in (- \infty; \frac{1}{2})$

C. $x \in R \ {\frac{1}{2}}$

D. $x \in (\frac{1}{2}; + \infty)$

Xem đáp án

Câu 24:

16/07/2024

Tìm tập xác định của hàm số $y = {(x^{2} - 3 x + 2)}^{π}$ .

A. ( 1; 2)

B. $(- \infty; 1] \cup [2; + \infty)$

C. R \ {1; 2}

D. $(- \infty; 1) \cup (2; + \infty)$

Xem đáp án

Câu 25:

22/07/2024

Tìm tập xác định của hàm số $y = \ln (1 - x)$

A. D = $(- \infty; - 1)$

B. D = $(- 1; + \infty)$

C. D = $(- \infty; 1)$

D. D = $(1; + \infty)$

Xem đáp án

Câu 26:

14/07/2024

Tìm tập xác định của hàm số $y = \frac{1}{\sqrt{\log_{2} (x - 1)}}$

A. (1; 2)

B. $(2; + \infty)$

C. $(1; + \infty)$

D. $(1; + \infty) \ {2}$

Xem đáp án

Câu 27:

18/07/2024

Hàm số $y = \log_{3} \frac{1}{\sqrt{6 - x}}$ có tập xác định là

A. $(6; + \infty)$

B. $(- \infty; 6)$

C. $(0; + \infty)$

D. $(- \infty; + \infty)$

Xem đáp án

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3