Trong các hàm số sau, hàm số nào là hàm lũy thừa?

Đáp án đúng là D

*Lời giải:

*Phương pháp giải:

- căn cứ vào khái niệm hàm lũy thừa để xác định 

* Các lý thuyết thêm và các dạng bài toán về hàm số lũy thừa:

Hàm số lũy thừa

+ Khái niệm: Hàm số $y=x^{\alpha }$, với $\alpha \in R$, được gọi là hàm số lũy thừa.

+ Tập xác định: Tập xác định của hàm số lũy thừa $y=x^{\alpha }$ tùy thuộc vào giá trị của $\alpha$.

Cụ thể:

- Với $\alpha$ nguyên dương, tập xác định là R.

- Với $\alpha$ nguyên âm hoặc bằng 0, tập xác định là $R\backslash \left\{0\right\}$.

- Với không nguyên, tập xác định .

+ Đạo hàm:

${\left(x^{\alpha }\right)}^{\prime }=\alpha .x^{\alpha -1}$

u = u(x) $\Rightarrow {\left(u^{\alpha }\right)}^{\prime }=\alpha .u^{\prime }.u^{\alpha -1}$

+ Sự biến thiên của hàm số $y=x^{\alpha }$ trong khoảng $\left(0;+\infty \right)$

Với > 0: Hàm số đồng biến trong khoảng $\left(0;+\infty \right)$

Với < 0: Hàm số nghịch biến trong khoảng $\left(0;+\infty \right)$

+ Đồ thị hàm số $y=x^{\alpha }$ trong khoảng $\left(0;+\infty \right)$

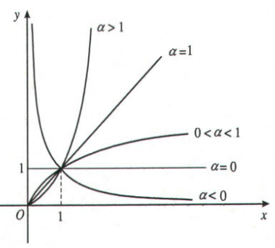
Đồ thị của hàm số lũy thừa $y=x^{\alpha }$ luôn đi qua điểm I(1,1).

2. Hàm số mũ

Hàm số có dạng $y=a^x$, $0<a\ne 1$ được gọi là hàm số mũ.

+ Tập xác định: $D=R$.

+ Tập giá trị: $T=\left(0;+\infty \right)$.

+ Sự biến thiên:

Khi a > 1 hàm số đồng biến trên khoảng $\left(-\infty ;+\infty \right)$

Khi 0 < a < 1 hàm số nghịch biến trên khoảng $\left(-\infty ;+\infty \right)$

+ Đồ thị nhận trục hoành làm tiệm cận ngang.

+ Đạo hàm:

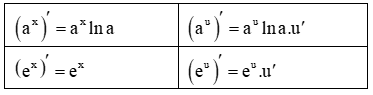
3. Hàm số logarit

Hàm số có dạng $y={\log }_{a}x$ $\left(0<a\ne 1\right)$

Tập xác định: $D=\left(0;+\infty \right)$

Tập giá trị: $T=R$.

Đạo hàm:

Sự biến thiên: Khi a > 1 hàm số đồng biến trên khoảng $\left(0;+\infty \right)$,

Khi 0 < a < 1 hàm số nghịch biến trên khoảng $\left(0;+\infty \right)$.

CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI

Dạng 1: Tìm tập xác định của hàm số.

- Tìm tập xác định của hàm số lũy thừa: $y=u{\left(x\right)}^{\alpha },\forall \alpha \in R$

Nếu $\alpha \in Z^{+}$, hàm số xác định khi u(x)xác định.

Nếu $[\begin{array}{c}\alpha \in Z^{-}\\ \alpha =0\end{array}$, hàm số xác định khi $u\left(x\right)\ne 0$.

Nếu $\alpha \notin Z$, hàm số xác định khi u(x) > 0.

- Tìm tập xác định của hàm số logarit:

Dựa vào định nghĩa logarit logab xác định$\iff \{\begin{array}{c}a>0,a\ne 1\\ b>0\end{array}$

Dạng 2: Tính đạo hàm của hàm số.

Dạng 3: Khảo sát sự biến thiên và đồ thị của hàm số.

- Sự biến thiên của các hàm số: Áp dụng tính chất:

a) Hàm số lũy thừa $y=x^{\alpha }$ trong khoảng $\left(0;+\infty \right)$

Với > 0: Hàm số đồng biến trong khoảng $\left(0;+\infty \right)$

Với < 0: Hàm số nghịch biến trong khoảng $\left(0;+\infty \right)$

b) Hàm số mũ: $y=a^x\left(a>0,a\ne 1\right)$. Tập xác định: R.

Nếu a > 1: hàm số luôn đồng biến.

Nếu 0 < a < 1: hàm số luôn nghịch biến.

c) Hàm số logarit $y={\log }_{a}x\left(a>0,a\ne 1\right)$. Tập xác định: $\left(0;+\infty \right)$

Nếu a > 1: hàm số đồng biến $\left(0;+\infty \right)$

Nếu 0 < a < 1: hàm số nghịch biến $\left(0;+\infty \right)$

- Đồ thị của các hàm số.

B1: Dựa vào tính đơn điệu của hàm số.

B2: Đồ thị của hàm số lũy thừa $y=x^{\alpha }$ luôn đi qua điểm I(1,1).

Đồ thị hàm số mũ $y=a^x$ đi qua điểm $A\left(1;a\right)$.

 

Đồ thị hàm số đi $y={\log }_{a}x$ qua điểm $B\left(a;1\right)$.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hàm số lũy thừa (mới 2024 + Bài Tập) – Toán 12

TOP 40 câu Trắc nghiệm Hàm lũy thừa (có đáp án 2024) - Toán 12

50 bài toán về hàm số lũy thừa, hàm số mũ, hàm số logarit và cách giải (có đáp án 2024) – Toán 12