27 câu hỏi trắc nghiệm thuộc 244 Bài trắc nghiệm mũ và hàm số lũy thừa cực hay có lời giải (P1) (Đề 3)

Tập xác định của hàm số $y = \log \frac{3 - x}{x - 1}$ là

A. $(3; + \infty)$

B. (1; 3)

C. $(- \infty; 1) \cup (3; + \infty)$

D. R \ {1}

Xem đáp án

Câu 2:

22/07/2024

Tập xác định của hàm số $y = \log (2 x - x^{2})$ là

A. D = [0;2]

B. D = $(- \infty; 0] \cup [2; + \infty)$

C. D = $(- \infty; 0) \cup (2; + \infty)$

D. D = (0; 2)

Xem đáp án

Câu 3:

Tìm tập xác định của hàm số $y = \log_{2} (x^{2} - x)$ là

A. [0; 1]

B. (0; 1)

C. $(- \infty; 0] \cup [1; + \infty)$

D. $(- \infty; 0) \cup (1; + \infty)$

Xem đáp án

Câu 4:

Tập xác định của hàm số $y = {(x^{2} - 3 x + 2)}^{π}$ là

A. $(- \infty; 1) \cup (2; + \infty)$

B. R

C. $(0; + \infty)$

D. (1; 2)

Xem đáp án

Câu 5:

Tập xác định của hàm số $y = \log_{3} (3 - 2 x)$ là

A. R

B. $(\frac{3}{2}; + \infty)$

C. $(- \infty; \frac{3}{2})$

D. $(- \infty; \frac{3}{2}]$

Xem đáp án

Câu 6:

Tập xác định của hàm số $y = \frac{1}{5^{x}}$ là

A. $(0; + \infty)$

B. $[0; + \infty)$

C. $R \ {0}$

D. R

Xem đáp án

Câu 7:

Tập xác định của hàm số $y = {[\ln (x - 2)]}^{π}$ là

A. R

B. $(3; + \infty)$

C. $(0; + \infty)$

D. $(2; + \infty)$

Xem đáp án

Câu 8:

Khẳng định nào dưới đây là sai khi nói về hàm số $y = \log_{a} x (v ớ i 0 < a \neq 1)$ ?

A. Trên tập xác định, hàm số đồng biến nếu a > 1, nghịch biến nếu 0<a<1

B. Đồ thị hàm số có một tiệm cận đứng và không có tiệm cận ngang

C. Tập xác định của hàm số là R

D. Đồ thị hàm số luôn nằm bên phải trục tung

Xem đáp án

Câu 9:

Tập xác định của hàm số $y = \log_{2} (x^{2} - 2 x)$ là

A. $(- \infty; 0) \cup (2; + \infty)$

B. [0; 2]

C. $(- \infty; 0] \cup [2; + \infty)$

D. (0; 2)

Xem đáp án

Câu 10:

16/07/2024

Hàm số nào dưới đây nghịch biến trên tập xác định của nó?

A. $y = \log_{\sqrt{3}} x$

B. $y = \log_{2} (\sqrt{x} + 1)$

C. $y = \log_{\frac{π}{4}} x$

D. $y = {(\frac{π}{3})}^{x}$

Xem đáp án

Câu 11:

Tập xác định D của hàm số $y = \log_{2} (x + 1)$ là

A. D = $(0; + \infty)$

B. D = $(- 1; + \infty)$

C. D = $[- 1; + \infty)$

D. D = $[0; + \infty)$

Xem đáp án

Câu 12:

Tìm tập xác định D của hàm số $y = \log_{3} (x^{2} - 6 x + 8)$

A. D = [2; 4]

B. D = $(- \infty; 2) \cup (4; + \infty)$

C. D = $(- \infty; 2] \cup [4; + \infty)$

D. D = (2; 4)

Xem đáp án

Câu 13:

Tìm tập xác định của hàm số $y = \log (x^{2} - x - 2)$

A. $(- \infty; - 1) \cup (2; + \infty)$

B. $(- \infty; 2)$

C. $(1; + \infty)$

D. (-1; 1)

Xem đáp án

Câu 14:

Tập xác định của hàm số $y = \log_{2} \frac{3 - x}{2 x}$ là

A. $(3; + \infty)$

B. $(0; 3]$

C. (0; 3)

D. $(- \infty; 0) \cup (3; + \infty)$

Xem đáp án

Câu 15:

Tập xác định của hàm số

$y = \log (4 x^{2} - 9)$ là

A. D = $(- \frac{3}{2}; \frac{3}{2})$

B. D = $(- \infty; - \frac{3}{2}] \cup [\frac{3}{2}; + \infty)$

C. D = $(- \infty; - \frac{3}{2}) \cup (\frac{3}{2}; + \infty)$

D. D = $[- \frac{3}{2}; \frac{3}{2}]$

Xem đáp án

Câu 16:

18/07/2024

Tìm tập xác định của hàm số $y = \ln {(1 - x)}^{2}$

A. $(1; + \infty)$

B. $(- \infty; 1)$

C. R

D. R \ {1}

Xem đáp án

Câu 17:

Tìm tập xác định của hàm số $y = \ln (2 x^{2} - 5 x + 2)$

A. $(- \infty; \frac{1}{2}] \cup [2; + \infty)$

B. $(\frac{1}{2}; 2)$

C. $(- \infty; \frac{1}{2}) \cup (2; + \infty)$

D. $[\frac{1}{2}; 2]$

Xem đáp án

Câu 18:

22/07/2024

Điều kiện xác định của hàm số $y = \log_{2} (x - 1)$ là

A. $x \neq 1$

B. x > 1

C. x < 1

D. $\forall x \in R$

Xem đáp án

Câu 19:

Trắc nghiệm Sự đồng biến, nghịch biến của hàm số (có đáp án)

Tập hợp các giá trị của x để biểu thức $y = \log_{5} (x^{3} - x^{2} - 2 x)$ có nghĩa là

A. (0; 1)

B. $(- 1; 0) \cup (2; + \infty)$

C. $(1; + \infty)$

D. $(- \infty; - 1)$

Xem đáp án

Câu 20:

12/11/2024

Hàm số nào dưới đây đồng biến trên tập xác định của nó?

A. $y = {(\frac{e}{π})}^{x}$

B. $y = {(\sqrt{2})}^{x}$

C. $y = {(0.5)}^{x}$

D. $y = {(\frac{2}{3})}^{x}$

Xem đáp án

Đáp án đúng: B

*Lời giải:

- Ta xét các hàm số trên: tất cả các cơ số của các hàm mũ chỉ có câu B là > 1

nên hàm số y = ${(\sqrt{2})}^{x}$ đồng biến trên R

*Phương pháp giải:

- Dựa vào tính đơn điệu của hàm số mũ: Cho hàm số y = a^x, (a > 0; a ≠ 1). Khi đó:

Nếu a > 1 thì hàm số đồng biến trên R

Nếu 0 < a < 1 thì hàm số nghịch biến trên R

*Các dạng bài tập thường gặp sự đồng biến/nghịch biến của hàm mũ:

* Phương pháp chung:

Bước 1: Tìm tập xác định D.

Bước 2: Tính đạo hàm y' = f'(x).

Bước 3: Tìm nghiệm của f'(x) hoặc những giá trị x làm cho f'(x) không xác định.

Bước 4: Lập bảng biến thiên.

Bước 5: Kết luận.

- Dựa vào tính đơn điệu của hàm số mũ:

Cho hàm số y = a^x, (a > 0; a ≠ 1). Khi đó:

Nếu a > 1 thì hàm số đồng biến trên R

Nếu 0 < a < 1 thì hàm số nghịch biến trên R

* Dạng bài toán:

Dạng 1: Tìm giá trị của m để hàm số đơn điệu trên R.

* Phương pháp làm bài:

– Bước 1: Tính f′(x).

– Bước 2: Nêu các điều kiện của bài toán:

+ Hàm số y=f(x) đồng biến trên R⇔y′=f′(x)⩾0,với ∀x∈R và y′=0 tại một hữu hạn điểm.

+ Hàm số y=f(x) nghịch biến trên R⇔y′=f′(x)⩽0,với ∀x∈R và y′=0 tại một hữu hạn điểm.

– Bước 3: Từ các điều kiện trên sử dụng các kiến thức về dấu của nhị thức bậc nhất và tam thức bậc hai để tìm m.

Dạng 2: Tìm m để hàm số đơn điệu trên miền D đã cho trước.

* Phương pháp làm bài:

– Bước 1: Nêu các điều kiện để hàm số đơn điệu trên D:

+ Hàm số y=f(x) đồng biến trên D⇔y′=f′(x)⩾0, với ∀x∈D.

+ Hàm số y=f(x) nghịch biến trên D⇔y′=f′(x)⩽0,với ∀x∈D.

– Bước 2: Từ điều kiện trên hãy sử dụng các cách suy luận khác nhau cho từng bài toán để tìm m.

- Bước 3: Kết luận

c) Dạng 4: Tìm m để hàm số đồng biến, nghịch biến trên khoảng

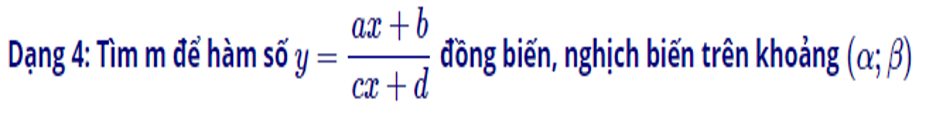
– Bước 1: Tính y′

– Bước 2: Nêu điều kiện để hàm số đồng biến và nghịch biến:

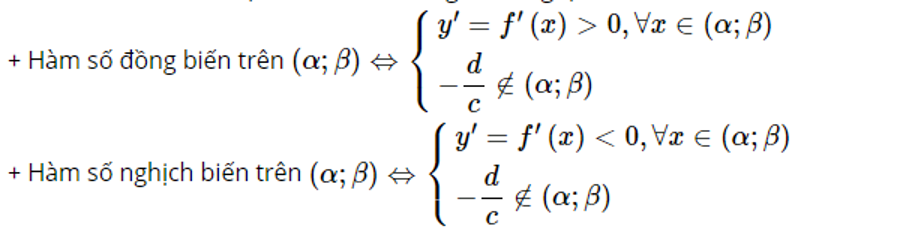
– Bước 3: Đưa ra kết luận.

Xem thêm các bài viết liên quan hay, chi tiết:

Bài tập Sự đồng biến nghịch biến của hàm số Toán 12 mới nhất

Trắc nghiệm Hàm lũy thừa (có đáp án)

Câu 21:

Tập xác định D của hàm số $y = {(x^{3} - 8)}^{\frac{π}{2}}$ là

A. D = $[2; + \infty)$

B. D = R \ {2}

C. D = R

D. D = $(2; + \infty)$

Xem đáp án

Câu 22:

Tìm tập xác định D của hàm số $f (x) = {(4 x - 3)}^{\frac{1}{2}}$ .

A. D = R \ ${\frac{4}{3}}$

B. D = R

C. D = $[\frac{3}{4}; + \infty)$

C. D = $(\frac{3}{4}; + \infty)$

Xem đáp án

Câu 23:

Tập xác định của hàm số $y = \log_{2} (\frac{1 - x}{3 x + 2})$ là?

A. $[- \frac{2}{3}; 1]$

B. $(- \frac{2}{3}; 1)$

C. $(- \infty; - \frac{2}{3}) \cup (1; + \infty)$

D. $(- \infty; - \frac{2}{3}] \cup [1; + \infty)$

Xem đáp án

Câu 24:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = \log (x^{2} - 2 m x + 4)$ có tập xác định là R

A. $- 2 \leq m \leq 2$

B. m = 2

D. -2 < m < 2

Xem đáp án

Câu 25:

Tập xác định của hàm số $y = \ln (- x^{2} + 3 x - 2)$ là

A. $(- \infty; 1] \cup [2; + \infty)$

B. [1; 2]

C. $(- \infty; 1) \cup (2; + \infty)$

D. $(1; 2)$

Xem đáp án

Câu 26: