Giải bài tập trang 39 Chuyên đề Toán 10 Bài 2 - Chân trời sáng tạo
Với Giải bài tập trang 39 Chuyên đề Toán 10 trong Bài 2: Nhị thức Newton sách Chuyên đề Toán lớp 10 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Chuyên đề Toán 10 trang 39.
Giải bài tập trang 39 Chuyên đề Toán 10 Bài 2 - Chân trời sáng tạo
Thực hành 5 trang 39 Chuyên đề Toán 10: Chứng minh rằng, với mọi , ta có
Lời giải:
Xét khai triển:
(1 + x)n =
Thay x = –1 ta được:
(1 – 1)n
Vận dụng trang 39 Chuyên đề Toán 10: Trong hộp A có 10 quả cầu được đánh số từ 1 đến 10. Người ta lấy một số quả cầu từ hộp A rồi cho vào hộp B. Có tất cả bao nhiêu cách lấy, tính cả trường hợp lấy không quả (tức không lấy quả nào)?
Lời giải:
Số cách lấy k quả cầu từ hộp A rồi cho vào hộp B là với 0 ≤ k ≤ 10.
Như vậy có tất cả cách.
Lại có
nên có tổng cộng 1024 cách lấy.
Bài 1 trang 39 Chuyên đề Toán 10:
Khai triển biểu thức:
a) (x – 2y)6;
b) (3x – 1)5.
Lời giải:
Sử dụng tam giác Pascal, ta có:
a) (x – 2y)6
b) (3x – 1)5
Bài 2 trang 39 Chuyên đề Toán 10: Tìm hệ số của x10 trong khai triển của biểu thức (2 – x)12.
Lời giải:
Áp dụng công thức nhị thức Newton, ta có:
(2 – x)12 =
Số hạng chứa x10 ứng với giá trị k = 10. Hệ số của số hạng này là
Bài 3 trang 39 Chuyên đề Toán 10:
Biết rằng a là một số thực khác 0 và trong khai triển của (ax + 1)6, hệ số của x4 gấp bốn lần hệ số của x2. Tìm giá trị của a.
Lời giải:
Áp dụng công thức nhị thức Newton, ta có:
(ax + 1)6 =
Số hạng chứa x4 ứng với giá trị k = 2. Hệ số của số hạng này là
Số hạng chứa x2 ứng với giá trị k = 4. Hệ số của số hạng này là
Theo giả thiết, ta có 15a4 = 4 . 15a2, suy ra a = 2 hoặc a = –2.
Vậy a = 2 hoặc a = –2.
Bài 4 trang 39 Chuyên đề Toán 10:
Biết rằng hệ số của x2 trong khai triển của (1 + 3x)n là 90. Tìm giá trị của n.
Lời giải:
Áp dụng công thức nhị thức Newton, ta có:
(1 + 3x)n =
Số hạng chứa x2 ứng với giá trị k = 2. Hệ số của số hạng này là
Theo giả thiết, ta có
Vậy n = 5.
Bài 5 trang 39 Chuyên đề Toán 10: Chứng minh công thức nhị thức Newton (công thức (1), trang 35 ) bằng phương pháp quy nạp toán học.
Lời giải:
+) Với n = 1, ta có: (a + b)1 = a + b =
Vậy công thức đúng với n = 1.
+) Với k ≥ 1 là một số nguyên dương tuỳ ý mà công thức đúng đúng, ta phải chứng minh công thức cũng đúng với k + 1, tức là:
Thật vậy, theo giả thiết quy nạp ta có:
Khi đó:
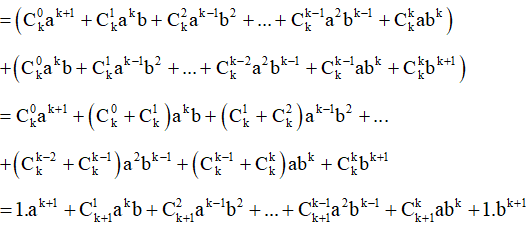
(vì , i ℕ, k ℕ*)
Vậy công thức cũng đúng với n = k + 1. Do đó theo nguyên lí quy nạp toán học, công thức đã cho đúng với mọi n ℕ*.
Bài 6 trang 39 Chuyên đề Toán 10:
Biết rằng (3x – 1)7 = a0 + a1x + a2x2 + a3x3 + a4x4 + a5x5 + a6x6 + a7x7. Hãy tính:
a) a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7;
b) a0 + a2 + a4 + a6.
Lời giải:
Có (3x – 1)7
= 2187x7 – 5103x6 + 5103x5 – 2835x4 + 945x3 – 189x2 + 21x – 1.
a) a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7
= (–1) + 21 + (–189) + 945 + (–2835) + 5103 + (–5103) + 2187 = 128.
b) a0 + a2 + a4 + a6
= (–1) + (–189) + (–2835) + (–5103) = –8128.
Bài 7 trang 39 Chuyên đề Toán 10: Một tập hợp có 12 phần tử thì có tất cả bao nhiêu tập hợp con?
Lời giải:
Vì tập hợp đã cho có 12 phần tử nên số tập hợp con có k phần tử của nó là:
Như vậy tổng số tập con của tập hợp này là:
Lại có
Vậy một tập hợp có 12 phần tử thì có tất cả 4096 tập hợp con.
Bài 8 trang 39 Chuyên đề Toán 10: Từ 15 bút chì màu có màu khác nhau đôi một,
a) Có bao nhiêu cách chọn ra một số bút chì màu, tính cả trường hợp không chọn cái nào?
b) Có bao nhiêu cách chọn ra ít nhất 8 bút chì màu?
Lời giải:
a) Có cách chọn ra 0 bút chì màu;
Có cách chọn ra 1 bút chì màu;
Có cách chọn ra 2 bút chì màu;
...
Có cách chọn ra 15 bút chì màu.
Vậy có tổng cộng cách chọn ra một số bút chì màu.
b) Số cách chọn ra ít nhất 8 bút chì màu là:
Vì:
nên:
Vậy có 22819 cách chọn ra ít nhất 8 bút chì màu.
Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 10 (hay nhất) – Chân trời sáng tạo
- Tác giả tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Soạn văn lớp 10 (ngắn nhất) – Chân trời sáng tạo
- Tóm tắt tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Giải sbt Ngữ văn lớp 10 – Chân trời sáng tạo
- Bố cục tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Nội dung chính tác phẩm Ngữ văn lớp 10 – Chân trời sáng tạo
- Văn mẫu lớp 10 – Chân trời sáng tạo
- Giải Chuyên đề học tập Ngữ văn 10 – Chân trời sáng tạo
- Giải sgk Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Giải sbt Tiếng Anh 10 Friends Global – Chân trời sáng tạo
- Trọn bộ Từ vựng Tiếng Anh 10 Friends Global đầy đủ nhất
- Ngữ pháp Tiếng Anh 10 Friends Global
- Giải sgk Vật lí 10 – Chân trời sáng tạo
- Giải sbt Vật lí 10 – Chân trời sáng tạo
- Lý thuyết Vật lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Vật lí 10 – Chân trời sáng tạo
- Giải sgk Hóa học 10 – Chân trời sáng tạo
- Lý thuyết Hóa học 10 – Chân trời sáng tạo
- Giải sbt Hóa học 10 – Chân trời sáng tạo
- Giải Chuyên đề Hóa học 10 – Chân trời sáng tạo
- Giải sgk Sinh học 10 – Chân trời sáng tạo
- Giải sbt Sinh học 10 – Chân trời sáng tạo
- Lý thuyết Sinh học 10 – Chân trời sáng tạo
- Giải Chuyên đề Sinh học 10 – Chân trời sáng tạo
- Giải sgk Lịch sử 10 – Chân trời sáng tạo
- Giải sbt Lịch sử 10 – Chân trời sáng tạo
- Giải Chuyên đề Lịch sử 10 – Chân trời sáng tạo
- Lý thuyết Lịch sử 10 – Chân trời sáng tạo
- Giải sgk Địa lí 10 – Chân trời sáng tạo
- Lý thuyết Địa Lí 10 - Chân trời sáng tạo
- Giải sbt Địa lí 10 – Chân trời sáng tạo
- Giải Chuyên đề Địa lí 10 – Chân trời sáng tạo
- Giải sgk Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải sbt Giáo dục Kinh tế và Pháp luật 10 – Chân trời sáng tạo
- Giải Chuyên đề Kinh tế và pháp luật 10 – Chân trời sáng tạo
- Lý thuyết KTPL 10 – Chân trời sáng tạo
- Giải sgk Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sbt Hoạt động trải nghiệm 10 – Chân trời sáng tạo
- Giải sgk Giáo dục thể chất 10 – Chân trời sáng tạo
