Nội dung bài viết

    Xem thêm

    Giải bài tập trang 34, 35 Chuyên đề Toán 10 Bài 2 - Chân trời sáng tạo

    Với Giải bài tập trang 34, 35 Chuyên đề Toán 10 trong Bài 2: Nhị thức Newton sách Chuyên đề Toán lớp 10 Chân trời sáng tạo  hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Chuyên đề Toán 10 trang 34, 35.

    1 1,803 20/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải bài tập trang 34, 35 Chuyên đề Toán 10 Bài 2 - Chân trời sáng tạo

    Khám phá 1 trang 34 Chuyên đề Toán 10: Có ba hộp, mỗi hộp đựng hai quả cầu được dán nhãn a và b (xem Hình 1).

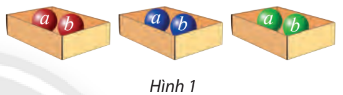
    Chuyên đề Toán 10 Bài 2: Nhị thức Newton - Chân trời sáng tạo (ảnh 1)

    Lấy từ mỗi hộp một quả cầu. Có bao nhiêu cách lấy để trong ba quả cầu lấy ra:

    a) có 3 quả cầu dán nhãn b?

    b) có 2 quả cầu dán nhãn b?

    c) có 1 quả cầu dán nhãn b?

    d) không có quả cầu nào dán nhãn b?

    Lời giải:

    a) Vì có tổng cộng 3 quả cầu dán nhãn b nên có C33 = 1 cách lấy ra 3 quả cầu dán nhãn b.

    b) Vì có tổng cộng 3 quả cầu dán nhãn b nên có C32 = 3 cách lấy ra 2 quả cầu dán nhãn b.

    c) Vì có tổng cộng 3 quả cầu dán nhãn b nên có C31 = 3 cách lấy ra 1 quả cầu dán nhãn b.

    d) Vì có tổng cộng 3 quả cầu dán nhãn b nên có C30 = 1 cách lấy ra 1 quả cầu dán nhãn b.

    Thực hành 1 trang 35 Chuyên đề Toán 10: Hãy khai triển:

    a) (x – y)6;

    b) (1 + x)7.

    Lời giải:

    a) (x – y)6

    =C60x6+C61x5−y+C62x4−y2+C63x3−y3+C64x2−y4+C65x−y5+C66−y6

    =x6−C61x5y+C62x4y2−C63x3y3+C64x2y4−C65xy5+y6

    =x6−6x5y+15x4y2−20x3y3+15x2y4−6xy5+y6.

    b) (1 + x)7

    =C7017+C7116x+C7215x2+C7314x3+C7413x4+C7512x5+C761x6+C77x7

    = 1 + 7x + 21x2 + 35x3 + 35x4 + 21x5 + 7x6 + x7.

    Khám phá 2 trang 35 Chuyên đề Toán 10: Từ các công thức khai triển:

    (a + b)0 = 1;

    (a + b)1 = a + b;

    (a + b)2 = a2 + 2ab + b2;

    (a + b)3 = a3 + 3a2b + 3ab2 + b3;

    (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4;

    (a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5;

    các hệ số được viết thành bảng số như Hình 2 sau đây. Nếu sử dụng kí hiệu tổ hợp thì nhận được bảng như Hình 3.

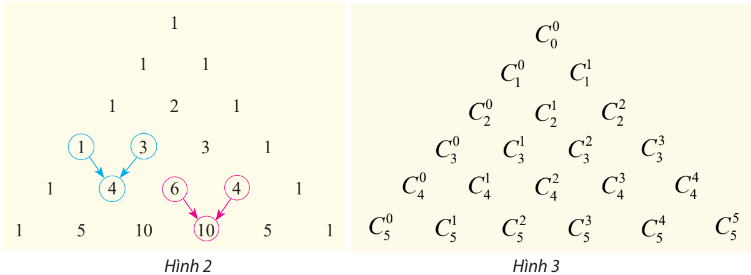
    Chuyên đề Toán 10 Bài 2: Nhị thức Newton - Chân trời sáng tạo (ảnh 1)

    Từ các đẳng thức như

    C30=C33=1,C41=C43=4,C30+C31=C41,C42+C43=C53,

    có thể dự đoán rằng, với mỗi n∈ℕ*,

    Cnk=Cnn−k   (0≤k≤n);

    Cnk−1+Cnk=Cn+1k   (1≤k≤n).

    Hãy chứng minh các công thức trên.

    Gợi ý: Sử dụng công thức Cnk=n!k!(n−k)!,n∈ℕ,0≤k≤n.

    Lời giải:

    +) Có

    Cnk=n!k!(n−k)!,  Cnn−k=n!(n−k)!n−n−k!=n!(n−k)!k!=n!k!(n−k)!.

    Vậy Cnk=Cnn−k.

    +) Cnk−1+Cnk=n!k−1!n−k+1!+n!k!n−k!

    =n+1!n+1k!kn−k+1!+n+1!n+1k!n−k+1!n−k+1=kn+1.n+1!k!n−k+1!+n−k+1n+1.n+1!k!n−k+1!

    =kn+1.n+1!k!n+1−k!+n−k+1n+1.n+1!k!n+1−k!

    =kn+1.Cn+1k+n−k+1n+1.Cn+1k=kn+1+n−k+1n+1Cn+1k

    =k+n−k+1n+1Cn+1k=n+1n+1Cn+1k=Cn+1k.

    Xem thêm lời giải bài tập Chuyên đề Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

    Giải bài tập trang 37, 38 Chuyên đề Toán 10 Bài 2

    Giải bài tập trang 39 Chuyên đề Toán 10 Bài 2

    Tham khảo các loạt bài Toán 10 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,803 20/07/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: