Câu hỏi:
21/07/2024 107Xét khối tứ diện ABCD có cạnh AD=x và các cạnh còn lại đều bằng 2. Tìm x để thể tích khối tứ diện ABCD đạt giá trị lớn nhất.
A. x=2√3
B. x=√6
Đáp án chính xác
C. x=2
D. x=√3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Đặt a=2. Gọi H là trung điểm của BC khi đó {AH⊥BCDH⊥BC
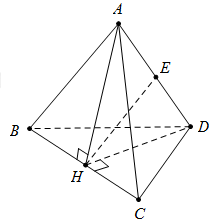
Suy ra BC⊥(AHD)và ta có AH=DH=a√32
Gọi E là trung điểm của AD do tam giác AHD cân nên
HE⊥AD⇒HE=√AH2−AE2=√3a24−x24
Ta có VABCD=VB.AHD+VC.AHD
=13BC.SAHD=13a.12HE.AD
Lại có:
√3a24−x24.x=2√3a24−x24.x2≤(3a24−x24+x24)
=3a24⇒VABCD≤a38⇒Vmax=a38.
Dấu bằng xảy ra 3a2=2x2⇔x=a√62=√6
Cách 2: Nhận xét Vmax⇔SAHD lớn nhất 12AH.DHsin
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 13:
Đồ thị hàm số cắt đồ thị hàm số tại hai điểm phân biệt A và B. Khi đó độ dài đoạn AB là
Xem đáp án »
14/07/2024
130



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)