Câu hỏi:
17/07/2024 78
Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau?
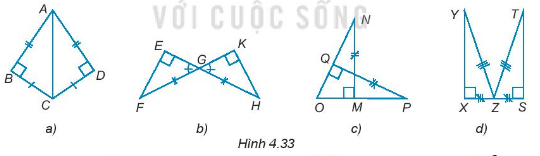
Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau?

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
+) Hình a:
Xét ∆ABC và ∆ADC ta có:
AB = AD (giả thiết)
\(\widehat {ABC}\) = \(\widehat {ADC}\) = 90° (giả thiết)
BC = CD (giả thiết)
Do đó, ∆ABC = ∆ADC (hai cạnh góc vuông).
+) Hình b
Xét ∆EFG và ∆KHG ta có:
GF = GH (giả thiết)
\(\widehat {FEG}\) = \(\widehat {HKG}\) = 90° (giả thiết)
\(\widehat {EGF}\) = \(\widehat {HGK}\) (hai góc đối đỉnh)
Do đó, ∆EFG = KHG (góc nhọn – cạnh huyền)
+) Hình c:
Tam giác OMN vuông tại M nên \(\widehat {ONM} + \widehat O = 90^\circ \Rightarrow \widehat {ONM} = 90^\circ - \widehat O\).
Tam giác OQP vuông tại Q nên \(\widehat {OPQ} + \widehat O = 90^\circ \Rightarrow \widehat {OPQ} = 90^\circ - \widehat O\).
Do đó, \(\widehat {ONM} = \widehat {OPQ}\).
Xét ∆OMN và ∆OQP ta có:
MN = PQ (giả thiết)
\(\widehat {OMN}\) = \(\widehat {OQP}\) = 90o (giả thiết)
\(\widehat {ONM} = \widehat {OPQ}\) (chứng minh trên)
Do đó, ∆OMN = ∆OQP (góc nhọn – cạnh góc vuông).
+) Hình d:
Xét ∆XYZ và ∆STZ ta có:
YZ = TZ (giả thiết)
\(\widehat {YXZ}\) = \(\widehat {TSZ}\) = 90° (giả thiết)
XZ = SZ (giả thiết)
Do đó, ∆XYZ = ∆STZ (cạnh huyền – cạnh góc vuông).
Hướng dẫn giải
+) Hình a:
Xét ∆ABC và ∆ADC ta có:
AB = AD (giả thiết)
\(\widehat {ABC}\) = \(\widehat {ADC}\) = 90° (giả thiết)
BC = CD (giả thiết)
Do đó, ∆ABC = ∆ADC (hai cạnh góc vuông).
+) Hình b
Xét ∆EFG và ∆KHG ta có:
GF = GH (giả thiết)
\(\widehat {FEG}\) = \(\widehat {HKG}\) = 90° (giả thiết)
\(\widehat {EGF}\) = \(\widehat {HGK}\) (hai góc đối đỉnh)
Do đó, ∆EFG = KHG (góc nhọn – cạnh huyền)
+) Hình c:
Tam giác OMN vuông tại M nên \(\widehat {ONM} + \widehat O = 90^\circ \Rightarrow \widehat {ONM} = 90^\circ - \widehat O\).
Tam giác OQP vuông tại Q nên \(\widehat {OPQ} + \widehat O = 90^\circ \Rightarrow \widehat {OPQ} = 90^\circ - \widehat O\).
Do đó, \(\widehat {ONM} = \widehat {OPQ}\).
Xét ∆OMN và ∆OQP ta có:
MN = PQ (giả thiết)
\(\widehat {OMN}\) = \(\widehat {OQP}\) = 90o (giả thiết)
\(\widehat {ONM} = \widehat {OPQ}\) (chứng minh trên)
Do đó, ∆OMN = ∆OQP (góc nhọn – cạnh góc vuông).
+) Hình d:
Xét ∆XYZ và ∆STZ ta có:
YZ = TZ (giả thiết)
\(\widehat {YXZ}\) = \(\widehat {TSZ}\) = 90° (giả thiết)
XZ = SZ (giả thiết)
Do đó, ∆XYZ = ∆STZ (cạnh huyền – cạnh góc vuông).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF = CE.
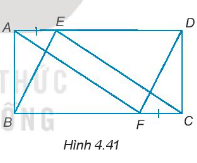
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF = CE.

Câu 2:
Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng \(\widehat {DAB} = \widehat {CAB}\), hãy chứng minh CB = DB.
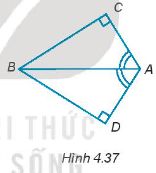
Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng \(\widehat {DAB} = \widehat {CAB}\), hãy chứng minh CB = DB.

Câu 3:
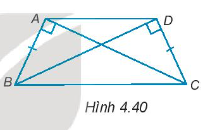
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AD // BC.
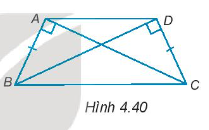
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AD // BC.

Câu 4:
Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED.
Chứng minh rằng:
∆AED = ∆BEC.
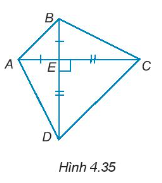
Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED.
Chứng minh rằng:
∆AED = ∆BEC.

Câu 5:
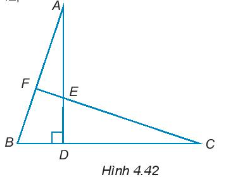
Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
Chứng minh rằng AB = CE.
Câu 6:
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.
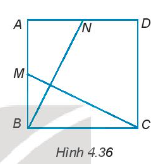
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.

Câu 7:
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AC = BD.
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AC = BD.

Câu 8:
Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
Cho đường thẳng CE cắt AB tại F. Chứng minh rằng \(\widehat {BFC} = 90^\circ \).
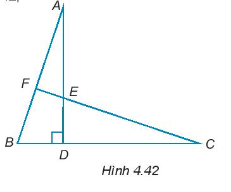
Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
Cho đường thẳng CE cắt AB tại F. Chứng minh rằng \(\widehat {BFC} = 90^\circ \).

Câu 9:
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF // CE.
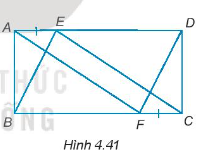
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF // CE.

Câu 10:
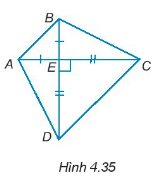
Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED.
Chứng minh rằng:
∆ABC = ∆BAD.
Câu 11:
Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh rằng ∆ABE = ∆DCE.
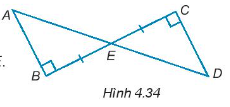
Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh rằng ∆ABE = ∆DCE.

Câu 12:
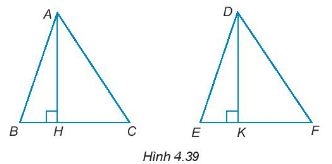
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
Nếu AB = DE, AC = DF và AH = DK thì ∆ABC = ∆DEF.
Câu 13:
Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng ∆ABC = ∆DEF, hãy chứng minh AH = DK.
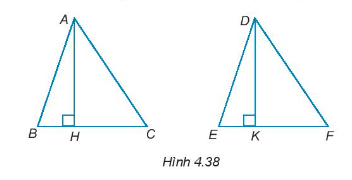
Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng ∆ABC = ∆DEF, hãy chứng minh AH = DK.

Câu 14:
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
Nếu AB = DE; BC = EF và AH = DK thì ∆ABC = ∆DEF;
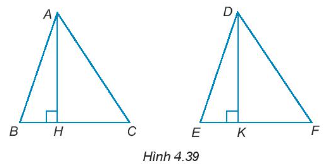
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
Nếu AB = DE; BC = EF và AH = DK thì ∆ABC = ∆DEF;



