Câu hỏi:
18/07/2024 120
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.
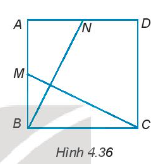
Cho hình vuông ABCD. Gọi M và N lần lượt là trung điểm của AB và AD (H.4.36). Chứng minh rằng BN = CM và BN ⊥ CM.

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Vì ABCD là hình vuông nên AB = BC = CD = DA.
Vì N là trung điểm của AD nên AN = ND = \(\frac{{AD}}{2}\).
Vì M là trung điểm của AB nên AM = MB = \(\frac{{AB}}{2}\).
Mà AB = AD nên AN = BM.
Xét ∆ANB và ∆BMC có:
AN = BM (chứng minh trên)
AB = BC (chứng minh trên)
\(\widehat {NAB}\) = \(\widehat {MBC}\) = 90° (do ABCD là hình vuông)
Do đó, ∆ANB = ∆BMC (hai cạnh góc vuông)
Suy ra, BN = CM (hai cạnh tương ứng).
Gọi E là giao điểm của BN và CM.
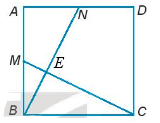
Do ∆ANB = ∆BMC nên \(\widehat {EMB} = \widehat {CMB} = \widehat {BNA}\).
Từ định lí tổng ba góc trong tam giác BME và tam giác ABN, ta suy ra:
\(\widehat {BEM} = 180^\circ - \widehat {EMB} - \widehat {MBE} = 180^\circ - \widehat {BNA} - \widehat {ABN} = \widehat {BAN} = 90^\circ \).
Vậy BN vuông góc với CM tại E.
Hướng dẫn giải
Vì ABCD là hình vuông nên AB = BC = CD = DA.
Vì N là trung điểm của AD nên AN = ND = \(\frac{{AD}}{2}\).
Vì M là trung điểm của AB nên AM = MB = \(\frac{{AB}}{2}\).
Mà AB = AD nên AN = BM.
Xét ∆ANB và ∆BMC có:
AN = BM (chứng minh trên)
AB = BC (chứng minh trên)
\(\widehat {NAB}\) = \(\widehat {MBC}\) = 90° (do ABCD là hình vuông)
Do đó, ∆ANB = ∆BMC (hai cạnh góc vuông)
Suy ra, BN = CM (hai cạnh tương ứng).
Gọi E là giao điểm của BN và CM.

Do ∆ANB = ∆BMC nên \(\widehat {EMB} = \widehat {CMB} = \widehat {BNA}\).
Từ định lí tổng ba góc trong tam giác BME và tam giác ABN, ta suy ra:
\(\widehat {BEM} = 180^\circ - \widehat {EMB} - \widehat {MBE} = 180^\circ - \widehat {BNA} - \widehat {ABN} = \widehat {BAN} = 90^\circ \).
Vậy BN vuông góc với CM tại E.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
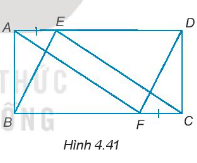
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF = CE.
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF = CE.

Câu 2:
Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng \(\widehat {DAB} = \widehat {CAB}\), hãy chứng minh CB = DB.
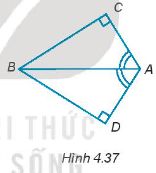
Cho bốn điểm A, B, C, D như Hình 4.37. Biết rằng \(\widehat {DAB} = \widehat {CAB}\), hãy chứng minh CB = DB.

Câu 3:
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AD // BC.
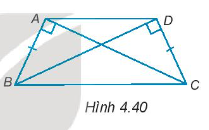
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AD // BC.

Câu 4:
Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED.
Chứng minh rằng:
∆AED = ∆BEC.
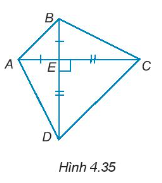
Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED.
Chứng minh rằng:
∆AED = ∆BEC.

Câu 5:
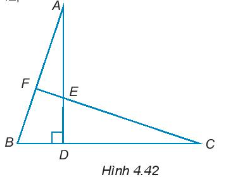
Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
Chứng minh rằng AB = CE.
Câu 6:
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AC = BD.
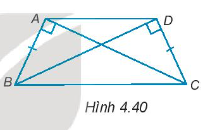
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC. Chứng minh rằng:
AC = BD.

Câu 7:
Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
Cho đường thẳng CE cắt AB tại F. Chứng minh rằng \(\widehat {BFC} = 90^\circ \).
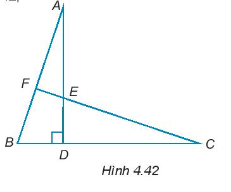
Cho năm điểm A, B, C, D, E như Hình 4.42, trong đó DA = DC, DB = DE.
Cho đường thẳng CE cắt AB tại F. Chứng minh rằng \(\widehat {BFC} = 90^\circ \).

Câu 8:
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF // CE.
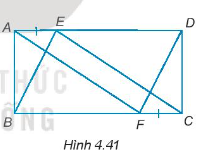
Cho hình chữ nhật ABCD. Trên cạnh AD và BC lần lượt lấy hai điểm E và F sao cho AE = CF (H.4.41). Chứng minh rằng:
AF // CE.

Câu 9:
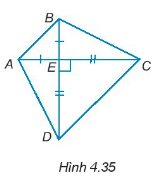
Cho các điểm A, B, C, D, E như Hình 4.35. Biết rằng AC vuông góc với BD, EA = EB và EC = ED.
Chứng minh rằng:
∆ABC = ∆BAD.
Câu 10:
Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh rằng ∆ABE = ∆DCE.
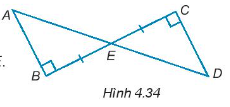
Cho các điểm A, B, C, D, E như Hình 4.34. Biết rằng E là trung điểm của BC, chứng minh rằng ∆ABE = ∆DCE.

Câu 11:
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
Nếu AB = DE, AC = DF và AH = DK thì ∆ABC = ∆DEF.
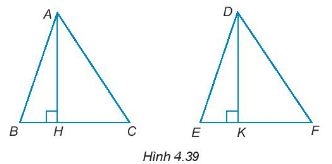
Câu 12:
Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng ∆ABC = ∆DEF, hãy chứng minh AH = DK.
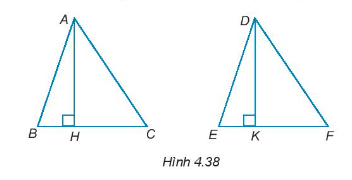
Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng ∆ABC = ∆DEF, hãy chứng minh AH = DK.

Câu 13:
Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau?
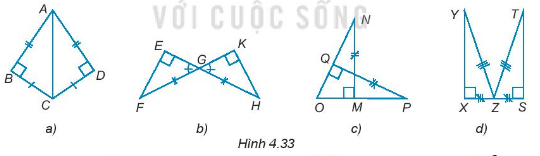
Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau?

Câu 14:
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
Nếu AB = DE; BC = EF và AH = DK thì ∆ABC = ∆DEF;
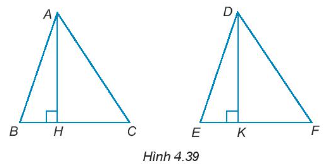
Cho AH và DK lần lượt là hai đường cao của tam giác ABC và DEF như Hình 4.39. Chứng minh rằng:
Nếu AB = DE; BC = EF và AH = DK thì ∆ABC = ∆DEF;



