Câu hỏi:
12/07/2024 143Trong không gian Oxyz cho mặt cầu và mặt phẳng . Gọi M là một điểm bất kì trên mặt cầu (S). Khoảng cách từ M đến (P) có giá trị nhỏ nhất bằng
A.
B.
C. 0
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Mặt cầu (S) có tâm I(1;-2;2) và bán kính R = 2.
Dễ thấy nên (P) và (S) không cắt nhau.
Gọi M' là giao điểm của đường thằng qua I và vuông góc với (P) như hình vẽ.
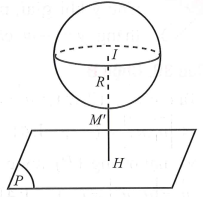
Ta thấy nên đạt GTNN bằng khi .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho các điểm A(1;4;5), B(0;3;1), C(2;-1;0) và mặt phẳng (P): 3x - 3y - 2z - 15 = 0. Gọi M(a;b;c) là điểm thuộc (P) sao cho tổng các bình phương khoảng cách từ M đến A, B, C nhỏ nhất. Tính a + b + c.
Câu 2:
Cho hàm số y = f(x) có bảng biến thiên như sau
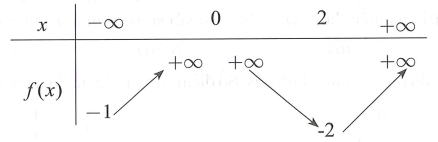
Tập hợp tất cả các giá trị thực của tham số m để phương trình f(x) + m = 0 có hai nghiệm phân biệt là
Câu 3:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;10] để hàm số nghịch biến trên khoảng (1;2)?
Câu 4:
Cho hàm số có đồ thị như hình dưới đây. Số điểm cực trị của đồ thị hàm số là
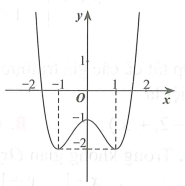
Câu 6:
Cho hình chóp S.ABC có đường cao SA, tam giác ABC vuông tại A có AB = 2, AC = 4. Gọi H là trung điểm của BC. Biết diện tích tam giác SAH bằng 2, thể tích của khối chóp S.ABC bằng
Câu 8:
Biết số phức z = -3 + 4i là một nghiệm của phương trình , trong đó a, b là các số thực. Tính a - b.
Câu 9:
Cho hàm số y = f(x) có đồ thị như hình dưới đây. Diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục Ox là:
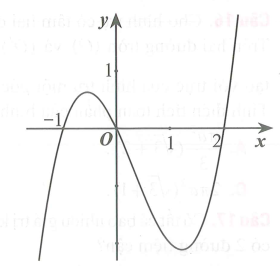
Câu 10:
Thể tích của khối trụ tròn xoay có bán kính đáy và chiều cao đều bằng 5 là:
Câu 11:
Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác cân tại A có Biết thể tích khối chóp S.ABC bằng góc giữa hai mặt phẳng (SBC) và (ABC) bằng
Câu 13:
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Biết SA = 3, SB = 4, SC = 5 thể tích khối chóp S.ABC bằng
Câu 14:
Trong không gian Oxyz, khoảng cách từ gốc tọa độ (O) đến mặt phẳng (P): x - y + 2z = 0 bằng
Câu 15:
Trong không gian Oxyz, hình chiếu của điểm M(1;2;3) trên mặt phẳng (Oxy) có tọa độ là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)