Câu hỏi:
19/07/2024 192Trên cánh đồng có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa hai cọc là 4 mét, còn 2 sợi dây cột 2 con bò dài 3 mét và 2 mét. Tính phần diện tích mặt cỏ lớn nhất mà 2 con bò có thể ăn chung (lấy giá trị gần đúng nhất).
A. 1,989m2
B. 1,034m2
C. 1,574m2
D. 2,824m2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Con bò thứ nhất có thể ăn cỏ trong hình tròn tâm A bán kính AC=3m.
Con bò thứ hai có thể ăn cỏ trong hình tròn tâm B bán kính BC=2m.
Phần diện tích lớn nhất hai con có thể ăn chung là phần giao của hai hình tròn (phần gạch sọc).
Xét tam giác ABC có AC=3;BC=2;AB=4.
⇒cos^ABC=BA2+BC2−AC22BA.BC=1116
⇒^ABC≈46°
Lại có và
Vậy
|
Nhận xét: mỗi con bò có thể ăn cỏ trong hình tròn có tâm là cọc buộc, bán kính là dây buộc. Do đó phần diện tích cỏ có thể ăn chung lớn nhất chính là phần giao nhau của hai hình tròn. |
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Thể tích V của khối hộp chữ nhật ABCD.A'B'C'D' biết AB = a; AD = 2a; là
Câu 2:
Một thùng rượu có bán kính đáy là thiết diện vuông góc với trục và cách đều hai đáy có bán kính là 40 cm, chiều cao thùng rượu là 1m (hình vẽ). Biết rằng mặt phẳng chứa trục và cắt mặt xung quanh thùng rượu là các đường parabol, hỏi thể tích của thùng rượu (đơn vị lít) là bao nhiêu?

Câu 3:
Trong mặt phẳng tọa độ Oxy, cho điểm M, N, P lần lượt là điểm biểu diễn của các số phức . Tọa độ điểm Q sao cho tứ giác MNPQ là hình bình hành là
Câu 4:
Cho hình lập phương ABCD.A'B'C'D'; cạnh bằng a. Gọi O là giao điểm của AC và BD. Thể tích của tứ diện OA'BC bằng
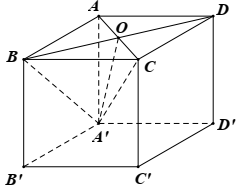
Câu 5:
Trong không gian với hệ tọa độ Oxyz, cho M(1;2;3), N(2;-3;1), P(3;1;2). Tìm tọa độ điểm Q sao cho MNPQ là hình bình hành
Câu 6:
Trong không gian hệ tọa độ Oxyz, cho điểm A(1;a;1) và mặt cầu (S) có phương trình . Tập các giá trị của a để điểm A nằm trong khối cầu là
Câu 7:
Trong không gian với hệ tọa độ Oxyz. Phương trình mặt phẳng đi qua 3 điểm A(-3;0;0), B(0;4;0), C(0;0;-2) là
Câu 8:
Cho hai điểm A, B là hai điểm biểu diễn hình học số phức theo thứ tự khác 0 và thỏa mãn đẳng thức . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ). Chọn phương án đúng và đầy đủ nhất.
Câu 9:
Cho lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Thể tích của khối cầu đi qua các đỉnh của lăng trụ bằng
Câu 10:
Cho khối chóp S.ABC có SA = SB = SC = a, . Gọi M, N lần lượt là các điểm trên cạnh AB và SC sao cho . Khi khoảng cách giữa M và N nhỏ nhất, tính thể tích V của khối chóp S.AMN
Câu 11:
Cho tứ diện ABCD có , các tam giác ABC, ACD, ABD là các tam giác vuông tại đỉnh A. Khoảng cách d từ điểm A đến mặt phẳng (BCD) là
Câu 12:
Trong không gian với hệ trục tọa độ Oxyz cho ba mặt phẳng ; . Một đường thẳng d thay đổi cắt ba mặt lần lượt tại A, B, C. Tìm giá trị nhỏ nhất của .
Câu 13:
Biết rằng đường thẳng y = 2x - 3 cắt đồ thị hàm số tại hai điểm phân biệt A và B, biết điểm B có hoành độ âm. Hoành độ của điểm B bằng
Câu 14:
Cho số thực x thỏa mãn (a, b, c là các số thực dương). Hãy biểu diễn x theo a, b, c.
Câu 15:
Cho số phức z = 2 - 3i. Điểm biểu diễn số phức liên hợp của z là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)