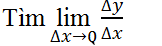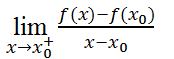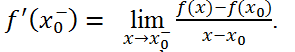Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
* Lời giải:
y'
* Phương pháp giải:
Nắm vững bảng quy tắc đạo hàm

* Lý thuyết nắm thêm:
1. Định nghĩa đạo hàm
Giới hạn nếu có của tỉ số giữa số gia của hàm số và số gia của đối số tại , khi số gia của đối số tiến dần tới 0, được gọi là đạo hàm của hàm số
tại điểm
.
Cho hàm số xác định trên
và
:
=
=
Nếu hàm số có đạo hàm tại
thì nó liên tục tại điểm đó.
2. Cách tính đạo hàm bằng định nghĩa
Quy tắc tính đạo hàm bằng định nghĩa:
+ Bước 1: Giả sử ∆x là số gia của đối số tại x0; tính :
∆y= f( x0+ ∆x)- f( x0) .
+ Bước 2: Lập tỉ số ∆y/∆x.
+ Bước 3:
3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số
* Định lí: Nếu hàm số y= f( x) có đạo hàm tại x0 thì nó liên tục tại điểm đó.
* Chú ý:
+ Nếu hàm số y= f(x) gián đoạn tại x0 thì hàm số không có đạo hàm tại điểm đó.
+ Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.
4. Đạo hàm một bên, Đạo hàm trên khoảng, trên đoạn
a. Đạo hàm bên trái, bên phải
+ Nếu tồn tại giới hạn( hữu hạn) bên phải
ta gọi giới hạn đó là đạo hàm bên phải của hàm số y= f(x) tại x=x0 và kí hiệu f'(x0+)
+ Tương tự; đạo hàm bên trái của hàm số là
Hệ quả : Hàm số y= f(x) có đạo hàm tại x0 khi và chỉ khi tồn tại f'(x0+) và f;(x0-) đồng thời f' (x0+ )=f'(x0-) .
b. Đạo hàm trên khoảng, trên đoạn
Hàm số y=f(x) có đạo hàm trên (a;b) nếu nó có đạo hàm tại mọi điểm thuộc (a; b).
Hàm số y= f(x) có đạo hàm trên[a;b] nếu nó có đạo hàm tại mọi điểm thuộc khoảng (a; b) đồng thời tồn tại đạo hàm trái tại x= b và đạo hàm phải tại x= a.
5. Ý nghĩa hình học của đạo hàm
Định lí: Đạo hàm của hàm số y= f(x) taị điểm x=x0 là hệ số góc của tiếp tuyến M0T của đồ thị hàm số y= f( x) tại điểm M0(x0; f(x0)).
Định lí: Phương trình tiếp tuyến của đồ thị hàm số y= f(x) tại điểm M0(x0; f(x0)) là:
y – y0= f’(x0) ( x- x0)
trong đó y0= f( x0)
Xem thêm các bài viết liên quan hay, chi tiết:
Quy tắc tính đạo hàm và cách giải các dạng bài tập (2024) chi tiết nhất
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Một amino axit có công thức phân tử C4H9NO2. Số đồng phân amino axit là
Câu 5:
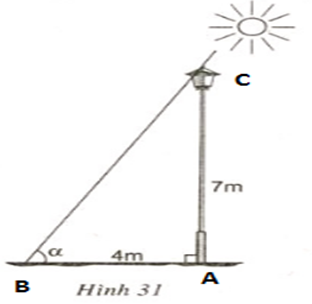
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc α trong hình 31)
Câu 6:
Hai ô tô A và B chạy cùng chiều trên cùng một đoạn đường với vận tốc 70 km/giờ và 65 km/giờ. Vận tốc của ô tô A so với ô tô B bằng
Câu 7:
Có 32 khách du lịch đi thuyền tham quan. Mỗi chiếc thuyền chở được 5 hành khách. Hỏi cần ít nhất mấy chiếc thuyền để chở hết số khách du lịch đó?
Câu 9:
Một mảnh vườn hình chữ nhật có chu vi bằng 104 m, chiều dài bằng chiều rộng. Người ta trồng rau trên mảnh vườn đó. Trung bình cứ 1 m2 thu hoạch được 5 kg rau. Tính:
a) Diện tích của mảnh vườn đó.
b) Số ki-lô-gam rau thu hoạch được trên cả mảnh vườn đó.
Câu 10:
Cho hình trụ có bán kính đáy R = 8 và độ dài đường sinh l = 3. Diện tích xung quanh của hình trụ đã cho bằng:
Câu 11:
Cho hàm số . Tìm tất cả các giá trị thực của tham số để hàm số đã cho nghịch biến trên ?
Câu 12:
Cắt hình nón đỉnh S bởi mặt phẳng đi qua trục ta được một tam giác vuông cân, cạnh huyền bằng . Thể tích khối nón là:
Câu 14:
Cho phương trình log2(2x-1)2 = 2log2(x-2). Số nghiệm thực của phương trình là: