Câu hỏi:
19/11/2024 122
Thể tích khối lập phương cạnh 2 bằng
Thể tích khối lập phương cạnh 2 bằng
A. 6
B. 8
C. 4
D. 2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: B.
*Lời giải:
Thể tích khối lập phương là
*Phương pháp giải:
- Nắm vững lại kiến thức về hình lập phương: định nghĩa, tính chất, công thức tính S và V
- Thể tích hình lập phương: V = a.a.a =
*Một số lý thuyết và dạng bài tập về hình lập phương:
Hình lập phương là hình hộp chữ nhật có 6 mặt đều là những hình vuông.
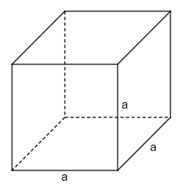
- Thể tích hình lập phương: V = a.a.a =
- Diện tích mỗi mặt của hình lập phương là S = a2
- Diện tích toàn phần (tổng diện tích các mặt) của hình lập phương là Stp = 6a2
- Độ dài đường chéo của hình lập phương là d =
- Độ dài đường chéo mỗi mặt của hình lập phương là
- d(A, (A'BD)) =
- d(A, (CB'D')) =
- d (AC', CD) = d(AC', A'B') =
HÌNH HỘP CHỮ NHẬT
1. Định nghĩa
Hình hộp chữ nhật là một hình không gian có 6 mặt đều là hình chữ nhật.
Hai mặt đối diện nhau của hình chữ nhật được xem là hai mặt đáy của hình chữ nhật. Các mặt còn lại đều là mặt bên của hình chữ nhật.
Hình hộp chữ nhật ba chiều: chiều dài, chiều rộng, chiều cao
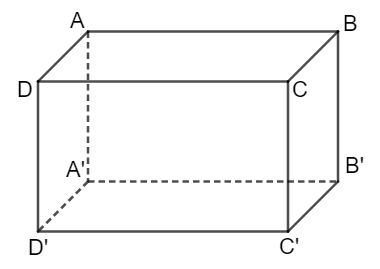
Hình hộp chữ nhật có:
+ 12 cạnh: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’
+ 8 đỉnh: đỉnh A, đỉnh B, đỉnh C, đỉnh D, đỉnh A’, đỉnh B’, đỉnh C, đỉnh D’
+ 6 mặt: ABCD, BCC’B’, A’B’C’D’, DCD’C’, ADD’C’, ABB’A’.
2. Công thức
Cho hình vẽ:
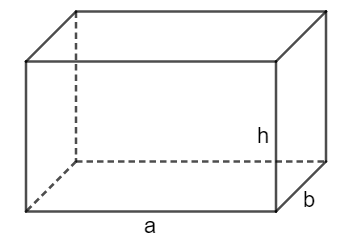
Trong đó:
a: Chiều dài
b: Chiều rộng
h: Chiều cao
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hình hộp chữ nhật. Hình lập phương (mới 2024 + Bài Tập) - Toán lớp 5
Công thức tính thể tích hình lập phương (chính xác nhất) và cách giải các dạng bài tập
Đáp án đúng: B.
*Lời giải:
Thể tích khối lập phương là
*Phương pháp giải:
- Nắm vững lại kiến thức về hình lập phương: định nghĩa, tính chất, công thức tính S và V
- Thể tích hình lập phương: V = a.a.a =
*Một số lý thuyết và dạng bài tập về hình lập phương:
Hình lập phương là hình hộp chữ nhật có 6 mặt đều là những hình vuông.

- Thể tích hình lập phương: V = a.a.a =
- Diện tích mỗi mặt của hình lập phương là S = a2
- Diện tích toàn phần (tổng diện tích các mặt) của hình lập phương là Stp = 6a2
- Độ dài đường chéo của hình lập phương là d =
- Độ dài đường chéo mỗi mặt của hình lập phương là
- d(A, (A'BD)) =
- d(A, (CB'D')) =
- d (AC', CD) = d(AC', A'B') =
HÌNH HỘP CHỮ NHẬT
1. Định nghĩa
Hình hộp chữ nhật là một hình không gian có 6 mặt đều là hình chữ nhật.
Hai mặt đối diện nhau của hình chữ nhật được xem là hai mặt đáy của hình chữ nhật. Các mặt còn lại đều là mặt bên của hình chữ nhật.
Hình hộp chữ nhật ba chiều: chiều dài, chiều rộng, chiều cao

Hình hộp chữ nhật có:
+ 12 cạnh: AB, BC, CD, DA, A’B’, B’C’, C’D’, D’A’, AA’, BB’, CC’, DD’
+ 8 đỉnh: đỉnh A, đỉnh B, đỉnh C, đỉnh D, đỉnh A’, đỉnh B’, đỉnh C, đỉnh D’
+ 6 mặt: ABCD, BCC’B’, A’B’C’D’, DCD’C’, ADD’C’, ABB’A’.
2. Công thức
Cho hình vẽ:

Trong đó:
a: Chiều dài
b: Chiều rộng
h: Chiều cao
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Hình hộp chữ nhật. Hình lập phương (mới 2024 + Bài Tập) - Toán lớp 5
Công thức tính thể tích hình lập phương (chính xác nhất) và cách giải các dạng bài tập
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
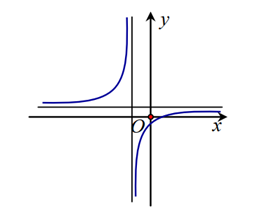
Cho hàm số có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?

Câu 2:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 2] để hàm số đồng biến trên .
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 2] để hàm số đồng biến trên .
Câu 3:
Người ta cần đổ một ống cống thoát nước hình trụ với chiều cao 2m, độ dày thành ống là 10cm. Đường kính ống là 50cm. Tính lượng bê tông cần dùng để làm ra ống thoát nước đó?
Người ta cần đổ một ống cống thoát nước hình trụ với chiều cao 2m, độ dày thành ống là 10cm. Đường kính ống là 50cm. Tính lượng bê tông cần dùng để làm ra ống thoát nước đó?
Câu 4:
Một khối đồ chơi bằng gỗ có các hình chiếu đứng, hình chiếu cạnh và hình chiếu bằng như hình bên (các kích thước cho như trong hình).
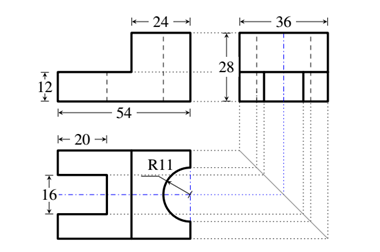
Tính thể tích của khối đồ chơi đó (làm tròn kết quả đến chữ số hàng đơn vị).
Câu 5:
Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b]. Khẳng định nào sau đây là khẳng định đúng?
Cho f(x) là hàm số liên tục trên đoạn [a; b]. Giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b]. Khẳng định nào sau đây là khẳng định đúng?
Câu 7:
Tập trình nghiệm của bất phương trình có dạng Tính giá trị biểu thức M = a + b
Câu 8:
Xét các số phức z thỏa mãn là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả các điểm biểu diễn số phức z là một đường tròn có bán kính bằng
Câu 9:
Cho hình phẳng (H) giới hạn bởi đồ thị và trục hoành. Tính thể tích V vật thể tròn xoay sinh ra khi cho (H) quay quanh Ox.
Câu 12:
Cho hàm số y = f(x) có đồ thị như hình bên:
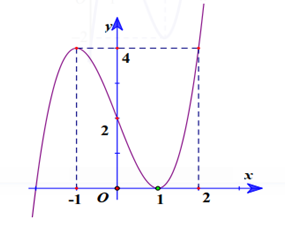
Đồ thị hàm số có bao nhiêu tiệm cận đứng.
Cho hàm số y = f(x) có đồ thị như hình bên:

Đồ thị hàm số có bao nhiêu tiệm cận đứng.
Câu 13:
Cho hàm số y = f(x) có bảng biến thiên như sau
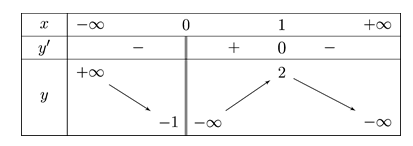
Mệnh đề nào dưới đây đúng?
Câu 14:
Bà Hoa gửi vào ngân hàng 120 triệu đồng theo hình thức lãi suất kép. Lãi suất ngân hàng là 8% năm và không thay đổi qua các năm bà gửi tiền. Sau ít nhất bao nhiêu năm thì bà Hoa có số tiền cả gốc lẫn lãi lớn hơn 180 triệu đồng?
Bà Hoa gửi vào ngân hàng 120 triệu đồng theo hình thức lãi suất kép. Lãi suất ngân hàng là 8% năm và không thay đổi qua các năm bà gửi tiền. Sau ít nhất bao nhiêu năm thì bà Hoa có số tiền cả gốc lẫn lãi lớn hơn 180 triệu đồng?
Câu 15:
Nguyên hàm F(x) của hàm số f(x) = x + sinx thỏa mãn F(0) = 19 là:
Nguyên hàm F(x) của hàm số f(x) = x + sinx thỏa mãn F(0) = 19 là:



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)