Câu hỏi:
12/11/2024 665Số hình đa diện lồi trong các hình dưới đây là:
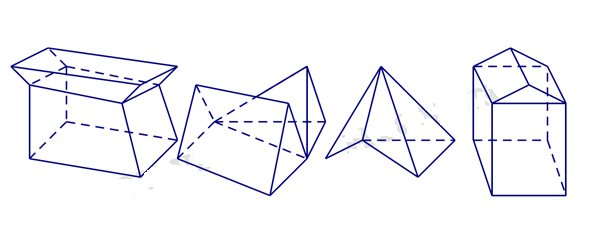
A. 3
B. 0
C. 1
D. 2
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
Lời giải
Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện giới hạn (H) được gọi là đa diện lồi.
Hoặc một khối đa diện là đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.
Do đó chỉ có 1 khối đa diện lồi.
*Phương pháp giải:
Sử dụng khái niệm hình đa diện lồi
*Lý thuyết:
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
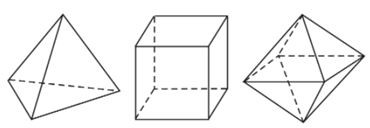
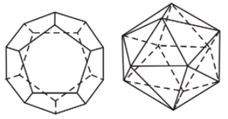
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
Xem thêm
Lý thuyết Khối đa diện lồi và khối đa diện đều (mới 2024 + Bài Tập) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho tứ diện OMNP có Om, ON, OP đôi một vuông góc. Tính thể tích V của khối tứ diện OMNP.
Câu 3:
Đường cong ở hình vẽ là đồ thị của một trong các hàm số dưới đây.
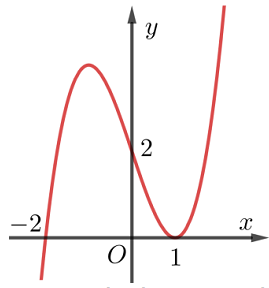
Hàm số đó là hàm số nào?
Câu 4:
Cho các số thực dương x, y thoả mãn 2x+y=54.Tìm giá trị nhỏ nhất Pmin của biểu thức P=2x+14y .
Câu 5:
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=mx−8x+2 có tiệm cận đứng
Câu 6:
Cho hàm số y=f(x)=a x3+bx2+cx+d với a≠0.Biết đồ thị hàm số có hai điểm cực trị là A(1;−1),B(−1;3). Tính f(4).
Câu 7:
Một kim tự tháp Ai Cập có hình dạng là một khối chóp tứ giác đều có độ dài cạnh bên là một số thực dương không đổi. Gọi α là góc giữa cạnh bên của kim tự tháp với mặt đáy. Khi thể tích của kim tự tháp lớn nhất, tính sinα.
Câu 8:
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a, các mặt bên tạo với đáy một góc 60∘. Tính diện tích S của mặt cầu ngoại tiếp hình chóp.
Câu 9:
Cho tứ diện đều ABCD có cạnh 2a. Tính bán kính r của mặt cầu tiếp xúc với tất cả các mặt của tứ diện
Câu 10:
Cho tam giác ABC. Tâp hợp các điểm M trong không gian thỏa mãn |→MA+→MB+→MC|=a (với a là số thực dương không đổi) là
Câu 11:
Cho Parabol (P):y=x2+2x−1, qua điểm M thuộc (P) kẻ tiếp tuyến với (P) cắt hai trục Ox, Oy lần lượt tại hai điểm A, B. Có bao nhiêu điểm M để tam giác ABO có diện tích bằng 14.
Câu 13:
Cho p, q là các số thực thỏa mãn:
m=(1e)2p−q,n=ep−2q, biết m > n.
So sánh p và q.



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)