Câu hỏi:
11/11/2024 1,635Số giao điểm tối đa của 10 đường thẳng phân biệt là
A. 50.
B. 120.
C. 100.
D. 45.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Lời giải:
Số giao điểm của 10 đường thẳng phân biệt tối đa đạt được khi bất kì hai đường thẳng nào cũng cắt nhau và các giao điểm là phân biệt.
⇒ số giao điểm bằng số cặp đường thẳng
⇒ số giao điểm tối đa là: (giao điểm).
*Phương pháp giải:
- Do là giao điểm thì sẽ là 2 đường thẳng cắt nhau nên ở đây sẽ dùng tổ hợp:
*Lý thuyến cần nắm về tổ hợp - xác suất
1. Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m+n cách thực hiện.
2. Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.
3. Hoán vị:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử.
- Số các hoán vị của n phần tử là: Pn = n(n-1)...2.1 = n!
4. Chỉnh hợp:
Cho tập hợp A gồm n phần tử (n ≥ 1).
- Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.
- Số các chỉnh hợp chập k của n phần tử là:
5. Tổ hợp:
Giả sử A có n phần tử (n ≥ 1).
- Mỗi tập hợp gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho. (1 ≤ k ≤ n).
Số các tổ hợp chập k của n phần tử là:
6. Công thức nhị thức Niu-tơn:
(a + b)n = Cn0an + Cn1an - 1b + … + Cnkan - kbk + … + Cnn-1abn-1 + Cnnbn
7. Phép toán trên các biến cố:
- Giả sử A là biến cố liên quan đến một phép thử.
Khi đó, tập Ω\A được gọi là biến cố đối của biến cố A, kí hiệu là A−.
- Giả sử A và B là hai biến cố liên quan đến một phép thử:
+ Tập A ⋃ B được gọi là hợp của các biến cố A và B.
+ Tập A ⋂ B được gọi là giao của các biến cố A và B.
+ Nếu A ⋂ B = ∅ thì ta nói A và B xung khắc.
8. Xác suất của biến cố:
Giả sử A là biến cố liên quan đến phép thử chỉ có một số hữu hạn kết quả đồng khả năng xuất hiện. Khi đó, xác suất của biến cố A là:
trong đó: n(A) là số phần tử của A; còn n(Ω) là số các kết quả có thể xảy ra của phép thử.
9. Tính chất của xác suất:
Giả sử A và B là các biến cố liên quan đến một phép thử có một số hữu hạn kết quả đồng khả năng xuất hiện.
P(∅) = 0, P(Ω) = 1
0 ≤ P(A) ≤ 1, với mọi biến cố A.
Nếu A và B xung khắc, thì P(AB) = P(A) + P(B) (công thức cộng xác suất)
Với mọi biến cố A, ta có: P(A−) = 1 – P(A).
A và B là hai biến cố độc lập khi và chỉ khi P(A.B) = P(A).P(B).
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Tổ hợp - xác suất hay, chi tiết
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Ba cạnh của một tam giác vuông có độ dài là các số nguyên dương lập thành một cấp số cộng. Thế thì một cạnh có thể có độ dài bằng bao nhiêu?
Câu 2:
Cho tập . Có bao nhiêu tập X con của A thỏa mãn chứa số 1 mà không chứa số 2?
Câu 3:
Cho hàm số có đồ thị (C). Có bao nhiêu điểm sao cho tổng khoảng cách từ M đến hai đường tiệm cận bằng 2?
Câu 4:
Hằng ngày mực nước biển của con kênh lên, xuống theo thủy triều. Độ sâu h(m) của mực nước trong kênh được tính tại thời điểm t (giờ), trong một ngày được tính bởi công thức . Hỏi trong một ngày có mấy thời điểm mực nước của con kênh đạt độ sâu lớn nhất?
Câu 7:
Cho phương trình Gọi là hai nghiệm của phương trình. Khi đó giá trị biểu thức là
Câu 8:
Cho hình chóp S.ABC có AB, AC, SA đôi một vuông góc với nhau, Tính thể tích của khối chóp S.ABC.
Câu 9:
Đường cong trong hình bên là của đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
Câu 10:
Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là
Câu 13:
Cho tam giác ABC có . Phép tịnh tiến biến tam giác ABC thành tam giác A′B′C′. Tọa độ trọng tâm tam giác A′B′C′ là
Câu 15:
Cho . Biết ảnh của (P) qua phép tịnh tiến theo vecto là (P’): . Tính giá trị biểu thức .

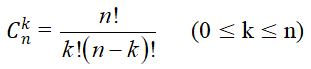
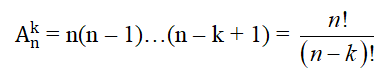
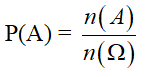


![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)