Người ta xây một sân khấu với mặt sân có dạng hợp của hai hình tròn giao nhau. Bán kính của hai hình tròn là 20 mét và 15 mét. Khoảng cách giữa hai tâm của hai hình tròn là 30 mét. Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 ngàn đồng và chi phí làm mỗi mét vuông phần còn lại là 100 ngàn đồng. Hỏi số tiền làm mặt sân của sân khấu gần với số nào trong các số dưới đây?

Cho hàm số $f\left(x\right)$  có bảng xét dấu của đạo hàm như sau:

Hàm số $y=3f\left(x+2\right)-x^3+3\text{x}$  đồng biến trên khoảng nào dưới đây?

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh $AB=a$ , $BC=2\text{a}$ . Hai mặt bên $\left(SAB\right)$  và $\left(SA\text{D}\right)$  cùng vuông góc với mặt phẳng đáy $\left(ABC\text{D}\right)$ , cạnh $SA=a\sqrt{15}$ . Tính theo a thể tích V của khối chóp S.ABCD.

Cho hàm số $y=f\left(x\right)$ . Hàm số $y=f^{\text{'}}\left(x\right)$  có đồ thị như sau:

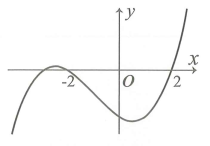
Bất phương trình $f\left(x\right)>x^2-2\text{x}+m$  nghiệm đúng với mọi $x\in \left(1;2\right)$  khi và chỉ khi

Bất phương trình $3^{2\text{x}+1}-{7.3}^x+2>0$  có nghiệm

Cho x, y là các số thực dương tùy ý, đặt ${\log }_{3}x=a,{\text{ log}}_{3}y=b$ . Chọn mệnh đề đúng.

Trong không gian với hệ tọa độ Oxyz, viết phương trình đường vuông góc chung của hai đường thẳng $d:\frac{x-2}{2}=\frac{y-3}{3}=\frac{z+4}{-5}$  và $d^{\text{'}}:\frac{x+1}{3}=\frac{y-4}{-2}=\frac{z-4}{-1}$ .

Tích tất cả các số thực m để hàm số $y=\left|\frac{4}{3}{x}^3-6{\text{x}}^2+8\text{x}+m\right|$  có giá trị nhỏ nhất trên đoạn $\left[0;3\right]$  bằng 18 là

Cho hàm số $y=f\left(x\right)$  có đồ thị như hình bên dưới.

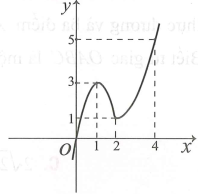
Có bao nhiêu giá trị nguyên của tham số m để phương trình $f\left(\frac{6{\text{x}}^2}{x^4+x^2+1}+2\right)+1=m$  có nghiệm?

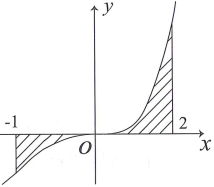
Gọi S là diện tích hình phẳng $\left(H\right)$  giới hạn bởi các đường $y=f\left(x\right)$ , trục hoành và 2 đường thẳng $x=-\mathrm{1,}x=2$  trong hình vẽ bên.

Đặt: $S_1=\underset{1}{\overset{0}{\int }}f\left(x\right)d\text{x};{\text{ S}}_2=\underset{0}{\overset{2}{\int }}f\left(x\right)d\text{x}$ . Mệnh đề nào sau đây đúng

Cho phương trình ${\log }_2{\left(2x-1\right)}^2=2{\log }_2\left(x-2\right)$  Số nghiệm thực của phương trình là:

Cho mặt cầu $S_{\left(O;r\right)}$  có diện tích đường tròn lớn là 2π. Khi đó, mặt cầu $S_{\left(O;r\right)}$  có bán kính là:

Kí hiệu $z_1,{\text{ z}}_2$  là hai nghiệm phức của phương trình $z^2-3\text{x}+5=0$ . Giá trị của $\left|z_1\right|+\left|z_2\right|$  bằng

Cho hàm số $f\left(x\right)$  có đạo hàm xác định trên $ℝ$  và thỏa mãn $f^{\text{'}}\left(x\right)+4\text{x}-6\text{x}.e^{x^2-f\left(x\right)-2019}=0$  và $f\left(0\right)=-2019$ . Số nghiệm nguyên dương của bất phương trình $f\left(x\right)<7$  là

Biết rằng phương trình ${\log }_3\left(3^{x+1}-1\right)=2\text{x}+{\log }_{\frac{1}{3}}2$  có hai nghiệm $x_1$  và $x_2$ . Hãy tính tổng $S={27}^{x_1}+{27}^{x_2}$ .

Cho x, y là các số dương thỏa mãn ${\log }_2\frac{x^2+5y^2}{x^2+10\text{x}y+y^2}+1+x^2-10\text{x}y+9y^2\le 0$ . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $P=\frac{x^2+xy+9y^2}{xy+y^2}$ . Tính $T=10M-m$ .