Câu hỏi:
21/07/2024 853Cho hàm số có đồ thị như hình bên dưới.
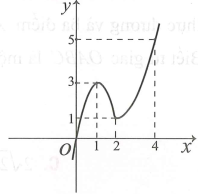
Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm?
A. 4
B. 2
C. 5
D. 3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Cách 1: Phương pháp tự luận truyền thống
Đặt .
Ta có .
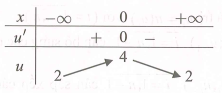
Bài toán trở thành tìm m nguyên để phương trình có nghiệm .
Dựa vào đồ thị đề bài cho suy ra có nghiệm .
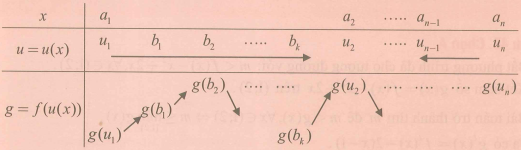
Cách 2: Phương pháp ghép trục
có cực trị hoành độ .
Đặt .
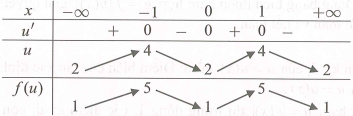
Suy ra có nghiệm .
|
Các bước thực hiện phương pháp ghép trục: Bước 1:Tìm tập xác định của hàm , giả sử ta được tập xác định . Ở đây có thể là . Bước 2: Xét sự biến thiên của và hàm (Có thể làm gộp trong bước 3 nếu đơn giản). Bước 3: Lập bảng biến thiên tổng hợp xét sự tương quan giữa và . Bảng này thường có 3 hàng dạng
Cụ thể các thành phần trong bảng biến thiên như sau Hàng 1: Xác định các điểm kỳ dị của hàm , sắp xếp các điểm này theo thứ tự tăng dần từ trái qua phải, giả sử: (xem chú ý 1). Hàng 2: Điền các giá trị với . Trên mỗi khoảng cần bổ sung các điểm kỳ dị của hàm . Trên mỗi khoảng cần sắp xếp các điểm theo thứ tự chẳng hạn: hoặc (xem chú ý 2). Hàng 3: Xét chiều biến thiên của hàm dựa vào bảng biến thiên của hàm bằng cách hoán đổi: u đóng vai trò của x; đóng vai trò của . Sau khi hoàn thiện bảng biến thiên hàm hợp ta thấy được hình dạng đồ thị hàm này. Bước 4: Dùng bảng biến thiên hàm hợp giải quyết các yêu cầu đặt ra trong bài toán và kết luận. Chú ý 1: + Các điểm kỳ dị của gồm: Điểm biên của tập xác định D và các điểm cực trị của . + Nếu xét hàm thì trong dòng 1, các điểm kỳ dị còn có nghiệm của phương trình (là hoành độ giao điểm của với trục Ox). + Nếu xét hàm thì trong dòng 1, các điểm kỳ dị còn có số 0 (là hoành độ giao điểm của với trục Oy). Chú ý 2: + Có thể dùng thêm các mũi tên để thể hiện chiều biến thiên của . + Điểm kỳ dị của gồm: Các điểm tại đó và không xác định; các điểm cực trị hàm số . + Nếu xét hàm thì trong dòng 2, các điểm kỳ dị còn có nghiệm của phương trình (là hoành độ giao điểm của với trục Ox). + Nếu xét hàm thì trong dòng 2, các điểm kỳ dị còn có số 0 (là hoành độ giao điểm của với trục Oy). |
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số có bảng xét dấu của đạo hàm như sau:

Hàm số đồng biến trên khoảng nào dưới đây?
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh , . Hai mặt bên và cùng vuông góc với mặt phẳng đáy , cạnh . Tính theo a thể tích V của khối chóp S.ABCD.
Câu 3:
Cho hàm số . Hàm số có đồ thị như sau:
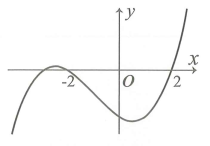
Bất phương trình nghiệm đúng với mọi khi và chỉ khi
Câu 6:
Trong không gian với hệ tọa độ Oxyz, viết phương trình đường vuông góc chung của hai đường thẳng và .
Câu 7:
Tích tất cả các số thực m để hàm số có giá trị nhỏ nhất trên đoạn bằng 18 là
Câu 8:
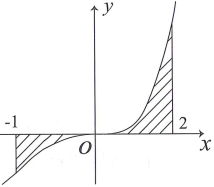
Gọi S là diện tích hình phẳng giới hạn bởi các đường , trục hoành và 2 đường thẳng trong hình vẽ bên.
Đặt: . Mệnh đề nào sau đây đúng
Câu 10:
Cho mặt cầu có diện tích đường tròn lớn là 2π. Khi đó, mặt cầu có bán kính là:
Câu 12:
Cho hàm số có đạo hàm xác định trên và thỏa mãn và . Số nghiệm nguyên dương của bất phương trình là
Câu 14:
Cho x, y là các số dương thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của . Tính .
Câu 15:
Cho hàm số có đạo hàm . Hàm số đã cho đồng biến trên khoảng nào dưới đây?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)