Một ô tô đang chạy với vận tốc 10m/s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chạm dần đều với vận tốc $v\left(t\right)=-2t+10\left(m/s\right)$ , trong đó  t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quãng đường ô tô di chuyển được trong 8 giây cuối cùng. 

Đáp án đúng:  A.

* Lời giải:

Khi xe dừng hẳn thì vận tốc bằng 0.

Nên thời gian kể từ lúc đạp phanh đến lúc ô tô dừng hẳn là -2t +10 = 0Û t = 5s

Quãng đường ô tô đi được từ lúc đạp phanh đến lúc ô tô dừng hẳn là

Như vậy trong 8 giây cuối thì có 3 giây ô tô đi với vận tốc  10m/s và  5s ô tô chuyển động chậm dần đều.

Quãng đường ô tô đi được trong 3 giây trước khi đạp phanh là

 Vậy trong 8 giây cuối ô tô đi được quang đường$S_1=3.10=30m$

* Phương pháp giải:

Ta sử dụng quãng đường đi được trong khoảng thời gian từ $t_1\to t_2$là

 $S={\int }_{t_1}^{t_2}v\left(t\right)dt$

Với v (t) là hàm vận tốc.

Chú ý rằng khi xe dừng hẳn thì vận tốc bằng 0.

* Lý thuyết nắm thêm

- Chuyển động thẳng biến đổi đều là chuyển động có quỹ đạo là đường thẳng có độ lớn của vận tốc tức thời hoặc tăng đều hoặc giảm đều theo thời gian.

- Chuyển động thẳng có độ lớn của vận tốc tức thời giảm đều theo thời gian gọi là chuyển động thẳng chậm dần đều.

- Giả sử có một chất điểm M, xuất phát từ một điểm A có tọa độ x₀ trên đường thẳng Ox, chuyển động thẳng nhanh dần đều với vận tốc đầu v₀ và với gia tốc a.

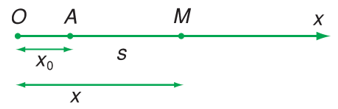
- Chọn chiều dương là chiều chuyển động của vật.

- Vật chuyển động chậm dần đều nên a.v₀ < 0 => a và v₀ trái dấu.

Phương trình chuyển động của chất điểm chuyển động chậm dần đều:

$x=x_0+v_{0}t+\frac{1}{2}a{t}^2$

Trong đó:

+ x_o: tọa độ ban đầu của vật tại thời điểm t₀ (m)

+ x: tọa độ của vật sau thời gian chuyển động t (m)

+ v₀: vận tốc chuyển động của vật (m/s)

+ a: gia tốc chuyển động của vật (m/s²)

- Quãng đường đi được của chuyển động thẳng chậm dần đều:

$s=v_{0}t-\frac{1}{2}a{t}^2$

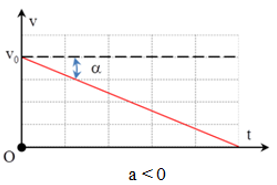
- Nếu chọn chiều của các vận tốc là chiều dương thì v < v₀ và Δv < 0. Gia tốc a có giá trị âm, tức là ngược dấu với vận tốc:

$a=\frac{∆v}{∆t}=\frac{v-v_0}{t-t_0}$

- Nếu lấy gốc thời gian ở thời điểm t₀ = 0 thì công thức tính vận tốc:

v = v₀ - a.t

- Công thức liên hệ giữa gia tốc, vận tốc và quãng đường đi được của chuyển động thẳng biến đổi đều:

v² - v₀² = 2.(-a).s

Chú ý: Trong chuyển động chậm dần đều có lúc vật sẽ dừng lại (v = 0). Nếu gia tốc của vật vẫn được duy trì thì vật sẽ chuyển động nhanh dần đều về phía ngược lại.

- Đồ thị tọa độ theo thời gian (x – t): hình dạng là một nhánh parabol

+ Đồ thị vật chuyển động chậm dần đều

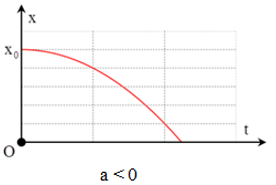
- Đồ thị vận tốc theo thời gian (v – t): hình dạng là đường thẳng xiên góc.

Hệ số góc của đường biểu diễn v – t bằng gia tốc của chuyển động:

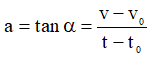
+ Đồ thị vật chuyển động chậm dần đều

Xem thêm các bài viết liên quan hay, chi tiết:

Phương trình chuyển động thẳng chậm dần đều và cách giải các dạng bài tập (2024) chi tiết nhất