Câu hỏi:
19/07/2024 164Kí hiệu z1, z2 là các nghiệm phức của phương trình 2z2-3z+7=0. Tìm các giá trị của S = z1+z2-z1z2.
A. S = 2.
B. S = -2.
C. S = 5.
D. S = -5.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn B.
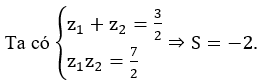
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trên tập hợp số phức, cho phương trình z2+bz+c=0 với b, c∈ℚ Biết rằng hai nghiệm của phương trình có dạng w + 3 và 2w – 6i +1 với w là một số phức. Tính S=b3-c2.
Câu 2:
Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số y=x3+3x2-9x+2m+1 và trục Ox có đúng hai điểm chung phân biệt. Tính tổng T của các phần tử thuộc tập S.
Câu 3:
Trong không gian Oxyz, cho mặt phẳng (P): 2x + 2y - z - 12 = 0 và hai điểm A(1;3;16), B(5;10;21). Gọi ∆ là đường thẳng đi qua điểm A đồng thời vuông góc với mặt phẳng (P). Khoảng cách từ điểm B đến đường thẳng bằng
Câu 4:
Trong không gian tọa độ với hệ tọa độ Oxyz, cho ba điểm A(1;2;-1), B(2;-1;3) và C(-3;5;1). Gọi điểm D(a;b;c) thỏa mãn tứ giác ABCD là hình bình hành. Tính tổng T = a + b + c.
Câu 5:
Cho tứ diện ABCD có BC = 3, CD = 4, . Góc giữa hai đường thẳng AB và CD bằng . Tính thể tích khối cầu ngoại tiếp tứ diện ABCD
Câu 6:
Hàm số y = f(x) xác định và có đạo hàm trên R\{-2;2} có bảng biến thiên như sau.
Hàm số y = f(x) xác định và có đạo hàm trên R\{-2;2} có bảng biến thiên như sau. 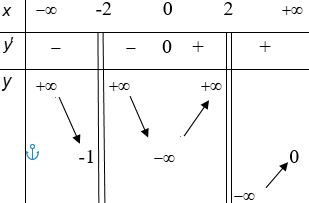
Gọi k, l lần lượt là số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số Tính giá trị k + l
Câu 7:
Cho hàm số với a, b là các số hữu tỉ thỏa mãn điều kiện Tính T = a + b.
Câu 9:
Trong mặt phẳng Oxy cho hai điểm A(2;1), B(-1;2). Xác định tọa độ điểm C thuộc Ox sao cho A, B, C thẳng hàng.
Câu 11:
Trong không gian Oxyz cho mặt phẳng (P): 2x + 2y - z + 4 = 0 và các điểm A(2;1;2); B(3;-2;2). Điểm M thuộc mặt phẳng (P) sao cho các đường thẳng MA; MB luôn tạo với mặt phẳng (P) các góc bằng nhau. Biết rằng điểm M thuộc đường tròn (C) cố định. Tìm tọa độ tâm của đường tròn (C).
Câu 12:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau và Phương trình mặt phẳng (P) chứa đường thẳng d1 và song song với đường thẳng d2 là
Câu 13:
Trong không gian với hệ tọa độ Oxyz cho đường thẳng và mặt phẳng (P): 2x - 2y + z + 2 = 0. Mặt phẳng (Q) chứa và tọa với (P) một góc nhỏ nhất có phương trình dạng ax + by + cz + 34 = 0. Tính
Câu 14:
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số f(x) = trên đoạn [-4;-1]. Tính T = M + m.
Câu 15:
Cho đồ thị hàm số y = f(x) có đạo hàm trên R thỏa mãn f(2) = f(-2) = 0 và đồ thị hàm số y = f'(x) có dạng như hình vẽ. Hàm số y = nghịch biến trên khoảng nào trong các khoảng sau?




![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)