Câu hỏi:
16/07/2024 355Khối lăng trụ đều ABCD.A’B’C’D’ có thể tích 24cm3. Tính thể tích V của khối tứ diện ACB’D’.
A. V=8cm3
B. V=6cm3
C. V=12cm3
D. V=4cm3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
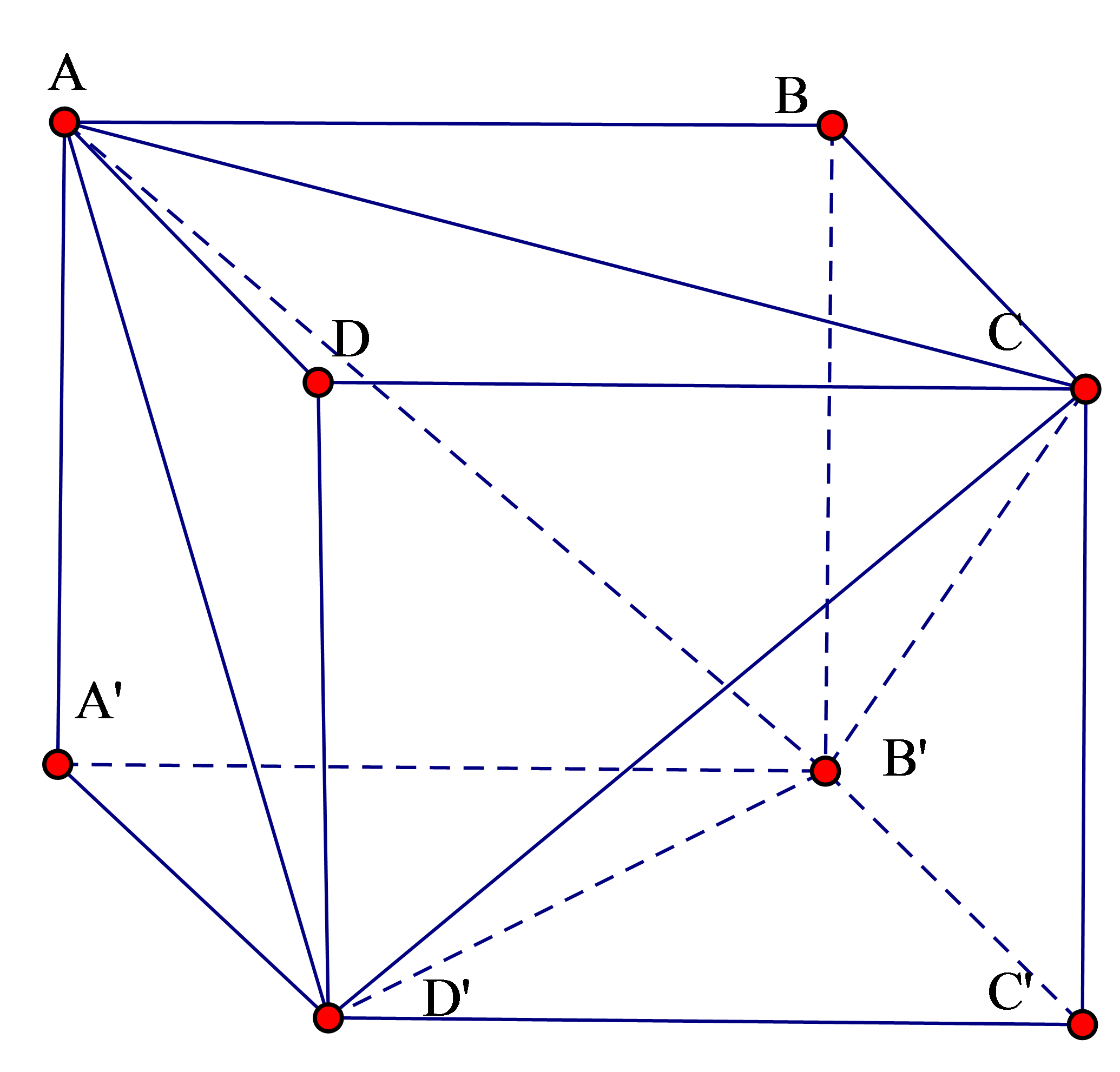
Gọi độ dài cạnh đáy là a, độ dài cạnh bên là b ta có:
VABCD.A'
Tứ diện ACB'D' có các cặp đối bằng nhau
Áp dung công thức tính thể tích của tứ diện có các cặp đối bằng nhau ta có:
(Do tính đối xứng ta có thể tính:
)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng (ABCD); góc giữa hai mặt phẳng (SBC) và (ABCD) bằng Khi đó khối chóp S.ABC có thể tích là
Câu 7:
Trong mặt phẳng với hệ tọa độ Oxy, cho parabol và parabol (P') là ảnh của (P) qua phép tịnh tiến theo , với 0<b<4. Gọi A,B là giao điểm của (P) với Ox, M,N là giao điểm của (P') với Ox , I, J lần lượt là đỉnh của (P) và (P'). Tìm tọa độ điểm J để diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN.
Câu 8:
Cho khối lăng trụ tam giác đều ABC.A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng . Tính thể tích của khối lăng trụ .
Câu 10:
Cho hàm số có đạo hàm là hàm số y=f'(x) có đồ thị như hình vẽ bên.
Biết rằng đồ thị hàm số y=f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng bao nhiêu?
Câu 12:
Trong một kì thi. Thí sinh được phép thi 3 lần. Xác suất lần đầu vượt qua kì thi là 0,9. Nếu trượt lần đầu thì xác suất vượt qua kì thi lần hai là 0,7. Nếu trượt cả hai lần thì xác suất vượt qua kì thi ở lần thứ ba là 0,3. Xác suất để thí sinh thi đậu là
Câu 13:
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy và SA=a.Tính thể tích khối chóp S.ABC.
Câu 14:
Diện tích một mặt của một hình lập phương là 9. Thể tích khối lập phương đó là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)