Câu hỏi:
13/11/2024 267
Hàm số nào dưới đây có bảng biến thiên như sau?
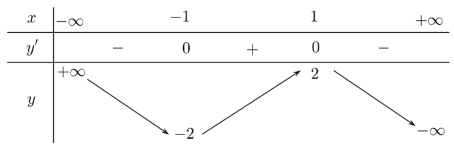
Hàm số nào dưới đây có bảng biến thiên như sau?

A. y = x3 – 3x.
A. y = x3 – 3x.
B. y = x2 – 2x.
B. y = x2 – 2x.
C. y = −x3 + 3x.
D. y = −x2 + 2x.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: C
*Lời giải:
Dựa vào bảng biến thiên trên, ta nhận thấy đây là hàm số bậc ba có dạng y = ax3 + bx2 + cx + d với a ≠ 0.
Mà Þ a < 0.
Do đó trong các hàm số đã cho, có duy nhất hàm số y = −x3 + 3x thoả mãn.
*Phương pháp giải:
- Nhìn vào bảng biến thiên, ta nhận định hàm số thuộc hàm số bậc 3: y = ax3 + bx2 + cx + d (a ≠ 0).
- Dựa vào dạng của đồ thị và bảng biến thiên: Ta thấy giá trị a < 0
*Lý thuyến cần nắm và các dạng toán về khảo sát sự biến thiên đồ thị hàm số:
1. Tập xác định
Tìm tập xác định của hàm số.
2. Sự biến thiên.
+ Xét chiều biến thiên của hàm số.
- Tính đạo hàm y’.
- Tìm các điểm tại đó đạo hàm y’ bằng 0 hoặc không xác định.
- Xét dấu đạo hàm y’ và suy ra chiều biến thiên của hàm số.
+ Tìm cực trị
+ Tìm các giới hạn tại vô cực, các giới hạn vô cực và tìm các tiệm cận (nếu có).
+ Lập bảng biến thiên (ghi các kết quả tìm được vào bảng biến thiên).
3. Đồ thị
Dựa vào bảng biến thiên và các yếu tố ở trên để vẽ đồ thị hàm số.
- Chú ý:
1. Nếu hàm số tuần hoàn với chu kì T thì chỉ cần khảo sát sự biến thiên và vẽ đồ thị trên một chu kì, sau đó tịnh tiến đồ thị song song với trục Ox.
2. Nên tính thêm tọa độ một số điểm, đặc biệt là tọa độ các giao điểm của đồ thị với các trục tọa độ.
3. Nên lưu ý tính chẵn, lẻ của hàm số và tính đối xứng của đồ thị để vẽ cho chính xác.
Dạng của đồ thị hàm số bậc ba y = ax3 + bx2 + cx + d (a ≠ 0).
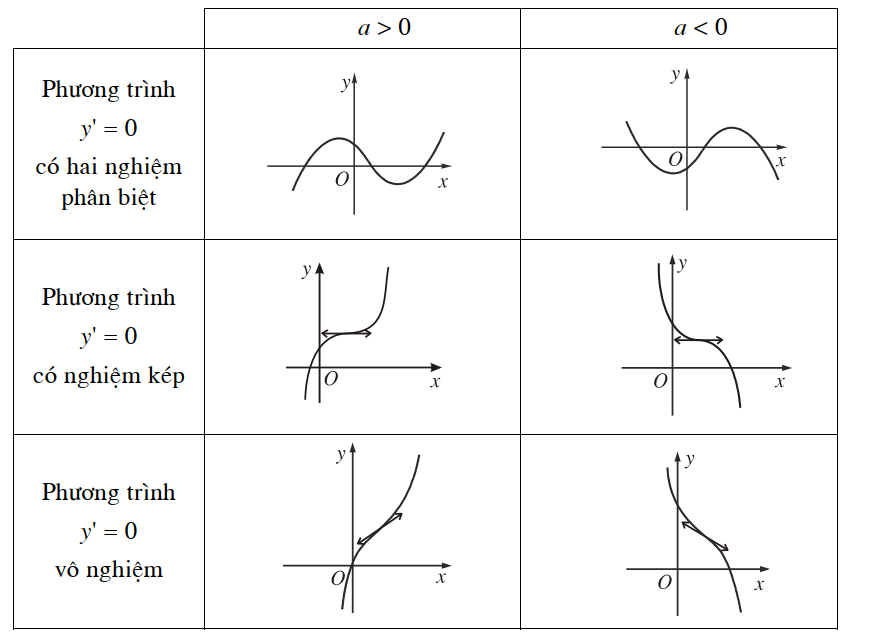
Dạng của đồ thị y = ax4 + bx2 + c (với a ≠ 0)
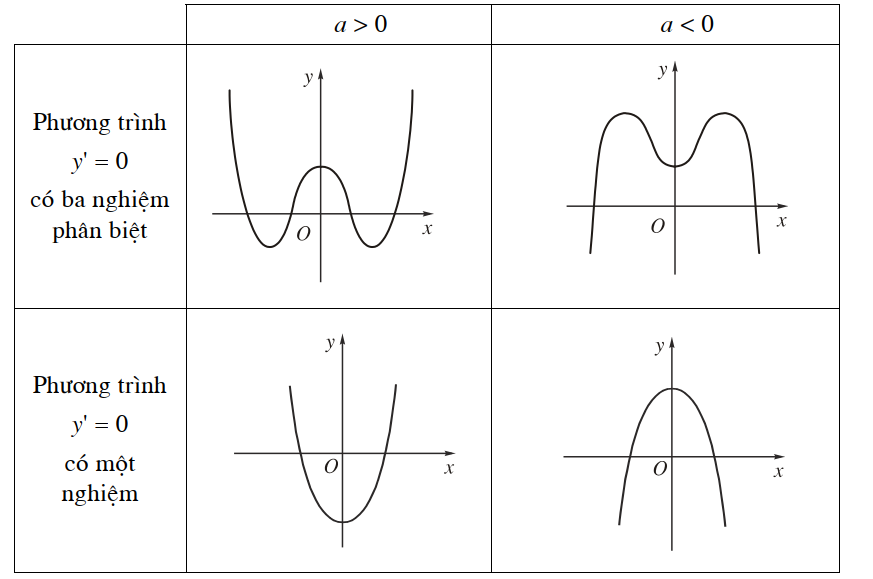
Dạng của đồ thị hàm số
Sự tương giao của các đồ thị.
Giả sử hàm số y = f(x) có đồ thị là (C1) và hàm số y = g(x) có đồ thị là (C2). Để tìm hoành độ giao điểm của (C1)và (C2), ta phải giải phương trình f(x) = g(x).
Giả sử phương trình trên có các nghiệm x0; x1; … khi đó, các giao điểm của (C1)và (C2) là M0 (x0; f(x0)); M1 (x1; f(x1))…..
Xem thêm các bài viết liên quan hay, chi tiết
Lý thuyết Khảo sát sự biến thiên và vẽ đồ thị của hàm số – Toán lớp 12 Cánh diều
Chuyên đề Khảo sát sự biến thiên và vẽ đồ thị hàm số (2024) - Toán 12
50 bài tập về sự đồng biến và nghịch biến của hàm số (có đáp án 2024) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x) = (a + 3)x4 – 2ax2 + 1 với a là tham số thực. Nếu = f(2) thì bằng
Cho hàm số f(x) = (a + 3)x4 – 2ax2 + 1 với a là tham số thực. Nếu = f(2) thì bằng
Câu 2:
Cho các số phức z1, z2, z3 thoả mãn 2|z1| = 2|z2| = |z3| = 2 và (z1 + z2)z3 = 2z1z2. Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng toạ độ. Diện tích tam giác ABC bằng
Cho các số phức z1, z2, z3 thoả mãn 2|z1| = 2|z2| = |z3| = 2 và (z1 + z2)z3 = 2z1z2. Gọi A, B, C lần lượt là các điểm biểu diễn của z1, z2, z3 trên mặt phẳng toạ độ. Diện tích tam giác ABC bằng
Câu 3:
Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x – 2y + 2z + 3 = 0 là
Trong không gian Oxyz, cho điểm A(1; 2; 3). Phương trình của mặt cầu tâm A và tiếp xúc với mặt phẳng x – 2y + 2z + 3 = 0 là
Câu 4:
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 3 (tham khảo hình bên dưới).
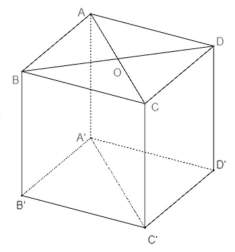
Khoảng cách từ B đến mặt phẳng (ACC’A’) bằng
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 3 (tham khảo hình bên dưới).

Khoảng cách từ B đến mặt phẳng (ACC’A’) bằng
Câu 5:
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 2. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 2. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng
Câu 6:
Gọi z1, z2 là hai nghiệm phức của phương trình z2 – 2z + 5 = 0. Khi đó z12 + z22 bằng
Gọi z1, z2 là hai nghiệm phức của phương trình z2 – 2z + 5 = 0. Khi đó z12 + z22 bằng
Câu 7:
Biết F(x) và G(x) là hai nguyên hàm của hàm số f(x) trên ℝ và = F(2) – G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x), y = G(x), x = 0 và x = 2. Khi S = 6 thì a bằng
Biết F(x) và G(x) là hai nguyên hàm của hàm số f(x) trên ℝ và = F(2) – G(0) + a (a > 0). Gọi S là diện tích hình phẳng giới hạn bởi các đường y = F(x), y = G(x), x = 0 và x = 2. Khi S = 6 thì a bằng
Câu 9:
Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w = 1 – 4i?
Số phức nào dưới đây có phần ảo bằng phần ảo của số phức w = 1 – 4i?
Câu 10:
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, cạnh bên AA’ = 2a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60°. Thể tích của khối lăng trụ đã cho bằng
Cho khối lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, cạnh bên AA’ = 2a, góc giữa hai mặt phẳng (A’BC) và (ABC) bằng 60°. Thể tích của khối lăng trụ đã cho bằng
Câu 11:
Xét tất cả các số thực x, y sao cho ≥ với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 – 6x – 8y bằng
Xét tất cả các số thực x, y sao cho ≥ với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 – 6x – 8y bằng
Câu 12:
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên như sau
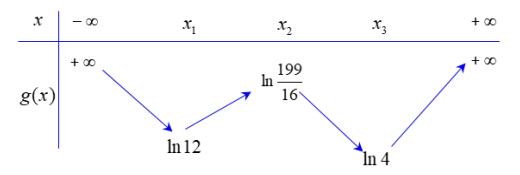
Diện tích hình phẳng giới hạn bởi các đường y = f'(x) và y = g'(x) thuộc khoảng nào dưới đây?
Cho hàm số bậc bốn y = f(x). Biết rằng hàm số g(x) = ln f(x) có bảng biến thiên như sau

Diện tích hình phẳng giới hạn bởi các đường y = f'(x) và y = g'(x) thuộc khoảng nào dưới đây?
Câu 13:
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Câu 15:
Trong không gian Oxyz, cho điểm M(2; −2; 1) và mặt phẳng (P): 2x – 3y – z + 1 = 0. Đường thẳng đi qua M và vuông góc với mặt phẳng (P) có phương trình là
Trong không gian Oxyz, cho điểm M(2; −2; 1) và mặt phẳng (P): 2x – 3y – z + 1 = 0. Đường thẳng đi qua M và vuông góc với mặt phẳng (P) có phương trình là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)