Câu hỏi:
18/11/2024 120
Có bao nhiêu khối đa diện đều
Có bao nhiêu khối đa diện đều
A. 3
B. 4
C. 6
D. 5
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
*Lời giải:
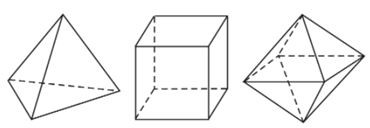
Có 5 khối đa diện đều: tứ diện đều; hình lập phương; bát diện đều; 12 mặt đều; 20 mặt đều.
*Phương pháp giải:
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
*Lý thuyết cần nắm và dạng bài toán về khối đa diện đều:
Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
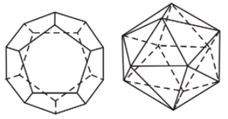
Bảng tóm tắt của năm loại khối đa diện đều.

Thể tích của khối đa diện
Người ta chứng minh được rằng: có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thỏa mãn các tính chất sau:
a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.
b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2).
c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:
V(H) = V(H1) + V(H2).
Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).
Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.
- Định lí : Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.
Thể tích của khối lăng trụ.
Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
Thể tích khối chóp.
Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là: .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Khối đa diện lồi và khối đa diện đều (mới 2024 + Bài Tập) – Toán 12
Toán 12 Bài 2 giải vở bài tập: Khối đa diện lồi và khối đa diện đều
50 bài toán về nhận biết khối đa diện lồi, đều (có đáp án 2024) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ:
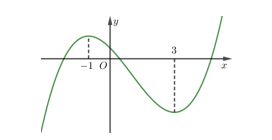
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số có 3 điểm cực trị. Tổng các phần tử của S là:
Cho hàm số bậc ba y = f(x) có đồ thị như hình vẽ:

Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số có 3 điểm cực trị. Tổng các phần tử của S là:
Câu 2:
Đường cong ở hình bên dưới là đồ thị của hàm số với a, b, c, d là các số thực. Giá trị nhỏ nhất của hàm số trên đoạn [-1; 0] là
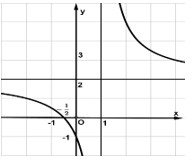
Câu 3:
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Thể tích khối tứ diện ABDB' bằng
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Thể tích khối tứ diện ABDB' bằng
Câu 5:
Cho hình lăng trụ ABCD.A'B'C'D' đáy là hình bình hành. Thể tích khối tứ diện BCDA' là
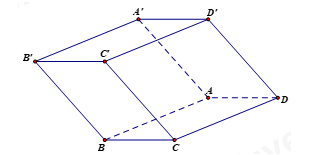
Câu 8:
Trong không gian Oxyz đường thẳng Ox có phương trình nào dưới đây
Trong không gian Oxyz đường thẳng Ox có phương trình nào dưới đây
Câu 9:
Trong không gian Oxyz, gọi A là điểm thuộc mặt cầu tâm I bán kính R. Chọn phương án đúng.
Trong không gian Oxyz, gọi A là điểm thuộc mặt cầu tâm I bán kính R. Chọn phương án đúng.
Câu 10:
Trong không gian Oxyz tọa độ điểm đối xứng của điểm M(0; 1; 2) qua mặt phẳng x + y + z = 0
Trong không gian Oxyz tọa độ điểm đối xứng của điểm M(0; 1; 2) qua mặt phẳng x + y + z = 0
Câu 11:
Cho hình lăng trụ . Số đoạn thẳng có hai đỉnh là đỉnh hình lăng trụ là
Cho hình lăng trụ . Số đoạn thẳng có hai đỉnh là đỉnh hình lăng trụ là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)