Cho tam giác ABC có đường cao AI. Từ A kẻ tia Ax vuông góc AC, từ B kẻ tia By song song AC. Gọi M là giao điểm của tia Ax và tia By. Nối M với trung điểm P của AB, đường thẳng MP cắt AC tại Q và đường thẳng BQ cắt AI tại H.

a) Tứ giác AMBQ là hình gì?

b) Chứng minh CH vuông góc AB.

c) Chứng minh tam giác PIQ cân.

*Lời giải:

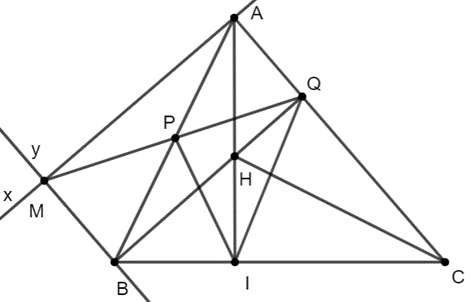
Vì Ax ⊥ AC ⇒ AM ⊥ AC

mà BM // AC

⇒ AM ⊥ BM

Chứng minh tương tự ⇒ AQ // BM và BM // AQ (cmt)

Suy ra AMBQ là hình bình hành.

Mà $\widehat{AMB}=\widehat{MBQ}=\widehat{ABQ}=\widehat{MAQ}={90}^o$.

Vậy AMBQ là hình chữ nhật.

b) BQ ⊥ AC (cmt) mà $BQ\cap AI=H$

Suy ra H là trực tâm của tam giác ABC.

Do đó: CH ⊥ AB

c) AMBQ là hình chữ nhật mà $AB\cap QM=P$

⇒ P là trung điểm AB và P là trung điểm QM

$\mathrm{\Delta }ABI$ vuông tại I có đường trung tuyến IP

⇒ $IP=\frac{1}{2}AB$

⇒ IP = PQ

⇒ $\mathrm{\Delta }IPQ$ cân tại P.

*Phương pháp giải:

Năm vững dấu hiệu nhận biết các hình để chứng minh

Nắm lại lý thuyết và cách chứng minh các đường trung trực, trung tuyến,...

*Lý thuyết nắm thêm

1. Định nghĩa

Hình bình hành là tứ giác có các cặp cạnh đối song song

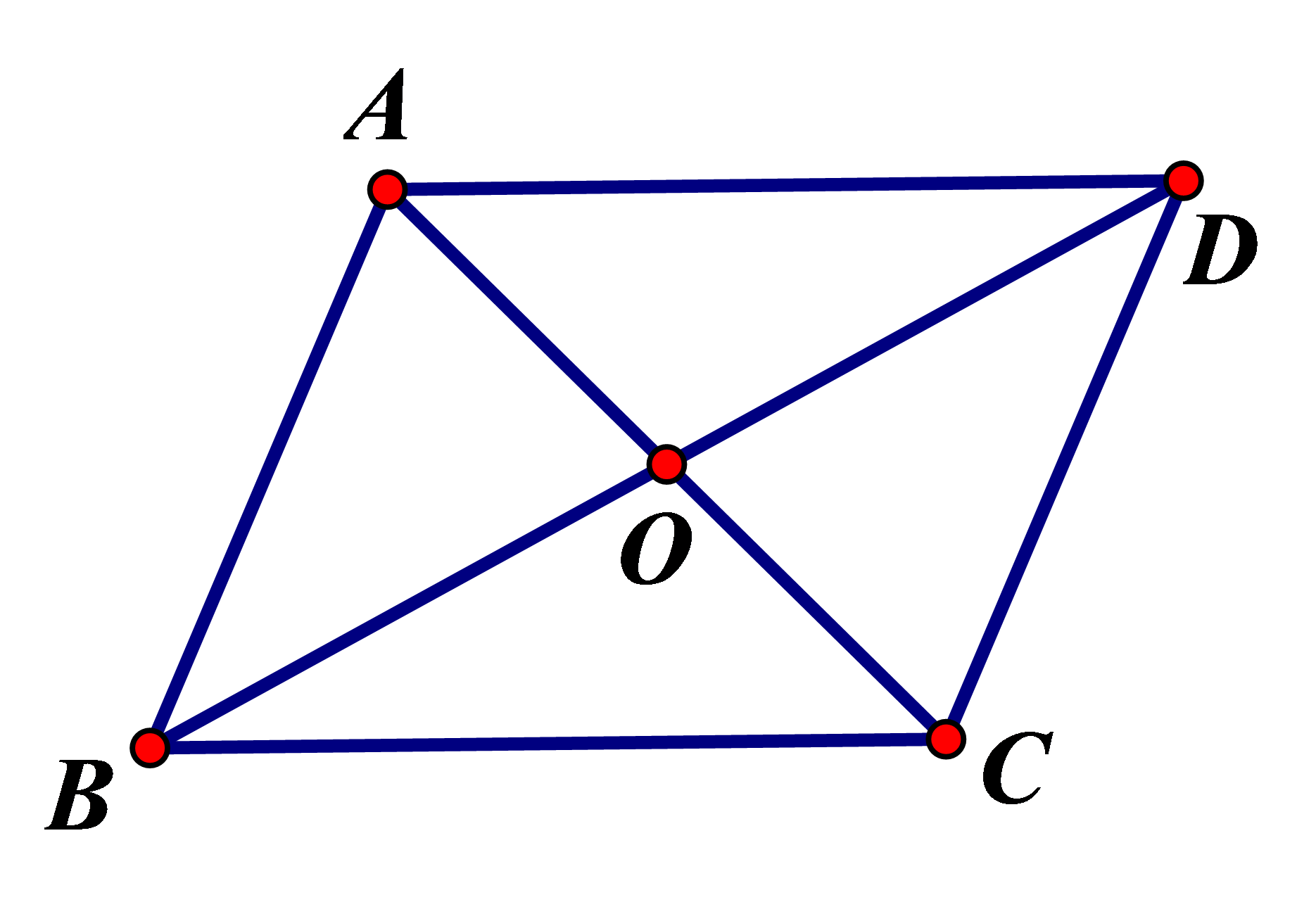
Tứ giác ABCD là hình bình hành$\iff \left\{\begin{array}{l}AB//CD\\ AD//BC\end{array}\right.$

2. Tính chất: Trong hình bình hành

a) Các cạnh đối bằng nhau;

b) Các góc đối bằng nhau;

c) Hai đường chéo cắt nhau tại trung điểm mỗi đường.

3. Dấu hiệu nhận biết

a) Tứ giác có các cạnh đối song song là hình bình hành;

b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;

c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;

d) Tứ giác có các góc đối bằng nhau là hình bình hành;

e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

II. Các dạng toán và phương pháp giải

Dạng 1. Vận dụng tính chất của hình bình hành để chứng minh các tính chất hình học

Phương pháp giải: Vận dụng định nghĩa, các tính chất về cạnh, góc và đường chéo của hình bình hành.

Dạng 2. Chứng minh tứ giác là hình bình hành

Phương pháp giải: Áp dụng các dấu hiệu nhận biết của hình bình hành

a) Tứ giác có các cạnh đối song song là hình bình hành;

b) Tứ giác có các cạnh đối bằng nhau là hình bình hành;

c) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành;

d) Tứ giác có các góc đối bằng nhau là hình bình hành;

e) Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.

Xem thêm các bài viết liên quan hay, chi tiết

Giải Toán 8 (Kết nối tri thức): Bài tập cuối chương 3 trang 74 

50 bài tập về hình bình hành (có đáp án 2024) – Toán 8