Câu hỏi:
19/07/2024 157Cho mặt cầu . Tìm các điểm sao cho khoảng cách từ điểm M đến mặt phẳng là lớn nhất, khoảng cách từ điểm N đến mặt phẳng là nhỏ nhất, với .
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Mặt cầu có tâm , bán kính .
Ta làm theo hai cách.
Ta có: nên .
Do đó mặt phẳng không có điểm chung với mặt cầu .
Tất cả các điểm thuộc mặt cầu đều nằm trong miền giới hạn bởi hai mặt phẳng song song với và tiếp xúc với mặt cầu, nên điểm có khoảng cách lớn nhất, nhỏ nhất là các giao điểm của đường thẳng Δ với mặt cầu , với là đường thẳng qua I và vuông góc với .
Phương trình đường thẳng .
Gọi .
Ta có nên .
Suy ra hai điểm thỏa mãn .
Khoảng cách từ các điểm đến là
Vậy các điểm cần tìm là .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số có bảng xét dấu của đạo hàm như sau:

Hàm số đồng biến trên khoảng nào dưới đây?
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có cạnh , . Hai mặt bên và cùng vuông góc với mặt phẳng đáy , cạnh . Tính theo a thể tích V của khối chóp S.ABCD.
Câu 3:
Cho hàm số . Hàm số có đồ thị như sau:
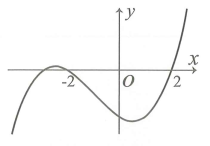
Bất phương trình nghiệm đúng với mọi khi và chỉ khi
Câu 6:
Trong không gian với hệ tọa độ Oxyz, viết phương trình đường vuông góc chung của hai đường thẳng và .
Câu 7:
Tích tất cả các số thực m để hàm số có giá trị nhỏ nhất trên đoạn bằng 18 là
Câu 8:
Cho hàm số có đồ thị như hình bên dưới.
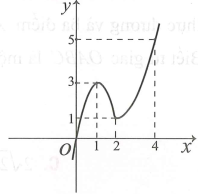
Có bao nhiêu giá trị nguyên của tham số m để phương trình có nghiệm?
Câu 9:
Gọi S là diện tích hình phẳng giới hạn bởi các đường , trục hoành và 2 đường thẳng trong hình vẽ bên.
Đặt: . Mệnh đề nào sau đây đúng
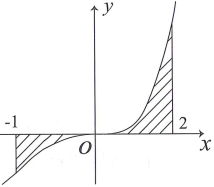
Câu 11:
Cho mặt cầu có diện tích đường tròn lớn là 2π. Khi đó, mặt cầu có bán kính là:
Câu 13:
Cho hàm số có đạo hàm xác định trên và thỏa mãn và . Số nghiệm nguyên dương của bất phương trình là
Câu 15:
Cho x, y là các số dương thỏa mãn . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của . Tính .



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)