Câu hỏi:
06/11/2024 536Cho khối cầu có bán kính R = 2. Thể tích của khối cầu đã cho là
A. 32π3
B. 256π
C. 64π
D. 16π
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Lời giải:
Thể tích khối cầu bán kính R=2 là: V = 4/3. π. 23
*Phương pháp giải:
Khối cầu bán kính r có thể tích là V =
Tính chất của mặt cầu
Nếu điểm ngoài mặt cầu thì:
- Qua có vô số tiếp tuyến với mặt cầu.
- Độ dài các đoạn thẳng nối với các tiếp điểm đều bằng nhau.
- Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.
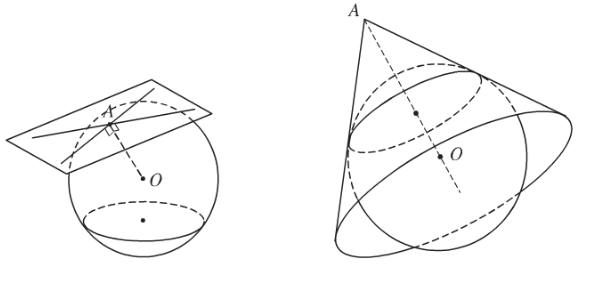
3. Vị trí tương đối của mặt cầu với đường thẳng
Cho mặt cầu tâm , bán kính và đường thẳng , gọi là hình chiếu của trên .
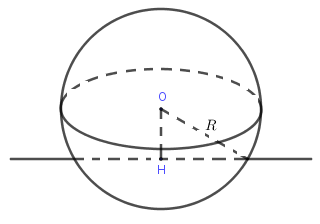
+ Nếu thì cắt tại điểm phân biệt.
+ Nếu thì cắt tại một điểm duy nhất . ( là tiếp tuyến với mặt cầu, là tiếp điểm)
+ Nếu thì và không có điểm chung.
Vị trí tương đối của mặt cầu với mặt phẳng
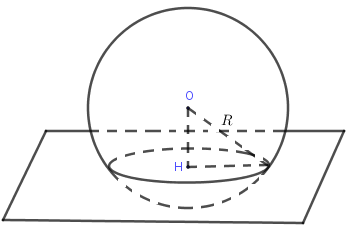
Cho mặt cầu tâm , bán kính và mặt phẳng , gọi là hình chiếu của trên .
+ Nếu thì cắt theo đường tròn tâm và bán kình .
+ Nếu thì tiếp xúc tại tiếp điểm .
+ Nếu thì và không có điểm chung.
Đặc biệt: Nếu thì đường tròn giao tuyến của và được gọi là đường tròn lớn, được gọi là mặt phẳng kính.
Công thức tính diện tích mặt cầu, thể tích khối cầu
1. Công thức tính diện tích mặt cầu
- Cho mặt cầu (S) có bán kính r.
Khi đó diện tích mặt cầu
- Chú ý: Diện tích S của mặt cầu bán kính r bằng bốn lần diện tích hình tròn lớn của mặt cầu đó.
2. Công thức tính thể tích khối cầu
Khối cầu bán kính r có thể tích là V =
Các dạng bài về mặt cầu và cách giải
Dạng 1. Xác định tâm và bán kính mặt cầu ngoại tiếp hình lăng trụ đứng
Ta xác định tâm O và O' của hai đáy
Tâm của mặt cầu ngoại tiếp lăng trụ lúc này chính là trung điểm của OO'
R = IA =
Chú ý: Hình lăng trụ nội tiếp trong một mặt cầu khi nó là hình lăng trụ đứng và có đáy đa giác nội tiếp.
Mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' có:
- Tâm là trung điểm AC'
- Bán kính R = =
Khi ABCD.A'B'C'D là hình lập phương: R =
Dạng 2. Mặt cầu ngoại tiếp hình chóp
Để xác định tâm của mặt cầu ngoại tiếp hình chóp, chúng ta thực hiện theo các bước sau:
- Tìm tâm O của mặt đáy
+ Trong tam giác đều: Giao điểm của 3 đường trung tuyến
+ Hình vuông và hình chữ nhật: Giao điểm 2 đường chéo
+ Tam giác vuông: Trung điểm của cạnh huyền
- Dựng một trục d là đường thẳng đi qua O và vuông góc với đáy (d song song với chiều cao hình chóp)
- Ta sẽ xác định mặt phẳng trung trực (P) của một cạnh bên
- Giao điểm của mặt phẳng (P) và d là tâm của mặt cầu ngoại tiếp
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số f(x) = ax3+bx2+cx+d có đồ thị là đường cong như hình vẽ. Tính tổng S=a+b+c+d.
Câu 2:
Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn . Biết f(0)=1 và , khi đó giá trị của f(1) bằng
Câu 3:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số nghịch biến trên R. Số phần tử của S là
Câu 4:
Cho hình chữ nhật ABCD có . Quay hình chữ nhật này xung quanh cạnh AD. Diện tích xung quanh của hình trụ được tạo thành là
Câu 5:
Cho hàm số y = f(x) liên tục trên đoạn [-1;3] và có đồ thị như hình vẽ bên. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn [-1;3]. Giá trị của M-m bằng
Câu 6:
Cho hàm số f(x) xác định trên R\{-1;5} và có bảng biến thiên như sau:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2019;2019] để phương trình có nghiệm?
Câu 7:
Đầu tháng một người gửi ngân hàng 400.000.000 đồng (400 triệu đồng) với lãi suất gửi là 0,6% mỗi tháng theo hình thức lãi suất kép. Cuối mỗi tháng người đó đều đặn gửi vào ngân hàng số tiền là 10.000.000 (10 triệu đồng). Hỏi sau ít nhất bao nhiêu tháng (kể từ lúc người này ra ngân hàng gửi tiền) thì số tiền người đó tích lũy được lớn hơn 700.000.000 (bảy trăm triệu đồng)?
Câu 9:
Xét các số thực dương a, b, x, y thỏa mãn a>1, b>1 và . Giá trị nhỏ nhất của biểu thức P=3x+4y thuộc tập hợp nào dưới đây?
Câu 11:
Trong mặt phẳng cho tập hợp P gồm 10 điểm phân biệt trong đó không có 3 điểm nào thẳng hàng. Số tam giác có 3 đỉnh đều thuộc tập hợp P là
Câu 12:
Hàm số nào trong các hàm số sau đây có đồ thị phù hợp với hình bên?
Câu 13:
Trong không gian cho tam giác ABC vuông tại A có và . Khi quay tam giác ABC xung quanh cạnh AC thì đường gấp khúc ACB tạo thành một hình nón. Diện tích toàn phần của hình nón đó bằng
Câu 14:
Trong không gian Oxyz, cho hai điểm A(2;4;1), B(-1;1;3) và mặt phẳng . Mặt phẳng (β) đi qua hai điểm A, B và vuông góc với mặt phẳng (α) có dạng . Giá trị a-b+c bằng
Câu 15:
Có bao nhiêu tiếp tuyến của đồ thị hàm số y = x3-x2+x+1 song song với đường thẳng y=6x+4?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)