Câu hỏi:
15/07/2024 148Cho hàm số là tham số thực). Gọi S là tập hợp tất cả các giá trị nguyên sao cho . Số phần S là:
A. 9
B. 10
C. 11
D. 12
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Xét hàm số , hàm số liên tục trên đoạn [1;2].
Ta có: Hàm số f(x) đồng biến trên đoạn [1;2], do đó .
TH1: thì .
Khi đó:
trường hợp này có 9 số nguyên.
TH2: thì .
Khi đó:
trường hợp này có 2 số nguyên.
TH3: thì
Do m là số nguyên nên:
không tồn tại thỏa mãn.
Vậy số phần tử của tập S là 11.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho các điểm A(1;4;5), B(0;3;1), C(2;-1;0) và mặt phẳng (P): 3x - 3y - 2z - 15 = 0. Gọi M(a;b;c) là điểm thuộc (P) sao cho tổng các bình phương khoảng cách từ M đến A, B, C nhỏ nhất. Tính a + b + c.
Câu 2:
Cho hàm số y = f(x) có bảng biến thiên như sau
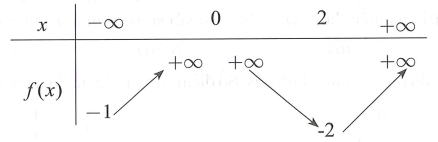
Tập hợp tất cả các giá trị thực của tham số m để phương trình f(x) + m = 0 có hai nghiệm phân biệt là
Câu 3:
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10;10] để hàm số nghịch biến trên khoảng (1;2)?
Câu 4:
Cho hàm số có đồ thị như hình dưới đây. Số điểm cực trị của đồ thị hàm số là
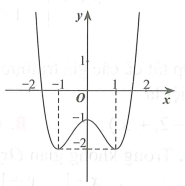
Câu 6:
Cho hình chóp S.ABC có đường cao SA, tam giác ABC vuông tại A có AB = 2, AC = 4. Gọi H là trung điểm của BC. Biết diện tích tam giác SAH bằng 2, thể tích của khối chóp S.ABC bằng
Câu 8:
Cho hàm số y = f(x) có đồ thị như hình dưới đây. Diện tích của hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục Ox là:
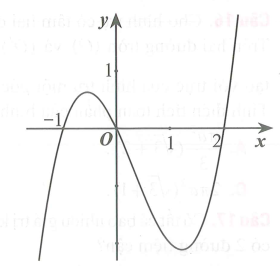
Câu 9:
Biết số phức z = -3 + 4i là một nghiệm của phương trình , trong đó a, b là các số thực. Tính a - b.
Câu 10:
Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác cân tại A có Biết thể tích khối chóp S.ABC bằng góc giữa hai mặt phẳng (SBC) và (ABC) bằng
Câu 11:
Thể tích của khối trụ tròn xoay có bán kính đáy và chiều cao đều bằng 5 là:
Câu 12:
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau. Biết SA = 3, SB = 4, SC = 5 thể tích khối chóp S.ABC bằng
Câu 13:
Trong không gian Oxyz, khoảng cách từ gốc tọa độ (O) đến mặt phẳng (P): x - y + 2z = 0 bằng
Câu 15:
Có bao nhiêu cách chọn ra một tổ trưởng và một tổ phó từ một tổ có 10 người? Biết khả năng được chọn của mỗi người trong tổ là như nhau.



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)