Câu hỏi:
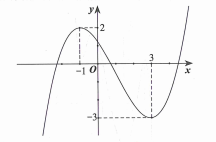
17/07/2024 228Cho hàm số y = f(x) có đồ thị được cho như hình vẽ bên dưới. Hỏi phương trình |f(x3−3x+1)−2|=1 có tất cả bao nhiêu nghiệm thực phân biệt?
A. 8
B. 6
C. 9
D. 11
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Cách 1: Phương pháp tự luận truyền thống
- Dựa vào đồ thị hàm số , ta có: |f(x3−3x+1)−2|=1⇔[f(x3−3x+1)=1f(x3−3x+1)=3
⇔[[x3−3x+1=b (b<−1) (2)x3−3x+1=c (−1<c<3) (3)x3−3x+1=d (d>3) (4)x2−3x+1=a (a>d) (1)
Dựa vào đồ thị hàm số y=x3−3x+1 (hình vẽ bên đây)
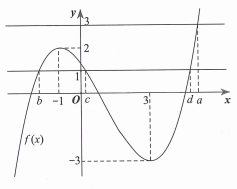
Ta suy ra: Phương trình (1), (2), (4) mỗi phương trình có 1 nghiệm, phương trình (3) có 3 nghiệm và các nghiệm này đều phân biệt.
Vậy phương trình đã cho có 6 nghiệm phân biệt.
Cách 2: Phương pháp ghép trục
Đặt u=x3−3x+1
Ta có u'
Bảng biến thiên của hàm số :
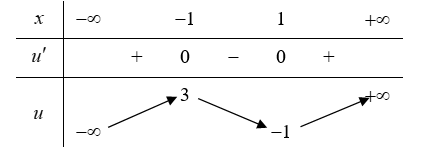
Phương trình trở thành:
Từ đồ thị hàm số y = f(x) và từ bảng biến thiên của hàm số ta có bảng biến thiên của hàm hợp như sau:
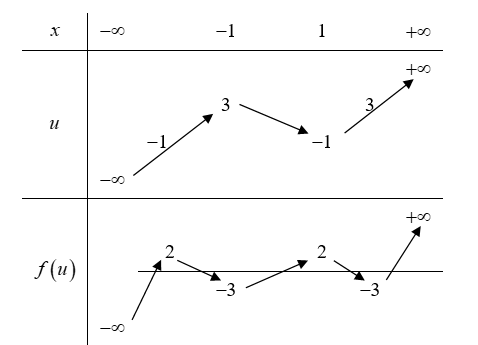
Từ bảng trên ta thấy phương trình f(u) = 1 có 5 nghiệm và phương trình f(u) = 3 có 1 nghiệm.
Vậy phương trình đã cho có 6 nghiệm.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tập hợp S tất cả các giá trị của tham số thực m để hàm số nghịch biến trên khoảng (-1;1).
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông, AB = 1, cạnh bên SA = 1 và vuông góc với mặt phẳng đáy (ABCD). Kí hiệu M là điểm di động trên đoạn CD và N là điểm di động trên đoạn CB sao cho . Thể tích nhỏ nhất của khối chóp S.AMN là?
Câu 3:
Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và BC. Số đo của góc (IJ,CD) bằng:
Câu 4:
Cho hàm số f(x) liên tục trên R, diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b (với a < b) được tính theo công thức
Câu 5:
Trong không gian Oxyz, cho bốn đường thẳng: , , , . Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là
Câu 6:
Cho hàm số f(x) có đạo hàm, liên tục trên đoạn [0;1] và thỏa mãn các điều kiện f(1) = 0 và . Tính tích phân bằng
Câu 7:
Cho hàm số . Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho . Số phần tử của S là:
Câu 8:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB vuông tại S và nằm trong mặt phẳng vuông góc với đáy. Hình chiếu vuông góc của S trên AB là điểm H thỏa mãn AH = 2BH. Tính theo a thể tích V của khối chóp S.ABCD.
Câu 9:
Xét hàm số y = f(x) với có bảng biến thiên như sau:
Khẳng định nào sai đây là đúng
![Xét hàm số f(x) với x thuộc đoạn [-1;5] có bảng biến thiên như sau: Khẳng định nào sai đây là đúng (ảnh 1)](https://vietjack.me/storage/uploads/images/233/zx16-1650184383.png)
Câu 10:
Trên mặt phẳng Oxy ta xét một hình chữ nhật ABCD với các điểm A(-2;0), B(-2;2), C(4;2), D(4;0). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm M(x;y) mà x + y < 2.
Câu 12:
Cho hàm số y = f(x) có bảng biến thiên như sau:
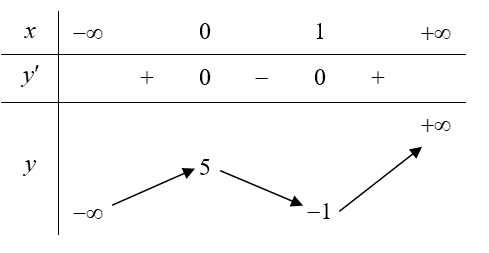
Hàm số đồng biến trên khoảng nào dưới đây?
Câu 13:
Cho hàm số f(x) liên tục trên đoạn [-1;4] và có đồ thị trên đoạn [-1;4] như hình vẽ bên.
Tích phân bằng
![Cho hàm số f(x) liên tục trên đoạn [-1;4] và có đồ thị trên đoạn [-1;4] như hình vẽ bên (ảnh 1)](https://vietjack.me/storage/uploads/images/233/106-1650139845.png)
Câu 14:
Cho khối nón có độ dài đường sinh bằng 2a và bán kính đáy bầng. Thể tích của khối nón đã cho bằng
Câu 15:
Biết thể tích khí năm 1998 là . 10 năm tiếp theo, thể tích tăng , 10 năm tiếp theo nữa, thể tích tăng n%. Thể tích năm 2016 là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)