Câu hỏi:
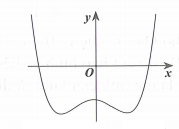
08/11/2024 975Cho hàm số y=ax4+bx2+c (a≠0) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng
A. a>0, b>0, c<0
B. a<0, b>0, c<0
C. a>0, b<0, c<0
D. a>0, b>0, c>0
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng:C
*Lời giải:
Quan sát đồ thị có bề lõm quay lên trên Þ a > 0
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm Þ c < 0
Hàm số có 3 cực trị Þa.b < 0 mà a > 0 nên Þ b < 0
*Phương pháp giải:
Nhận dạng đồ thị hàm bậc 4 trùng phương: y = ax4 + bx2 + c
+) Đạo hàm: 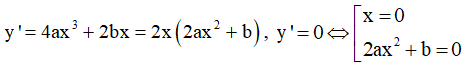
* Các lý thuyết thêm và các dạng bài toán về nhận diện đồ thị hàm số:
1.Nhận dạng đồ thị hàm số bậc 3: y = ax3 + bx2 + cx + d
a > 0
a < 0
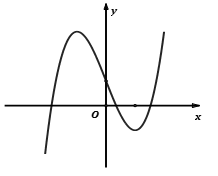
y' = 0 có hai nghiệm phân biệt hay Δy > 0
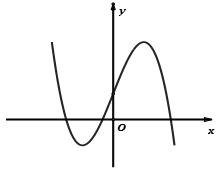
y' = 0 có nghiệm kép hay Δy = 0
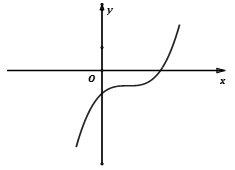
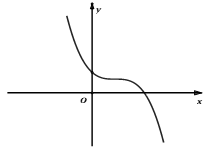
y' = 0 vô nghiệm hay Δy < 0
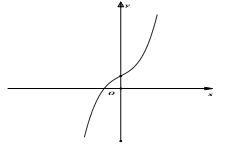
Hệ số a
Đồ thị hướng lên
a > 0
Đồ thị hướng xuống
a < 0
Hệ số b
Điểm uốn "lệch phải" so với Oy hoặc 2 điểm cực trị lệch phải so với Oy
ab < 0
Điểm uốn "lệch trái" so với Oy hoặc hai điểm cực trị "lệch trái" so với Oy
ab > 0
Điểm uốn thuộc Oy hoặc hai điểm cực trị cách đều trục Oy
b = 0
Hệ số c
Không có cực trị
c = 0
hoặc ac > 0
Hai điểm cực trị nằm về hai phía trục tung Oy
ac < 0
Có 1 điểm cực trị nằm trên Oy
c = 0
Hệ số d
Giao điểm với trục tung nằm trên điểm O
d > 0
Giao điểm với trục tung nằm dưới điểm O
d < 0
Giao điểm với trục tung trùng điểm O
d = 0
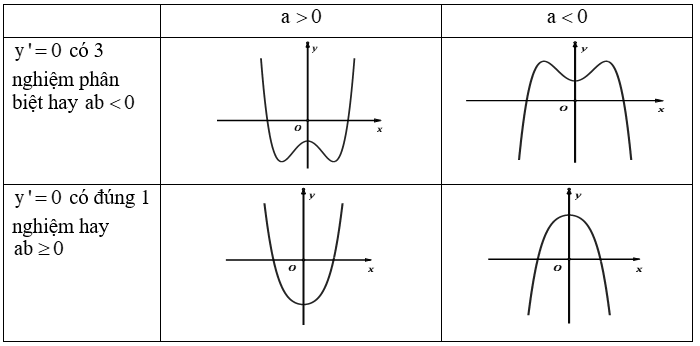
2. Nhận dạng đồ thị hàm bậc 4 trùng phương: y = ax4 + bx2 + c
+) Đạo hàm: 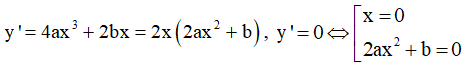

Hệ số a
Đồ thị có bề lõm hướng lên
a > 0
Đồ thị có bề lõm hướng xuống
a < 0
Hệ số b
Đồ thị hàm số có 3 điểm cực trị
ab < 0
Đồ thị hàm số chỉ có 1 điểm cực trị (Đang xét a ≠ 0)
ab ≥ 0
Hệ số c
Giao điểm với trục tung nằm trên điểm O
c > 0
Giao điểm với trục tung nằm dưới điểm O
c < 0
Giao điểm với trục tung trùng điểm O
c=0
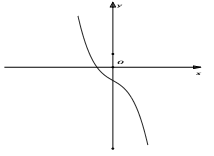
3. Nhận dạng đồ thị hàm số 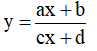
+ Tập xác định: 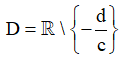
+ Đạo hàm: 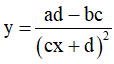
+ Đồ thị hàm số có: 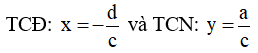
+ Đồ thị có tâm đối xứng: 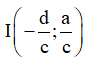
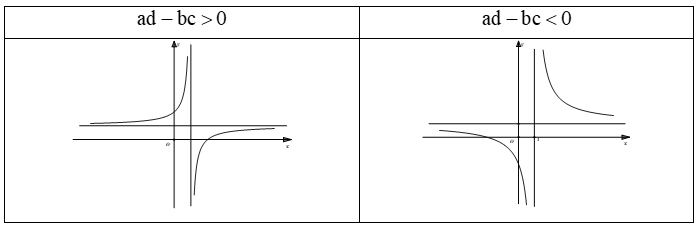
Tiêu chí nhận dạng:
- Dựa vào tiệm cận đứng + tiệm cận ngang.
- Dựa vào giao Ox,Oy
- Dựa vào sự đồng biến, nghịch biến.
ab
Giao Ox nằm phía "phải" điểm O
ab < 0
Giao Ox nằm phía "trái" điểm O
ab > 0
Không cắt Ox
a = 0
ac
Tiệm cận ngang nằm "phía trên" Ox
ac > 0
Tiệm cận ngang nằm "phía dưới" Ox
ac < 0
Tiệm cận ngang trùng Ox
a = 0
bd
Giao Oy nằm trên điểm O
bd > 0
Giao Oy nằm dưới điểm O
bd < 0
Giao Oy trùng gốc tọa độ O
b = 0
cd
Tiệm cận đứng nằm "bên phải" Oy
cd < 0
Tiệm cận đứng nằm "bên trái" Oy
cd > 0
Tiệm cận đứng trùng Oy
d = 0
4. Lưu ý:
- Tại giao điểm với trục Ox thì thay y = 0 và biện luận.
- Tại giao điểm với trục Oy thì thay x = 0 và biện luận.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Ôn tập chương 1 (mới 2024 + Bài Tập) – Toán 12
50 bài tập về nhận dạng đồ thị hàm số (có đáp án 2024) – Toán 12
Quan sát đồ thị có bề lõm quay lên trên Þ a > 0
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm Þ c < 0
Hàm số có 3 cực trị Þa.b < 0 mà a > 0 nên Þ b < 0*Phương pháp giải:
Nhận dạng đồ thị hàm bậc 4 trùng phương: y = ax4 + bx2 + c
+) Đạo hàm: 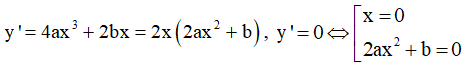

* Các lý thuyết thêm và các dạng bài toán về nhận diện đồ thị hàm số:
1.Nhận dạng đồ thị hàm số bậc 3: y = ax3 + bx2 + cx + d
|
|
a > 0 |
a < 0 |
|
y' = 0 có hai nghiệm phân biệt hay Δy > 0 |
|
|
|
y' = 0 có nghiệm kép hay Δy = 0 |
|
|
|
y' = 0 vô nghiệm hay Δy < 0 |
|
|
|
Hệ số a |
Đồ thị hướng lên |
a > 0 |
|
Đồ thị hướng xuống |
a < 0 |
|
|
Hệ số b |
Điểm uốn "lệch phải" so với Oy hoặc 2 điểm cực trị lệch phải so với Oy |
ab < 0 |
|
Điểm uốn "lệch trái" so với Oy hoặc hai điểm cực trị "lệch trái" so với Oy |
ab > 0 |
|
|
Điểm uốn thuộc Oy hoặc hai điểm cực trị cách đều trục Oy |
b = 0 |
|
|
Hệ số c |
Không có cực trị |
c = 0 hoặc ac > 0 |
|
Hai điểm cực trị nằm về hai phía trục tung Oy |
ac < 0 |
|
|
Có 1 điểm cực trị nằm trên Oy |
c = 0 |
|
|
Hệ số d |
Giao điểm với trục tung nằm trên điểm O |
d > 0 |
|
Giao điểm với trục tung nằm dưới điểm O |
d < 0 |
|
|
Giao điểm với trục tung trùng điểm O |
d = 0 |
2. Nhận dạng đồ thị hàm bậc 4 trùng phương: y = ax4 + bx2 + c
+) Đạo hàm: 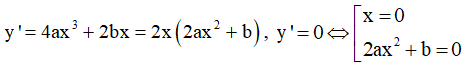

|
Hệ số a |
Đồ thị có bề lõm hướng lên |
a > 0 |
|
Đồ thị có bề lõm hướng xuống |
a < 0 |
|
|
Hệ số b |
Đồ thị hàm số có 3 điểm cực trị |
ab < 0 |
|
Đồ thị hàm số chỉ có 1 điểm cực trị (Đang xét a ≠ 0) |
ab ≥ 0 |
|
|
Hệ số c |
Giao điểm với trục tung nằm trên điểm O |
c > 0 |
|
Giao điểm với trục tung nằm dưới điểm O |
c < 0 |
|
|
Giao điểm với trục tung trùng điểm O |
c=0 |
3. Nhận dạng đồ thị hàm số 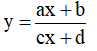
+ Tập xác định: 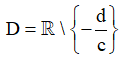
+ Đạo hàm: 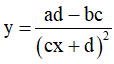
+ Đồ thị hàm số có: 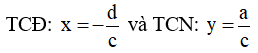
+ Đồ thị có tâm đối xứng: 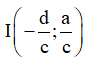

Tiêu chí nhận dạng:
- Dựa vào tiệm cận đứng + tiệm cận ngang.
- Dựa vào giao Ox,Oy
- Dựa vào sự đồng biến, nghịch biến.
|
ab |
Giao Ox nằm phía "phải" điểm O |
ab < 0 |
|
Giao Ox nằm phía "trái" điểm O |
ab > 0 |
|
|
Không cắt Ox |
a = 0 |
|
|
ac |
Tiệm cận ngang nằm "phía trên" Ox |
ac > 0 |
|
Tiệm cận ngang nằm "phía dưới" Ox |
ac < 0 |
|
|
Tiệm cận ngang trùng Ox |
a = 0 |
|
|
bd |
Giao Oy nằm trên điểm O |
bd > 0 |
|
Giao Oy nằm dưới điểm O |
bd < 0 |
|
|
Giao Oy trùng gốc tọa độ O |
b = 0 |
|
|
cd |
Tiệm cận đứng nằm "bên phải" Oy |
cd < 0 |
|
Tiệm cận đứng nằm "bên trái" Oy |
cd > 0 |
|
|
Tiệm cận đứng trùng Oy |
d = 0 |
4. Lưu ý:
- Tại giao điểm với trục Ox thì thay y = 0 và biện luận.
- Tại giao điểm với trục Oy thì thay x = 0 và biện luận.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Ôn tập chương 1 (mới 2024 + Bài Tập) – Toán 12
50 bài tập về nhận dạng đồ thị hàm số (có đáp án 2024) – Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong không gian Oxyz, cho điểm A(1;-3;2). Gọi M, N, P lần lượt là hình chiếu vuông góc của A lên trục Ox, Oy, Oz. Phương trình mặt phẳng (MNP) là
Câu 2:
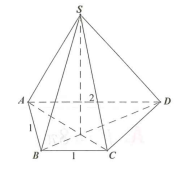
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; AB = BC = 1, AD = 2. Các mặt chéo (SAC) và (SBD) cùng vuông góc với mặt đáy (ABCD). Biết góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 60° (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng (SAB) là
Câu 3:
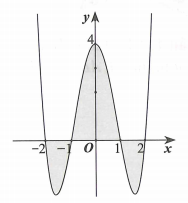
Cho hàm số bậc hai y=f(x)=x4−5x2+4 có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề nào sau đây sai?
Câu 4:
Trong không gian Oxyz, cho đường thẳng d:x−21=y−42=z−52 và mặt phẳng (P):2x+z−5=0. Đường thẳng nằm trong mặt phẳng (P), cắt và vuông góc với đường thẳng d có phương trình là
Câu 5:
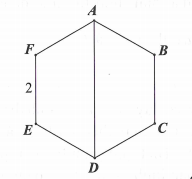
Cho hình lục giác đều ABCDEF có cạnh bằng 2 (tham khảo hình vẽ). Quay lục giác xung quanh đường chéo AD ta được một khối tròn xoay. Thể tích khối tròn xoay đó là
Câu 6:
Trong không gian Oxyz, cho hai điểm A(1;1;3), B(5;2;-1) và hai điểm M, N thay đổi trên mặt phẳng (Oxy) sao cho điểm I(1;2;0) luôn là trung điểm của MN. Khi biểu thức P=MA2+2NB2+¯MA.¯NB đạt giá trị nhỏ nhất. Tính T=2xM−4xN+7yM−yN.
Câu 8:
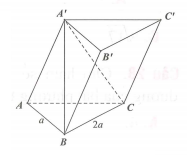
Cho khối lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB = a, BC = 2a, A'B vuông góc với mặt phẳng (ABC) và góc giữa A'C và mặt phẳng (ABC) bằng 30° (tham khảo hình vẽ bên). Tính thể tích khối lăng trụ ABC.A'B'C'.
Câu 10:
Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a.
Câu 11:
Trong không gian Oxyz, cho đường thẳng d:x−12=y−1=z−21 và mặt phẳng (P):x+y+2z−1=0. Góc giữa đường thẳng d và mặt phẳng (P) bằng
Câu 12:
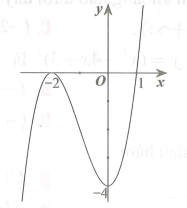
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ. Tọa độ điểm cực tiểu của (C) là
Câu 13:
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ bên
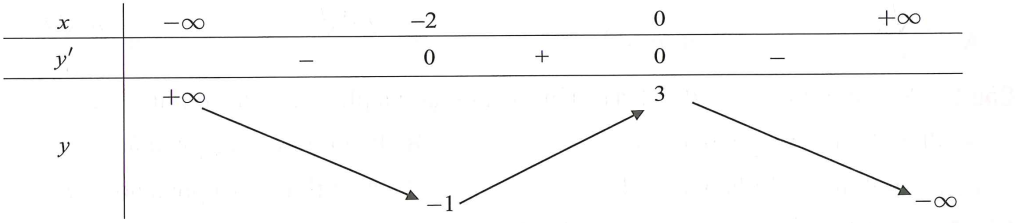
Hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
Câu 14:
Trong không gian Oxyz, cho hai véc tơ →a=(−4;5;−3) và →b=(2;−2;3). Véc tơ →x=→a+2→b có tọa độ là



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)