Câu hỏi:
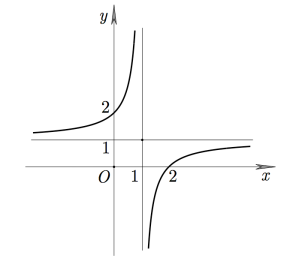
22/07/2024 156Cho (H) là hình phẳng nằm bên trong nửa elip y=12√4-x2 và nằm bên ngoài parabol y=√32x2. Diện tích của (H) bằng
A. 4π-√36
B. 2π+√36
C. 2π-√36
D. 4π+√36
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Cho các số thực dương a1,a2,a3,a4,a5 theo thứ tự lập thành cấp số cộng và các số thực dương b1,b2,b3,b4,b5 theo thứ tự lập thành cấp số nhân. Biết rằng a1=b1 và a5=17617b5. Giá trị nhỏ nhất của biểu thức a2+a3+a4b2+b3+b4 bằng
Câu 3:
Cho khối tứ diện ABCD có AB=x,AC=AD=CB=DB=2√3, khoảng cách giữa AB,CD bằng 1. Tìm x, để khối tứ diện ABCD có thể tích lớn nhất.
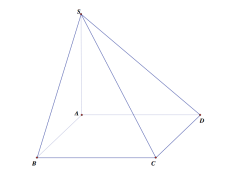
Câu 4:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a,SA=a vuông góc với đáy. Côsin góc giữa đường thẳng SC và mặt phẳng (SBD) bằng
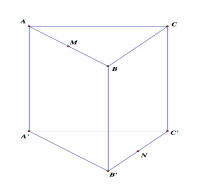
Câu 6:
Cho hình lăng trụ tam giác đều ABC.A′B′C′ có tất cả các cạnh bằng a. Gọi M,N lần lượt là trung điểm các cạnh AB,B′C′ (tham khảo hình vẽ bên). Côsin góc giữa hai đường thẳng MN và AC bằng
Câu 7:
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(1;2;3), B(3;4;5) và mặt phẳng (α):x+2y+3z-14=0. Gọi Δ là đường thẳng thay đổi nằm trong mặt phẳng (α), các điểm M,N lần lượt là hình chiếu vuông góc của A,B trên Δ. Biết rằng khi AM = BN thì trung điểm của MN luôn thuộc một đường thẳng cố định. Viết phương trình đường thẳng cố định đó.
Câu 9:
Có bao nhiêu số nguyên m < 10 để hàm số y=|x3-mx+1| có 5 điểm cực trị.
Câu 10:
Cho ∫e1lnx(lnx+x+1)2dx=ae-2be+4, với a,b là các số nguyên dương. Giá trị của biểu thức b-a bằng
Câu 11:
Xét tập (A) gồm các số phức z thoả mãn z-2iz-2 là số thuần ảo và các giá trị thực m,n sao cho chỉ có duy nhất một số phức z∈(A) thoả mãn |z-m-ni|=√2. Đặt M=max( m+n) và N=min( m+n). Tính P=M+N.
Câu 12:
Thể tích của khối tứ diện OABC có OA=OB=OC=a và OA,OB,OC đôi một tạo với nhau một góc 60° bằng



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)