Cho đa giác đều 20 đỉnh nội tiếp đường tròn tâm O. Chọn ngẫu nhiên 4 đỉnh của đa giác đó. Tính xác suất sao cho 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật.

Đáp án đúng: B

* Lời giải:

* Phương pháp giải:

Tìm số phần tử không gian mẫu

- Tìm số phần tử thuận lợi của biến cố A đã cho

- Tính xác suất 

* Lý thuyết nắm thêm

1. Quy tắc cộng

- Quy tắc cộng: Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động này có m cách thực hiện, hành động kia có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.

- Quy tắc cộng được phát biểu ở trên thực chất là quy tắc đếm số phần tử của hợp hai tập hợp hữu hạn không giao nhau, được phát biểu như sau:

Nếu A và B là các tập hợp hữu hạn và không giao nhau thì:

$n(A\cup B)=n\left(A\right)+n\left(B\right)$

- Chú ý: Quy tắc cộng có thể mở rộng cho nhiều hành động.

2. Quy tắc nhân

- Quy tắc nhân: Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có m.n cách hoàn thành công việc.

- Chú ý: Quy tắc nhân có thể mở rộng cho nhiều hành động liên liếp.

3. Hoán vị

3.1 Định nghĩa

- Định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.

- Nhận xét: Hai hoán vị của n phần tử khác nhau ở thứ tự sắp xếp.

Chẳng hạn, hai hoán vị abc và cab của ba phần tử a; b; c là khác nhau.

3.2 Số các hoán vị

Kí hiệu: P_n là số các hoán vị của n phần tử.

- Định lí: P_n = n.(n – 1).(n – 2)….2.1

- Chú ý: Kí hiệu n.(n – 1)…2.1 là n! (đọc là n là giai thừa), ta có: P_n = n!.

4. Chỉnh hợp

4.1 Định nghĩa.

- Cho tập hợp A gồm n phần tử (n ≥ 1).

Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

4.2 Số các chỉnh hợp

- Kí hiệu $A_n^k$ là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) .

- Định lí:

$A_n^k=n(n-1)\mathrm{...}(n-k+\text{\hspace{0.17em}}1)$

5. Tổ hợp

5.1 Định nghĩa.

- Giả sử tập A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.

- Chú ý: Số k trong định nghĩa cần thỏa mãn điều kiện 1 ≤ k ≤ n. Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tổ hợp chập 0 của n phần tử là tập rỗng.

- Ví dụ 4. Cho tập A = {3; 4; 5; 6}.

Ta liệt kê các tổ hợp chập 3 của A là: {3; 4; 5}; {3; 4; 6}; {3; 5; 6}; {4; 5; 6}.

5.2 Số các tổ hợp.

Kí hiệu $C_n^k$ là số các tổ hợp chập k của n phần tử ( 0 ≤ k ≤ n).

- Định lí: $C_n^k=\frac{n!}{k!(n-k)!}$.

5.3 Tính chất của các số $C_n^k$

a) Tính chất 1.

$C_n^k=C_n^{n-k};0\le k\le n$

Ví dụ 7. $C_8^4+C_8^5=C_9^5=126$.

6. Công thức nhị thức Niu- tơn

Ta có:

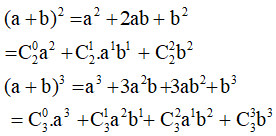
- Công thức nhị thức Niu – tơn.

$$\begin{gathered} {(a\text{\hspace{0.17em}\hspace{0.17em}}+b)}^n=C_n^0{a}^n+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^1.a^{n-1}b \\ +\text{\hspace{0.17em}}\mathrm{...}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^k.a^{n-k}{b}^k\text{\hspace{0.17em}}+\text{}\mathrm{....}+ \\ \text{}{C}_n^{n-1}a{b}^{n-1}+\text{\hspace{0.17em}\hspace{0.17em}}{C}_n^n{b}^n \end{gathered}$$

- Hệ quả:

Với a = b = 1 ta có: $2^n=C_n^0+\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}\text{}+\text{\hspace{0.17em}}{C}_n^n$

Với a = 1; b = – 1 ta có: $0=C_n^0-\text{\hspace{0.17em}}{C}_n^1+\text{}\mathrm{...}$$+\text{}{(-1)}^k.C_n^k+\text{}\mathrm{...}\text{}+{(-1)}^n\text{\hspace{0.17em}}{C}_n^n$

- Chú ý:

Trong biểu thức ở vế phải của công thức (1):

a) Số các hạng tử là n + 1.

b) Các hạng tử có số mũ của a giảm dần từ n đến 0; số mũ của b tăng dần từ 0 đến n, nhưng tổng các số mũ của a và b trong mỗi hạng tử luôn bằng n (quy ước $a^0=b^0=1$).

c) Các hệ số của mỗi cặp hạng tử cách đều hai hạng tử đầu và cuối thì bằng nhau.

Xem thêm các bài viết liên quan hay, chi tiết:

Chuyên đề Ôn tập chương 2: Tổ hợp - xác suất - Toán 11 

50 Bài tập Xác suất của biến cố Toán 11 mới nhất