Câu hỏi:
21/07/2024 88Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 3 đỉnh. Tính xác suất để 3 đỉnh đó là 3 đỉnh của một tam giác vuông không cân.
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
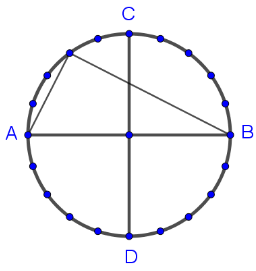
Để các tam giác đó là các tam giác vuông thì cạnh huyền của tam giác đó phải là đường kính của đường tròn.
Với mỗi đường kính của đường tròn (giả sử là AB), có thể nối với 16 đỉnh để tạo thành các tam giác vuông không cân (không nối với C và D) (hình vẽ).
Mà có tất cả 10 đường kính, như vậy số tam giác thỏa mãn đề bài là: 10*16=160.
Xác suất cần tính là .
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Đường tiệm cận xiên của đồ thị hàm số tạo với hai trục tọa độ một tam giác có diện tích bằng
Câu 3:
Cho tứ diện đều ABCD cạnh a. Tính diện tích mặt cầu nội tiếp tứ diện ABCD.
Câu 8:
Hình chóp S.ABC có đáy là tam giác vuông tại B có AB=a, AC=2a, SA vuông góc với mặt phẳng đáy, SA=2a. Gọi α là góc tạo bởi hai mặt phẳng (SAC) và (SBC). Tính .
Câu 9:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a; SA = 2a và vuông góc với đáy. Khoảng cách từ điểm A tới mặt phẳng (SBD) là
Câu 10:
Cho Tiếp tuyến của (C) song song với đường thẳng có phương trình là
Câu 12:
Số véctơ khác có điểm đầu và điểm cuối là hai trong 6 đỉnh của lục giác ABCDEF là
Câu 15:
Cho hàm số có đạo hàm Hỏi đồ thị hàm số có bao nhiêu điểm cực trị?



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)