Câu hỏi:
23/12/2024 355Cho các số thực x,y,z không âm thỏa mãn x + y + z = 2. GTLN và GTNN của biểu thức P=2√1+x+√1+y2+ lần lượt là M và m. Giá trị M + m nằm trong khoảng nào dưới đây?
A. (5;6)
B. (6;7)
C. (7;8)
D. (8;9)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là C
Lời giải
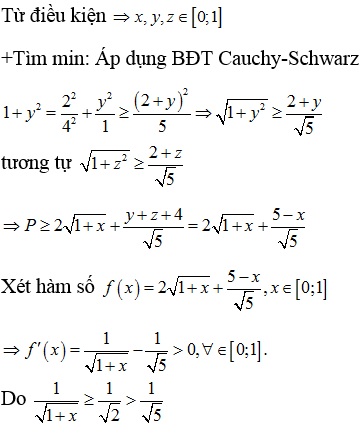
*Phương pháp giải:
Bước 1: Tìm các điểm x1; x2; …; xn thuộc khoảng (a; b) mà tại đó f'(x) bằng 0 hoặc không tồn tại.
Bước 2: Tính f(a); f(x1); f(x2); …; f(xn); f(b).
Bước 3: Gọi M là số lớn nhất và m là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó:
*Lý thuyết:
1. Định nghĩa
Cho hàm số y = f(x) xác định trên tập hợp D.
- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) ≤ M với mọi x thuộc D và tồn tại x0 thuộc D sao cho f(x0) = M. Kí hiệu
- Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) ≥ m với mọi x thuộc D và tồn tại x0 thuộc D sao cho f(x0) = m. Kí hiệu
Chú ý:
- Ta quy ước khi chỉ nói giá trị lớn nhất hay giá trị nhỏ nhất của hàm số y = f(x) (mà không cho rõ tập hợp D) thì ta hiểu đó là giá trị lớn nhất hay giá trị nhỏ nhất của hàm số y = f(x) trên tập xác định của nó.
- Giá trị lớn nhất và giá trị nhỏ nhất của hàm số thường được tìm bằng cách sử dụng đạo hàm và bảng biến thiên.
Xem thêm
TOP 40 câu Trắc nghiệm Giá trị lớn nhất, giá trị nhỏ nhất của hàm số (có đáp án 2024) - Toán 12
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Biết x1, x2 (x1<x2) là hai nghiệm của phương trình và với a,b là các số nguyên dương. Giá trị P=a+b là
Câu 2:
Trong không gian Oxyz, cho đường thẳng và mặt cầu (S): (x-2)2 + y2 + (z-1)2 =1. Gọi (P) và (Q) là ai mặt phẳng chứa đường thẳng (d) và tiếp xúc với mặt cầu (S) lần lượt tại M và N. Độ dài dây cung MN có giá trị bằng
Câu 3:
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M,N lần lượt là trung điểm của các cạnh A’B’ và BC. Mặt phẳng (DMN) chia hình lập phương thành 2 phần. Gọi V1 là thể tích của phần chứa đỉnh A, V2 là thể tích của phần còn lại. Tính tỷ số
Câu 4:
Cho tứ diện ABCD, gọi I, J lần lượt là trọng tâm các tam giác ABC và ABD. Khẳng định nào sau đây là sai?
Câu 5:
Gọi H là trực tâm của tam giác ABC. Phương trình các cạnh và đường cao của tam giác là AB: 7x-y+4=0; BH=2x+y-4=0; AH: x-y-2=0. Phương trình đường cao CH của tam giác ABC là
Câu 7:
Tìm giá trị của tham số m để đồ thị hàm số y=x4-2(m+1)x2+2m+3 có 3 điểm cực trị A,B,C là ba đỉnh của một tam giác, trục hoành chia tam gíac ABC thành một tam giác và một hình thang sao cho tỉ số diện tích tam giác nhỏ được chia ra và diện tích tam giác ABC bằng 4/9
Câu 8:
Trong không gian Oxyz, cho điểm M(1;1;2) và mặt phẳng (P): 2x-y+3z+1=0. Đường thẳng đi qua điểm M và vuông góc với mặt phẳng (P) có phương trình là
Câu 10:
Số lượng của một loài vi khuẩn trong phòng thí nghiệm được tính theo công thức S(t)=Aen, trong đó A là số lượng vi khuẩn ban đầu, S(t) là số lượng vi khuẩn có sau t (phút), r là tỷ lệ tăng trưởng (r>0), t (tính theo phút) là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu có 500 con và sau 5 giờ có 1500 con. Hỏi sau bao lâu, kể từ lúc bắt đầu, số lượng vi khuẩn đạt 121500 con?
Câu 11:
Cho hình chóp S.ABC có AB=2; AC=3; BC=4; SA=SB=SC=5 Góc giữa đường thẳng SA, BC gần với số nào nhất?
Câu 12:
Cho hai số thực dương x, y thỏa mãn Giá trị nhỏ nhất của P = 25x + y là
Câu 14:
Cho hình chóp S.ABC có Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu đi qua các điểm A,B,C,M,N
Câu 15:
Tìm hệ số của x5 trong khai triển P(x)=(1+x)+2(1+x)2+ … + 8(1+x)8



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)