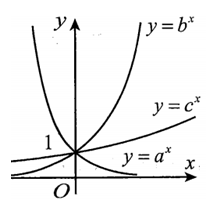
Cho ba số thực dương a; b; c khác 1. Đồ thị các hàm số $y=a^x;y=b^x;y=c^x$  được cho trong hình vẽ bên. Mệnh đề nào dưới đây đúng?

Cho số phức z thỏa mãn $\left(z-2-i\right)\left(\overline{z}-2-i\right)=25$ . Biết tập hợp các điểm M biểu diễn số phức $w=2\overline{z}-2+3i$  là đường tròn tâm $I\left(a;b\right)$ và bán kính c. Giá trị của  $a+b+c$ bằng:

Cho hình chóp S.ABCD đáy là hình thoi tâm O cạnh a, $\widehat{ABC}=60°,SA\perp \left(ABCD\right),SA=\frac{3a}{2}$ . Khoảng cách từ O đến mặt phẳng $\left(SBC\right)$   bằng:

Trong không gian Oxyz, cho hai điểm $A\left(3;-2;6\right),B\left(0;1;0\right)$  và mặt cầu $\left(S\right):{\left(x-1\right)}^2+{\left(y-2\right)}^2+{\left(z-3\right)}^2=25$ . Mặt phẳng $\left(P\right):ax+by+cz-2=0$  đi qua A, B và cắt mặt cầu theo giao tuyến $\left(S\right)$  là đường tròn có bán kính nhỏ nhất. Tính $T=a+b+c$ .

Cho hình lăng trụ đứng ABC.A’B’C’, đáy là tam giác ABC vuông tại $A,AB=a,\widehat{ABC}=30°$ , cạnh C’A hợp với mặt đáy góc $60°$ . Thể tích khối lăng trụ ABC.A’B’C’ là:

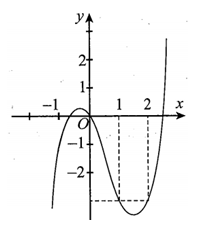
Cho hàm số $y=f\left(x\right)$  có đồ thị như hình bên và đạo hàm $f\text{'}\left(x\right)$  liên tục trên $\mathrm{ℝ}$ . Giá trị của biểu thức $\underset{1}{\overset{2}{\int }}f\text{'}\left(x\right)dx$  bằng:

Trong không gian Oxyz, cho hai điểm $M\left(1;2;0\right)$  và $N\left(5;-1;2\right)$ . Mặt phẳng trung trực của đoạn MN có phương trình là:

Cho $z=x+\left(x-1\right)i,x\in ℝ$ . Có bao nhiêu số thực x để $z^2$  là số thuần ảo?

Cho là các hàm số $f\left(x\right),g\left(x\right)$ xác định và liên tục trên $\mathrm{ℝ}$. Trong các mệnh đề sau, mệnh đề nào sai?

Đường thẳng nối hai điểm cực trị của đồ thị hàm số $y=\frac{m{x}^2+\left(4-2m\right)x-6}{2\left(x+9\right)}$  cách gốc tọa độ một khoảng lớn nhất khi m bằng:

Cho số phức $z=a+bi\left(a,b\in ℝ\right)$ . Số các mệnh đề đúng trong các mệnh đề sau là:

I. Môđun của z là một số thực dương.

II. $z^2={\left|z\right|}^2.$

III. $\left|\overline{z}\right|=\left|iz\right|=\left|z\right|$ .

IV. Điểm $M\left(-a;b\right)$  là điểm biểu diễn của số phức $\overline{z}$ .

Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây? 

Cho hình nón có thiết diện qua trục là một tam giác vuông cân cạnh huyền bằng 2a. Tính diện tích xung quanh  của hình nón.

Trong không gian Oxyz, hình chiếu vuông góc của điểm $M(2;3;1)$ trên đường Ox có tọa độ là:

Đồ thị hàm số $y=\frac{\sqrt{x^2+1}}{x-1}$  có bao nhiêu tiệm cận?

Gọi S là tập nghiệm của phương trình $9^x-{10.3}^x+9=0$. Tổng các phần tử của S bằng: