Câu hỏi:
20/07/2024 255
Cho ∆ABC cân tại A. Trên các cạnh AB, AC lần lượt lấy các điểm D và E sao cho AD = AE, CD cắt BE tại O. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC cân tại A. Trên các cạnh AB, AC lần lượt lấy các điểm D và E sao cho AD = AE, CD cắt BE tại O. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng nhất?
A. ∆BOC cân tại O;
A. ∆BOC cân tại O;
B. Ba điểm A, O, M thẳng hàng;
C. AM, BE, CD đồng quy tại một điểm;
D. Cả A, B, C đều đúng.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
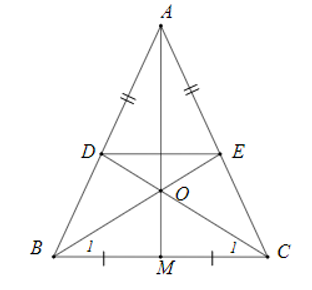
Ta có AB = AC (do ∆ABC cân tại A) và AD = AE (giả thiết).
Suy ra AB – AD = AC – AE.
Do đó BD = CE.
Xét ∆EBC và ∆DCB, có:
BC là cạnh chung.
(do ∆ABC cân tại A).
BD = CE (chứng minh trên).
Do đó ∆EBC = ∆DCB (c.g.c)
Suy ra (cặp góc tương ứng).
Suy ra ∆BOC cân tại O.
Do đó đáp án A đúng.
Ta có ∆BOC cân tại O.
Suy ra OB = OC.
Mà AB = AC (chứng minh trên)
Do đó AO là đường trung trực của cạnh BC (1).
Xét tam giác ABM và tam giác ACM có:
AB = AC (chứng minh trên),
(do ∆ABC cân tại A),
BM = CM (do M là trung điểm BC)
Do đó ∆ABM = ∆ACM (c.g.c)
Suy ra (hai góc tương ứng)
Mà (hai góc kề bù)
Do đó
Suy ra AM ⊥ BC tại trung điểm M của BC
Khi đó AM là đường trung trực của BC (2)
Từ (1), (2), ta suy ra A, O, M thẳng hàng.
Do đó đáp án B đúng.
Ta có O thuộc AM (chứng minh trên).
Mà O là giao điểm của BE và CD.
Suy ra ba đường thẳng AM, BE, CD đồng quy tại điểm O.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
Đáp án đúng là: D
Ta có AB = AC (do ∆ABC cân tại A) và AD = AE (giả thiết).
Suy ra AB – AD = AC – AE.
Do đó BD = CE.
Xét ∆EBC và ∆DCB, có:
BC là cạnh chung.
(do ∆ABC cân tại A).
BD = CE (chứng minh trên).
Do đó ∆EBC = ∆DCB (c.g.c)
Suy ra (cặp góc tương ứng).
Suy ra ∆BOC cân tại O.
Do đó đáp án A đúng.
Ta có ∆BOC cân tại O.
Suy ra OB = OC.
Mà AB = AC (chứng minh trên)
Do đó AO là đường trung trực của cạnh BC (1).
Xét tam giác ABM và tam giác ACM có:
AB = AC (chứng minh trên),
(do ∆ABC cân tại A),
BM = CM (do M là trung điểm BC)
Do đó ∆ABM = ∆ACM (c.g.c)
Suy ra (hai góc tương ứng)
Mà (hai góc kề bù)
Do đó
Suy ra AM ⊥ BC tại trung điểm M của BC
Khi đó AM là đường trung trực của BC (2)
Từ (1), (2), ta suy ra A, O, M thẳng hàng.
Do đó đáp án B đúng.
Ta có O thuộc AM (chứng minh trên).
Mà O là giao điểm của BE và CD.
Suy ra ba đường thẳng AM, BE, CD đồng quy tại điểm O.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho ∆ABC có AB < AC. Trên cạnh AC lấy điểm M sao cho CM = AB. Vẽ đường trung trực của AC, cắt tia phân giác của tại điểm O. Đường trung trực của đoạn thẳng BM đi qua điểm:
Cho ∆ABC có AB < AC. Trên cạnh AC lấy điểm M sao cho CM = AB. Vẽ đường trung trực của AC, cắt tia phân giác của tại điểm O. Đường trung trực của đoạn thẳng BM đi qua điểm:
Câu 2:
Cho ∆ABC có ba góc nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối của tia OB, lấy điểm D sao cho OB = OD. Biết . Khẳng định nào sau đây đúng nhất?
Cho ∆ABC có ba góc nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối của tia OB, lấy điểm D sao cho OB = OD. Biết . Khẳng định nào sau đây đúng nhất?
Câu 3:
Cho , A là một điểm di động ở trong . Vẽ các điểm M và N sao cho Ox là đường trung trực của AM và Oy là đường trung trực của AN. Để O là trung điểm của MN của giá trị của α bằng:
Cho , A là một điểm di động ở trong . Vẽ các điểm M và N sao cho Ox là đường trung trực của AM và Oy là đường trung trực của AN. Để O là trung điểm của MN của giá trị của α bằng:
Câu 4:
Cho ∆ABC vuông tại A. Trên cạnh BC lấy điểm M bất kì. Vẽ các điểm D và E sao cho AB là đường trung trực của MD và AC là đường trung trực của ME. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC vuông tại A. Trên cạnh BC lấy điểm M bất kì. Vẽ các điểm D và E sao cho AB là đường trung trực của MD và AC là đường trung trực của ME. Khẳng định nào sau đây đúng nhất?
Câu 5:
Câu 6:
Cho ∆ABC cân tại A. Gọi M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại E. Điểm E thuộc đường thẳng nào trong các đường thẳng sau đây.
Cho ∆ABC cân tại A. Gọi M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại E. Điểm E thuộc đường thẳng nào trong các đường thẳng sau đây.
Câu 7:
Cho ∆ABC có là góc tù. Các đường trung trực của cạnh AB và AC cắt nhau tại O và cắt BC theo thứ tự tại D và E. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC có là góc tù. Các đường trung trực của cạnh AB và AC cắt nhau tại O và cắt BC theo thứ tự tại D và E. Khẳng định nào sau đây đúng nhất?
Câu 8:
Cho ∆ABC vuông tại A. Gọi E, F lần lượt là trung điểm các cạnh AC, AB. Giao điểm của ba đường trung trực của tam giác ABC:
Câu 9:
Cho ∆ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM = BN = CP. Giao điểm của ba đường trung trực của ∆MNP là
Câu 10:
Cho ∆ABC cân tại A, có . Đường trung trực của cạnh AB cắt BC tại D. Trên tia đối của tia AD, lấy điểm M sao cho AM = CD. Khẳng định nào sau đây đúng nhất?
Cho ∆ABC cân tại A, có . Đường trung trực của cạnh AB cắt BC tại D. Trên tia đối của tia AD, lấy điểm M sao cho AM = CD. Khẳng định nào sau đây đúng nhất?
Câu 11:
Cho ∆ABC có tù. Các đường trung trực của AB và AC cắt BC lần lượt tại D và E. Biết . Số đo bằng:
Cho ∆ABC có tù. Các đường trung trực của AB và AC cắt BC lần lượt tại D và E. Biết . Số đo bằng:
Câu 12:
Cho ∆ABC, gọi I là giao điểm của hai đường trung trực của hai cạnh AB và AC. Kết quả nào dưới đây đúng?
Cho ∆ABC, gọi I là giao điểm của hai đường trung trực của hai cạnh AB và AC. Kết quả nào dưới đây đúng?


