Cho a và b là các số nguyên dương thỏa mãn  $\underset{x\to 0}{\lim }\frac{e^{ax}-1}{\sin bx}=\frac{5}{3}$ .Tích ab có thể nhận giá trị bằng số nào trong các số dưới đây?

Tìm m để các hàm số  $f\left(x\right)=\left\{\begin{array}{l}\frac{\sqrt{x+1}-1}{x} khi x>0\\ 2x^2+3m+1 khi x\le 0\end{array}\right.$liên tục trên R.

Tìm a  để hàm số sau liên tục tại x = 0.

Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x^2-5x+6}{2x^3-16} khi x<2\\ 2-x khi x\ge 2\end{array}\right.$ Khẳng định nào sau đây đúng nhất.

Tìm khẳng định đúng trong các khẳng định sau:

 (I) $f\left(x\right)=\frac{\sqrt{x+1}}{x-1}$liên tục với mọi $x\ne$1

(II)  f(x) = sinx liên tục trên R.

(III)  $f\left(x\right)=\frac{\left|x\right|}{x}$liên tục tại x = 1

Cho hàm số $$\begin{gathered} f\left(x\right)=\left\{\begin{array}{l}{x}^2 , x\ge 1 \\ \frac{2x^3}{1+x} ,0\le x\le 1\\ x \sin x , x<0\end{array}\right. \end{gathered}$$Tìm khẳng định đúng trong các khẳng định sau:

Tìm a  để các hàm số $f\left(x\right)\left\{\begin{array}{l}\frac{\sqrt{3x+1}-2}{x^2-1} Khi x >1\\ \frac{a(x^2-2)}{x-3} Khi x\le 1\end{array}\right.$ liên tục tại x = 1

Tìm m để các hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{\sqrt[3]{x-2}+2x-1}{x-1},khi x khác 1\\ 3m-2 , khi x=1\end{array}\right.$liên tục trên R

Cho hàm số $$\begin{gathered} f\left(x\right)=\left\{\begin{array}{l}\frac{3-\sqrt{9-x}}{x} , 0<x<9 \\ m ,x=0\\ \frac{3}{x} ,x\ge 9\end{array}\right. \end{gathered}$$Tìm m  để f(x) liên tục trên [0; +∞) là.

Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}{a}^2{x}^2 , x\le \sqrt{2}, a\in \mathrm{ℝ}\\ (2-a)x^2 , x>\sqrt{2}\end{array}\right.$Giá trị của a  để f (x)  liên tục trên R  là:

Cho hàm số $f\left(x\right)=\frac{x^2+1}{x^2+5x+6}$ Khi đó hàm số y = f(x) liên tục trên các khoảng nào sau đây?

Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{ \tan x }{x}; x khác 0 \wedge x khác \frac{\mathrm{\pi }}{2}+k\mathrm{\pi }; \mathrm{k}\in \mathrm{\mathbb{Z}}\\ 0 ; x=0\end{array}\right.$Hàm số y = f(x) liên tục trên các khoảng nào sau đây?

Cho hàm số f(x) có đồ thị như hình dưới đây:

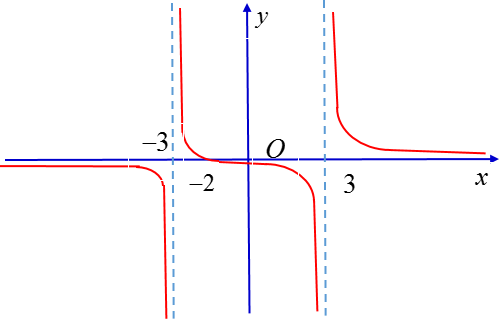
Quan sát đồ thị và cho biết trong các giới hạn sau, giới hạn nào là +∞ ?

Tìm khẳng định đúng trong các khẳng định sau:

$\mathbf{\left(}\mathbf{I}\mathbf{\right)}\mathbf{ }\mathrm{f}\left(\mathrm{x}\right) = \frac{1}{\sqrt{{\mathrm{x}}^2-1}}$ liên tục với mọi x.

$\mathbf{\left(}\mathbf{II}\mathbf{\right)} \mathrm{f}\left(\mathrm{x}\right)=\frac{\sin \mathrm{x} }{\mathrm{x}}$ có giới hạn khi x → 0.

$\mathbf{\left(}\mathbf{III}\mathbf{\right)}\mathbf{ }\mathrm{f}\left(\mathrm{x}\right)=\sqrt{9-{\mathrm{x}}^2}$ liên tục trên đoạn [-3; 3].

Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{x+1+\sqrt[3]{x-1}}{x} khi x khác 0\\ 2 khi x=0\end{array}\right.$ Khẳng định nào sau đây đúng nhất

Cho hàm số $f\left(x\right)=\left\{\begin{array}{l}\frac{\sqrt[3]{x}-1}{\sqrt{x}-1} khi x>1\\ \frac{\sqrt[]{1-x}+2}{x+2} khi x\le 1\end{array}\right.$Khẳng định nào sau đây đúng nhất.